目录
点积(dot product)
又叫标量积、数量积(scalar product)。它是两个数字序列的相应条目的乘积之和。在欧几里得几何中,两个向量的笛卡尔坐标的点积被广泛使用。它通常被称为欧几里得空间的内积(或很少称为投影积),是内积的一种特殊情况,尽管它不是可以在欧几里得空间上定义的唯一内积。
在代数上,点积是两个数字序列的相应条目的乘积之和。在几何上,它是两个向量的欧几里得大小和它们之间夹角的余弦的乘积。这两个定义在使用笛卡尔坐标时是等价的。在现代几何中,欧几里得空间通常使用向量空间来定义。在这种情况下,点积用于定义长度(向量的长度是向量本身的点积的平方根)和角度(两个向量夹角的余弦等于它们的点积与它们长度的乘积的商)。
代数定义

几何定义

与内积的关系

叉积(corss product)
或向量积(vector product )(有时是有向面积积,以强调其几何意义)是在三维有向欧几里得向量空间,并用符号x表示. 给定两个线性独立的向量 a和b,叉积a × b(读作“a cross b”)是一个垂直于a和b的向量,因此垂直于包含它们的平面。
定义

下图为使用 Sarrus 规则得到a和b的叉积

叉积也可以表示为形式行列式:
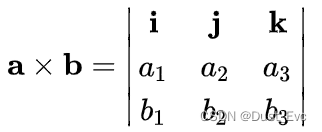
这个行列式可以使用Sarrus 规则或辅因子扩展来计算。使用 Sarrus 规则,它扩展为
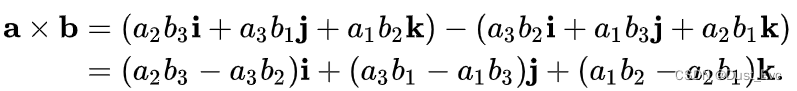
沿用第一行使用辅因子改为,它展开为
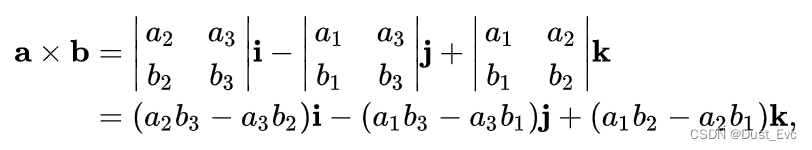
它直接给出了结果的分量。
几何意义

内积(inner product)
空间中两个向量的内积是一个标量,通常用尖括号表示,例如。内积空间推广了欧氏向量空间,在欧氏向量空间中内积是笛卡尔坐标的点积或标量积。
无穷维内积空间广泛用于泛函分析。复数域上的内积空间有时称为酉空间。具有内积的向量空间概念的第一次使用是由于朱塞佩·皮亚诺,1898 年。

使用内积定义的两个向量之间角度的几何解释( |x| 与 |y| 为范数在二维三维空间的表现)
定义

例子

外积(outer product)
在线性代数中,两个坐标向量的外积是一个矩阵。如果这两个向量的维度是n和m,那么它们的外积是一个n × m矩阵。更一般地说,给定两个张量(多维数字数组),它们的外积是张量。张量的外积也称为张量积,可用于定义张量代数。
定义

与欧几里得内积对比

张量的外积
