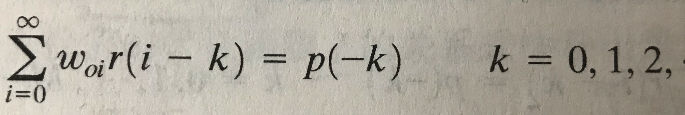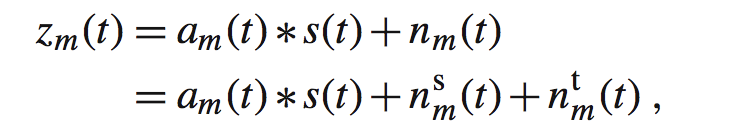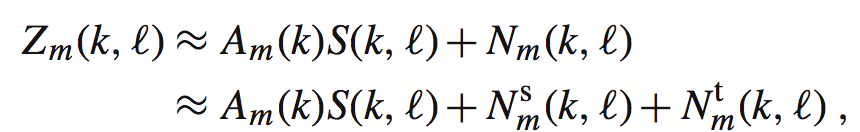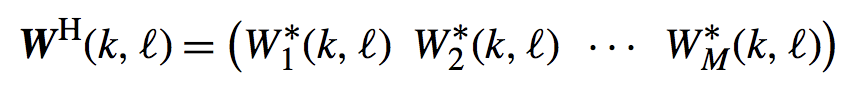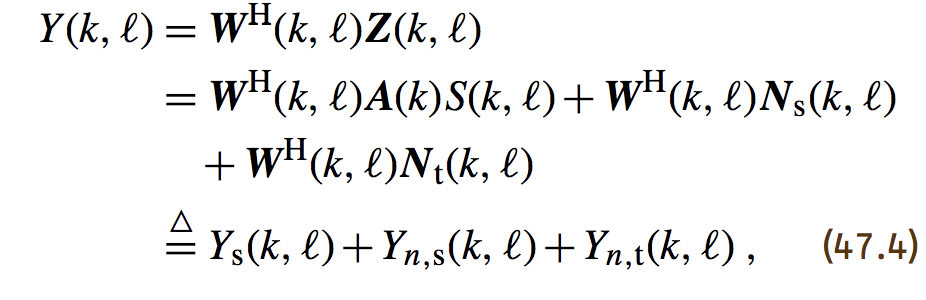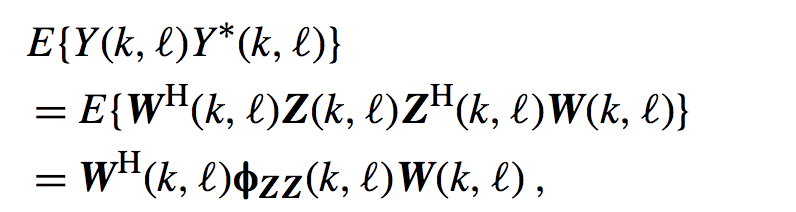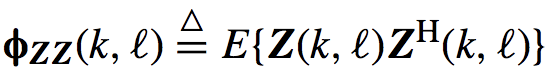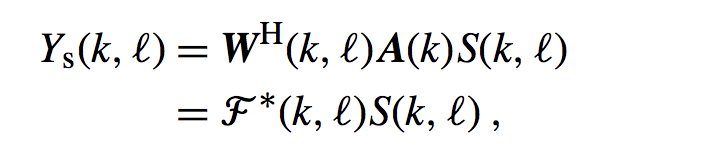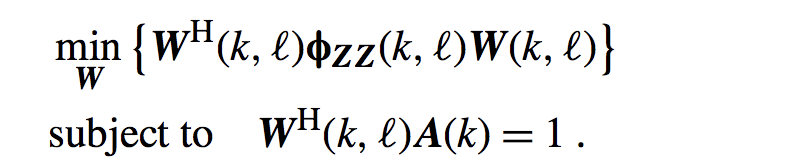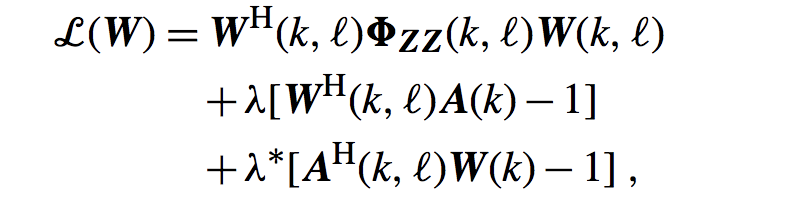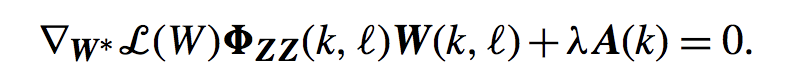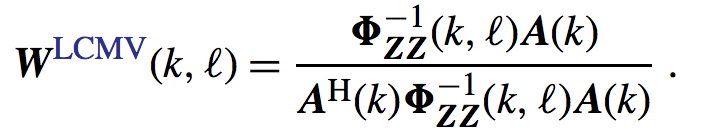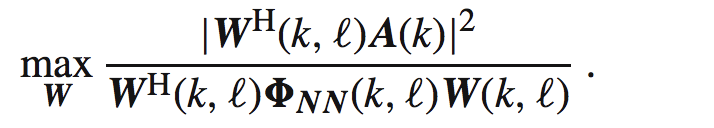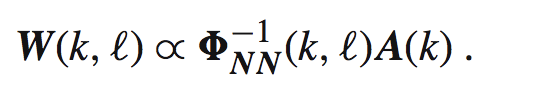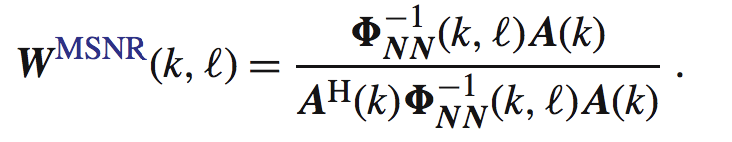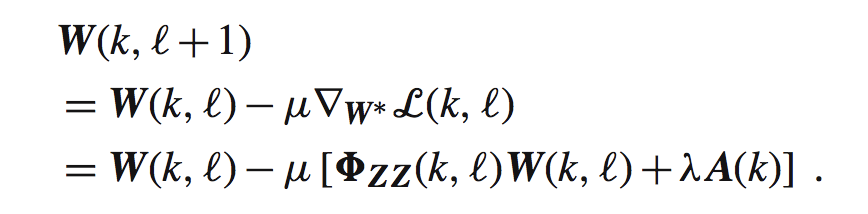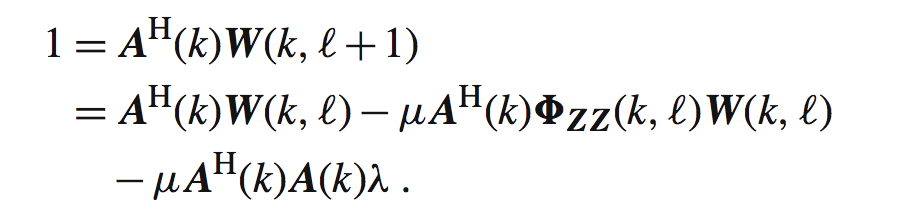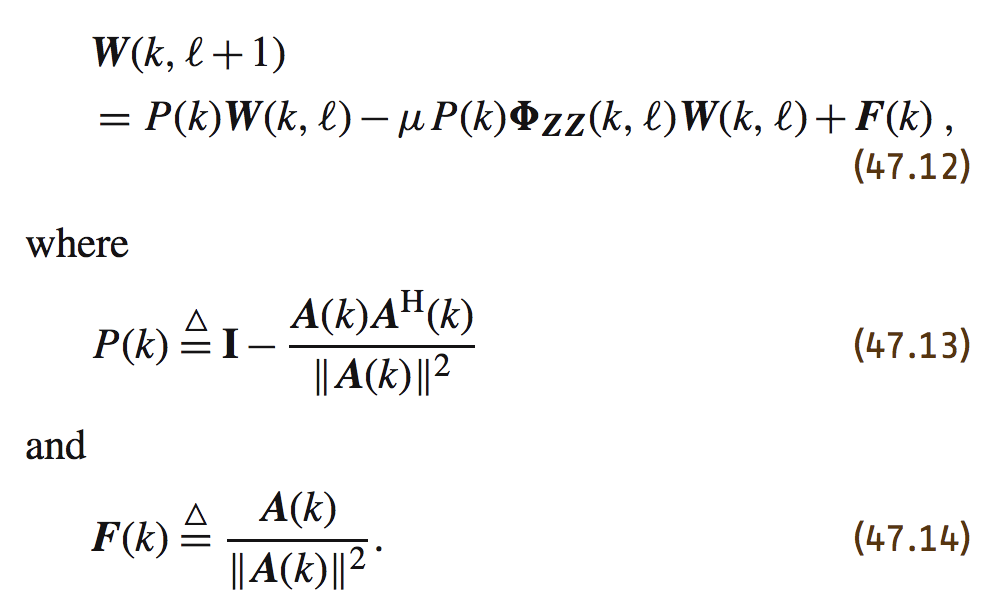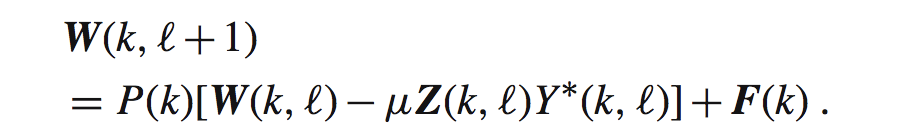今天准备总结一下LCMV算法的知识点,同时明后两天我会把算法转化为matlab代码如果时间来的及我会同时把效果测试的代码一同放入到我的github,至于地址见我的个人资料下面。不多说,进入LCMV算法。
在正是开始之前我要简要说一下LCMV算法,也可以称之为:constrained least mean square,约束最小均差。我之前写了两章有关于维纳滤波器的,那么这里有朋友可能会问:到底什么是维纳滤波器,他和我们经常用的LMS算法有什么区别?同学,这个问题很上路,老夫拼了这一身修为也要为你解答。
首先,什么是维纳滤波器?(因为前面讲过维纳滤波器,我会简要概括)我们假设代价函数为误差e(输入信号和期望响应的差值)的均方比如:E[|e^2|]。那么通过正交性原理我们知道,要使得代价函数获得最小值,我们的误差e与当前时刻的输入信号u成正交关系(比如两个垂直的向量想乘为0),通过这点我们能够推导出维纳霍夫方程,这个方程是维纳滤波器的灵魂。方程表明要求的最优(注意这个最优)的维纳滤波器必须要提前知道输入信号的自相关R和输入信号与期望响应的互相关p。下面是维纳霍夫方程:
转化成向量矩阵模式累加符号就消除了变为:R*W=P,为了求W我们就需要把两边同时乘以R的逆,然后就推到出来了。最终得到的关于权重的表达式就是我们的维纳滤波器,请记住上面我写的,这些都是细节,等会会与lms做比较。
那么现在我们面临一些问题:我们提前对于环境一无所知,不知道R,不知道P,R至少还能求解出来,那P可没法求呀。同时维纳滤波器中涉及R矩阵的求逆,玩过算法的都知道,求逆运算十分消耗资源的,当每变化一个W就需要求解逆运算,这样的计算复杂度相信许多应用都不能接受,所以你看到的很多资料上都这样描述维纳滤波器:不切实际,理论最优等等。科学家是伟大的,出了问题就会找解决方案,这时LMS算法浮出水面。
LMS算法核心思想就是迭代,他不需要提前知道任何关于环境的信息,也就是说他不需要知道R或者P,他是随机梯度算法的产物。为什么不需要R或者P了呢?因为它使用输入信号u和误差e的内积作为梯度向量的估计值,直接把R和P替换掉了,完美,甚至都不需要计算R的逆运算了。一次次迭代更新W权重的值,最终趋向于维纳最优解 。不过有个细节:因为我们是使用替换的方式,所以存在梯度噪声,所以我们最终的解是在维纳滤波器周围很小很小的区域动荡的。在误差性能曲面上,就是在最低点左右跳动。当输入信号能量很大的时候,梯度噪声也随之变大,这也是为什么引入NLMS,进行归一化操作,这个暂且不谈,这样我们对于维纳滤波器和LMS算法的联系和区别也算是有了大概的了解,那么我们下面开始进入LCMV算法,ShowTime。
问题公式化
试想一下这种环境:把包含M个麦克风的阵列置于一个嘈杂和带有混响的环境里。我们接收到的信号一般包含三部分:第一部分是期望信号,第二部分是一些稳态的干扰信号,第三部分是非稳态的噪声部分。我们的目的是从接收到的信号中重塑语音部分。我们假设s(t)表示期望信号,am(t)表示第m个麦克风到期望信号源的RIR(房间冲激响应),nm(t)表示在第m个麦克风上的噪声部分。那么我们在第m个麦克风上接收到的信号如下:
第二个等号第二和第三项分别代表第m个麦克风稳态和非稳态的噪声,同时*表示卷积,至于为什么这里使用卷积,因为我们考虑混响。我们假设两个噪声分量可能包含相干噪声分量和扩散噪声分量。
那么我们现在开始对数据进行分帧操作,同时对每帧应用窗函数后进行快速傅立叶变换(STFT)。假设我们的传递函数是时不变的,那么我们得到时-频域如下:
这里的l是帧的索引(也就是第几帧),k表示频率块的索引。这里有个细节,我们的块长度在理论上要长于RIR,不过由于RIR一般非常长,我们不一定能够精确匹配,所以二者至少应当大致相似。其余大写字母都是对应信号的STFT变换。Am(k)是关于声源到第m个麦克风的ATF(acoustic transfer function)。我们把上面的式子写成向量形式如下:
其中:
到此为止,我们把问题公式化完毕。(记住,一般看英文论文时,第二节一般都会时问题描述并公式化,要熟悉这个套路,这个也就是对问题进行建模)
自适应波束形成器
Frost提出了一种波束形成滤波器,这种滤波器假设:声源到不同的麦克风之间的ATF仅仅是由增益和延迟决定的。这也是最简单的一种假设,这种假设一般实现容易,不过对于具有混响的能力十分有限,不过作为MVDR和GSC波束形成器一脉的鼻祖,我们更多的学习一下他的思想。接下来,我们会得到一个频域的Frost算法,此算法针对任意ATF情况(其实原文中的这个任意很有喜感)。我们首先会得到一个封闭形式的LCMV波束形成器,然后推到出他的自适应解。最终的结果是约束LMS类型的算法。如果日后有机会,我会把基于LCMV的GSC和MVDR也讲解一遍。
频域LCMV算法
最优解(维纳解)
如下定一个M个滤波器:
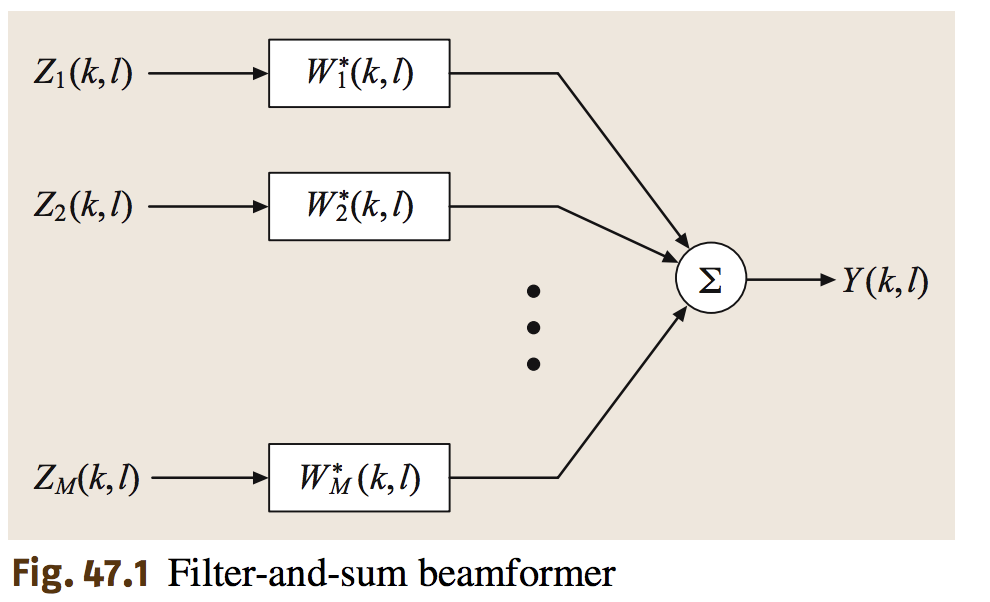
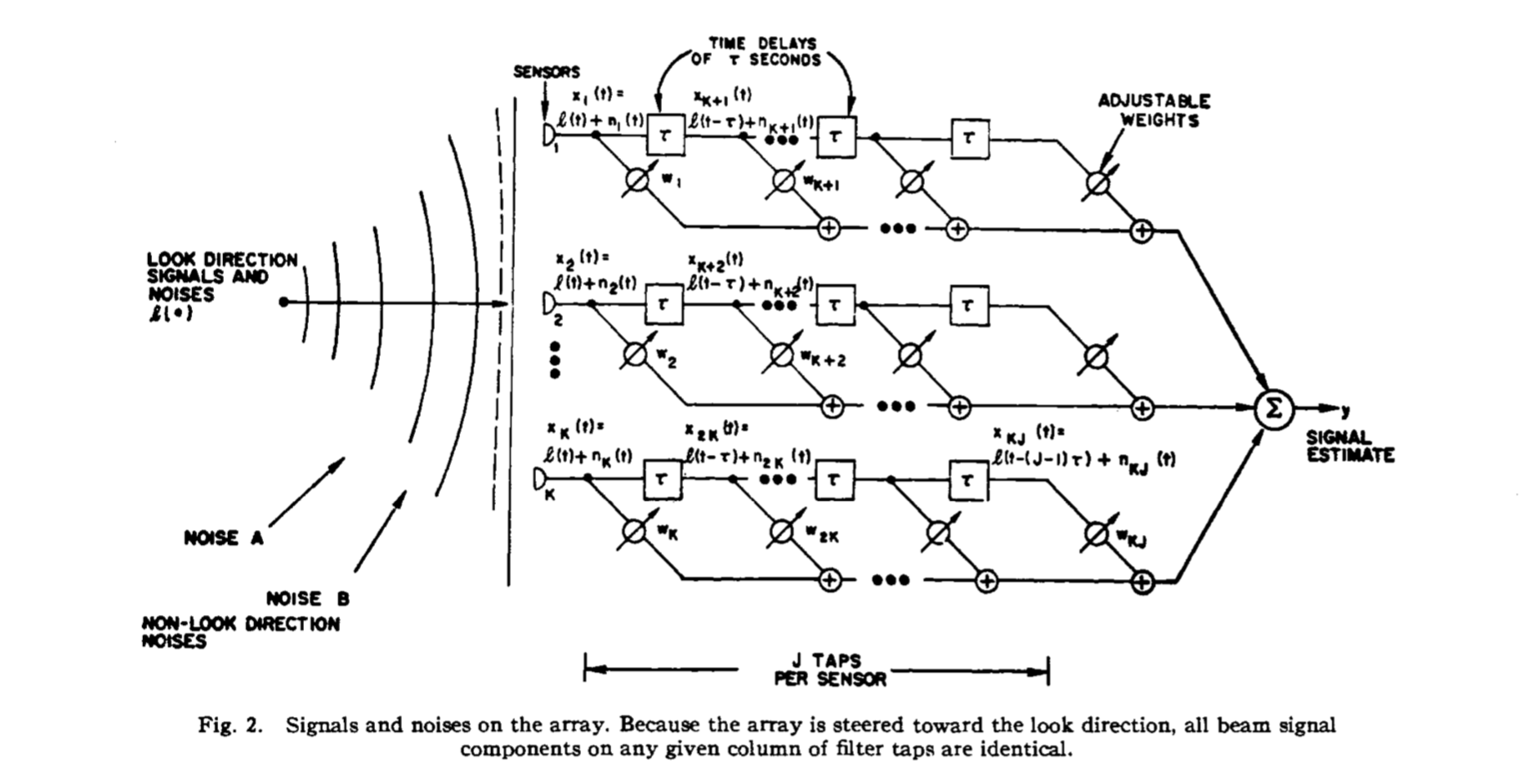
其中的H表示转置共轭的意思。filter-sum的波束形成器如下图:
这个就相当于我们对每个麦克风接受到的信号进行滤波器然后把结果相加,用公式表达如下:
这里的Ys(k,l)是期望信号部分,而Yn,s(k,l)和Yn,t(k,l)是稳态和非稳态噪声部分。我们波束形成器的输出功率为:
其中:
他是关于接收到信号的功率谱密度矩阵,你可以认为是频域的自相关函数,有些人问这不是协方差吗,怎么变成自相关了?假设方差为1均值为0,协方差和相关函数的公式是相同的,不要弄混,不过这里怎么叫都不错。下面进入我们的关键:下面给出一个约束:
F一般都是预先定义的滤波器,比如简单的延迟滤波器,我们一般假设为F(k,l)=1,也就是增强垂直方向信号(这里涉及较多内容,自己查阅空间滤波器和麦克风阵列等内容)。我们期望在这个约束的情况下,让输出的功率达到最小,这,就是我们算法要努力的方向。可能有人有疑问,为啥在此约束情况下让输出功率达到最小就能达到我们的目的?这个可以从两方面解释:一方面是从理论上,我们假设给的约束是包含空间的,比如你知道说话人在30度方向上(坐标系自己定义),那么你的约束是在30度方向的信号不减弱,比如为1不变。那么在此情况下降低整体输出功率其实就是在削弱噪声信号。一方面是从图形上,这种方法需要参考Frost的论文原文《An Algorithm for Linearly Constrained Adaptive Array Processing》,我们看如下的图片:
假设我们的约束条件定位与麦克风垂直方向入射的信号为期望信号方向,噪声从其他方向射来,那么同一时刻,我们以第一列tap值为例,分别为:x1(t)=l(t)+n1(t),x2(t)=l(t)+n2(t).....xk(t)=l(t)+nk(t),这里的l为期望信号,n为噪声。对此时刻此列taps的值进行相关运算如下(以x1和x2为例):
统计如上所述,我们最终的最小化问题变为了:
该最小化问题可以由下面的图来刻画:
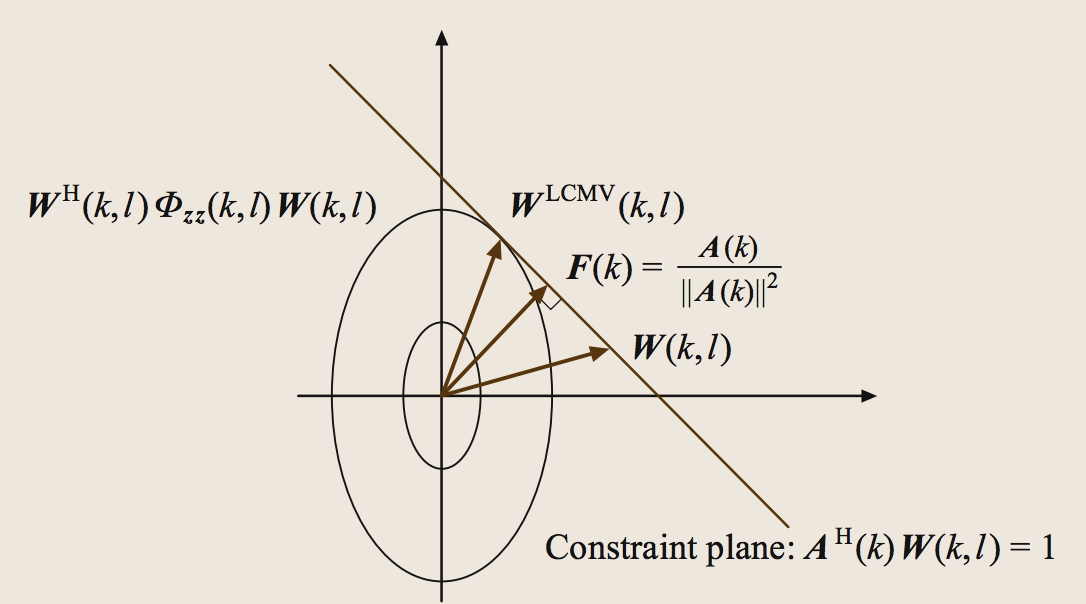
这里得好好解释一下这个图,以后要讲的GSC算法等都是基于这个图来的,我会按照我自己的理解来解释,如果有人不认同,可以在下面的评论区写上自己的想法,欢迎指正。不多说,我们开始。
首先建立一个坐标系(不要考虑细节比如怎么建立,实坐标系还是复坐标系,放过你自己,就一个坐标系,剩下你啥也不知道),我们能通过W^H(k,l)faizz(k,l)W(k,l)画出一个圆(你说椭圆也行,别钻到细节)。同理我们根据约束矩阵A^H(k)W(k,l)能画出一个约束平面(之所以说平面因为我们从一开始就没定义这是二维坐标系,所以这条直线可能是多维的)。如果我们要达到最优,就必须从圆上找到一个点满足约束平面,那么说白了就是二者的切点,这个点就是最优解,就是上面的 W^LCMV(k,l)。不过后面会讲,我们使用递归的方法从下面逼近这个最优点,这里不细说,记住刚才的内容即可。
很多朋友都知道,要计算在某种条件下的表达式,最常用的就是拉格朗日乘子法,具体不多讲,自己可以维基百科(求你了别去百度,百度百科真的胡乱贴,去维基,了解生命奥义)。那么我们定义复数拉格朗日乘子法如下:
式子中那个唯一你不认识不知道咋读的字母就是拉格朗日乘子(他叫lamada,和上面我用的fai都是希腊字母)。接下来就是让上面的式子对W*求导然后让导数为0得到极值点:
带入上面我们得到的式子,可以得到最优LCMV滤波器:
这就是封闭形式的LCMV,不过对于时变的环境很难实现,因为涉及相关矩阵的求逆,时间和资源消耗巨大,所以这就是一个理论的最优解,我们下面要把自适应算法应用此算法上,来解决上述问题。
这里有个比较有意思的事:LCMV的算法解与MSNR的解等价(后者我认为就是最大信噪比,用的代价函数可能不同),后者代价函数如下:
MSNR算法的解是适配滤波器:
如果我们给定约束为W^H(k,l)A(k)=1,我们能够得到在目标方向的信号无失真的情况下:
从这里可以看出来,二者等价。不过此等价仅仅对于ATF已知的情况下,如果ATF未知,二者是不同的。同时注意,因为非稳态噪声依赖于时间帧,所以时间依赖是导致波束形成器效果差的主要因素。此问题可以被后滤波器所解决。
自适应方法
我们上面说了,由于封闭式方法不可用,我们要把自适应的方法引入到lcmv算法中。
我们考虑如下的最速下降自适应算法:
我们把指向约束带入到W(l+1,k)产生如下式子:
这里能求出拉格朗日乘子lamada的表达式,然后带入上面的更新W的式子中,我们可以得到如下的式子:
其实这里书中没有讲,不过原文论文中讲了,这里的P其实是一个映射,把结果映射到约束平面上,F是我们之前图片的垂直的部分。所以当我们的权重一开始为0的时候,更新是从F开始的,从图形上来看是合理的,因为从F开始逼近W^LCMV能减少很多运算,这里其实有许多细节,包括p的用法,这里不一一介绍,有兴趣的可以去查看论文。
最终我们可以得到如下更新:
整个LCMV算法到此可以说介绍完毕,明后天我会开始把matlab代码写出来,然后附上测试放在我的github上,感兴趣的可以去看看。