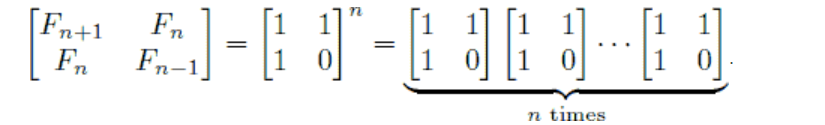斐波那契数列的第n项（矩阵快速幂）

矩阵快速幂是用来求解递推式的，所以第一步先要列出递推式:

 f(n)=f(n-1)+f(n-2)

第二步是建立矩阵递推式，找到转移矩阵:

,简写成T * A(n-1)=A(n)，T矩阵就是那个2*2的常数矩阵，而

这里就是个矩阵乘法等式左边:1*f(n-1)+1*f(n-2)=f(n);1*f(n-1)+0*f(n-2)=f(n-1);

所以这里相乘就是矩阵n-1次相乘,然后输出第一行第二个元素,也就是a[0][1]；

把第一个矩阵设为A，第二个矩阵设为B，第三个矩阵设为C。

（上述借鉴一位博主的，博客文章链接）

将上述的右乘矩阵中的f（n-1）和f（n-2）改为由f(n)和f(n-1)构成的矩阵，则两矩阵相乘后得到一个由f(n+1)和f(n)构成的矩阵,此时输出的为a[1][0]。

矩阵快速幂公式：

由 F2  F1  F1 F0   组成的矩阵的n次方  的左下角就是Fn。

更多矩阵乘法与矩阵快速幂的代码实现及解析请参考上一篇文章（文章链接）

1242 斐波那契数列的第N项 

基准时间限制：1 秒 空间限制：131072 KB 分值: 0 难度：基础题

 收藏

 关注

斐波那契数列的定义如下：

F(0) = 0

F(1) = 1

F(n) = F(n - 1) + F(n - 2) (n >= 2)

(1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, ...)

给出n，求F(n)，由于结果很大，输出F(n) % 1000000009的结果即可。

Input

输入1个数n(1 <= n <= 10^18)。

Output

输出F(n) % 1000000009的结果。

Input示例

11

Output示例

89

代码实现（题目链接）：

#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
typedef long long ll;
const int mod=1e9+9;
const int N=2;
ll tmp[N][N],res[N][N];
void multi(ll a[][N],ll b[][N],int n)
{
    memset(tmp,0,sizeof(tmp));
    for(ll i=0;i<n;i++)
    {
	   for(ll j=0;j<n;j++)
	   {
        for(ll k=0;k<n;k++)
        {
        tmp[i][j]+=(a[i][k]*b[k][j])%mod;
        }
        tmp[i][j]=tmp[i][j]%mod;
      }
   }
    for(ll i=0;i<n;i++)
        for(ll j=0;j<n;j++)
        a[i][j]=tmp[i][j];
}
void Pow(ll a[][N],ll m,int n)
{
    memset(res,0,sizeof(res));//m是幂，n是矩阵大小
    for(ll i=0;i<n;i++) res[i][i]=1;
    while(m)
    {
	    if(m&1)
        multi(res,a,n);//res=res*a;复制直接在multi里面实现了；
        multi(a,a,n);//a=a*a
        m>>=1;
    }
}
int main()
{
     ll m;
     int n;
     ll a[N][N]; 
    while(~scanf("%lld",&m)) 
    {  
         n=2;
    	a[0][0]=1,a[0][1]=1,a[1][0]=1,a[1][1]=0;
		Pow(a,m,n);
 	   printf("%lld\n",res[1][0]);
	}		
   return 0;
}