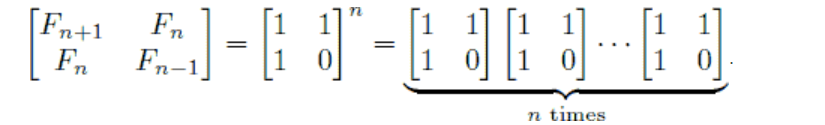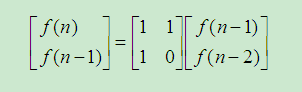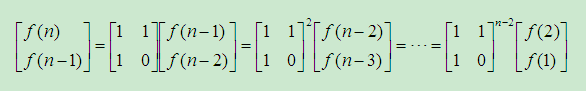斐波那契数列的第N项 51Nod - 1242(矩阵快速幂)

斐波那契数列的定义如下：

F(0) = 0

F(1) = 1

F(n) = F(n - 1) + F(n - 2) (n >= 2)

(1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, ...)

给出n，求F(n)，由于结果很大，输出F(n) % 1000000009的结果即可。

Input

输入1个数n(1 <= n <= 10^18)。

Output

输出F(n) % 1000000009的结果。

Sample Input
11
Sample Output
89

题目大意：就是求斐波那契的第n项。

解题思路：矩阵快速幂。

将上述的右乘矩阵中的f（n-1）和f（n-2）改为由f(n)和f(n-1)构成的矩阵，则两矩阵相乘后得到一个由f(n+1)和f(n)构成的矩阵,此时输出的为a[1][0]。

/*
@Author: Top_Spirit
@Language: C++
*/
//#include <bits/stdc++.h>
#include <iostream>
#include <cmath>
using namespace std ;
typedef long long ll ;
const int Maxn = 2 ;
const int MOD = 1e9 + 9 ;

#define mod(x) ((x) % MOD)

struct mat{
    ll m[Maxn][Maxn] ;
}unit;

mat operator * (mat a, mat b){
    mat ret  ;
    ll x ;
    for (ll i = 0;i < 2; i++){
        for (ll j = 0; j < 2; j++){
            x = 0 ;
            for (ll k = 0; k < 2; k++){
                x += mod(ll (a.m[i][k] * b.m[k][j])) ;
            }
            ret.m[i][j] = mod(x) ;
        }
    }
    return ret ;
}

void init_unit(){
    for (ll i = 0; i < Maxn; i++){
        unit.m[i][i] = 1 ;
    }
    return ;
}

mat pow_mat(mat a, ll n){
    mat ret = unit ;
    while (n){
        if (n & 1) ret = ret * a ;
        a = a * a ;
        n >>= 1 ;
    }
    return ret ;
}

int main (){
    ll x ;
    init_unit() ;
    while (cin >> x){
        mat a ;
    	a.m[0][0] = 1, a.m[0][1] = 1, a.m[1][0] = 1, a.m[1][1] = 0;
        mat ans = pow_mat(a, x) ;
        cout << ans.m[1][0]<< endl ;
    }
    return 0 ;
}

1.求第n项斐波那契数

　　根据斐波那契数的定义 F0 = 0，F1 = 1;

　　　　　　　　　 Fn = Fn - 1 + Fn - 2（n>=2）.

　　可以用矩阵表示为：

　进一步递推得到：

这里需要求的是右边系数矩阵的n-2次幂，然后代入前两项即可求得f(n)，也就是第n项斐波那契数。

/*
@Author: Top_Spirit
@Language: C++
*/
//#include <bits/stdc++.h>
#include <iostream>
#include <cmath>
using namespace std ;
typedef long long ll ;
const int Maxn = 2 ;
const int MOD = 1e9 + 9 ;

#define mod(x) ((x) % MOD)

struct mat{
    ll m[Maxn][Maxn] ;
}unit;

mat operator * (mat a, mat b){
    mat ret  ;
    ll x ;
    for (ll i = 0;i < 2; i++){
        for (ll j = 0; j < 2; j++){
            x = 0 ;
            for (ll k = 0; k < 2; k++){
                x += mod(ll (a.m[i][k] * b.m[k][j])) ;
            }
            ret.m[i][j] = mod(x) ;
        }
    }
    return ret ;
}

void init_unit(){
    for (ll i = 0; i < Maxn; i++){
        unit.m[i][i] = 1 ;
    }
    return ;
}

mat pow_mat(mat a, ll n){
    mat ret = unit ;
    while (n){
        if (n & 1) ret = ret * a ;
        a = a * a ;
        n >>= 1 ;
    }
    return ret ;
}

int main (){
    ll x ;
    init_unit() ;
    while (cin >> x){
        mat a ;
    	a.m[0][0] = 1, a.m[0][1] = 1, a.m[1][0] = 1, a.m[1][1] = 0;
        mat ans = pow_mat(a, x - 2) ;
        mat tmp ;
        tmp.m[0][0] = 1, tmp.m[1][0] = 1, tmp.m[0][1] = 0, tmp.m[1][1] = 0 ;
        ans = ans * tmp ;
        cout << ans.m[0][0]<< endl ;
    }
    return 0 ;
}

斐波那契数列的第N项 51Nod - 1242(矩阵快速幂)

猜你喜欢