对应分析( correspondence analysis )是在R型和Q型因子分析基础上发展起来的多元统计分析方法,又称为R-Q型因子分析。
例 试用对应分析研究我国部分省份的农村居民家庭人均消费支出结构。选取7个变量:A为食品支出比重,B为衣着支出比重,C为居住支出比重,D为家庭设备及服务支出比重,E为医疗保健支出比重,F为交通和通讯支出比重,G为文教娱乐、日用品及服务支出比重。考察的地区(即样品)有10个:山西、内蒙古、吉林、辽宁、黑龙江、海南、四川、贵州、甘肃、青海(原始数据见表1)。
表1 中国10个省份农村居民家庭人均消费支出数据
| 地区 |
A |
B |
C |
D |
E |
F |
G |
| 1山西 |
0.583910 |
0.111480 |
0.092473 |
0.050073 |
0.038193 |
0.018803 |
0.079946 |
| 2内蒙古 |
0.581218 |
0.081315 |
0.112380 |
0.042396 |
0.043280 |
0.040004 |
0.083339 |
| 3辽宁 |
0.565036 |
0.100121 |
0.123970 |
0.041121 |
0.043429 |
0.031328 |
0.078919 |
| 4吉林 |
0.530918 |
0.105360 |
0.116952 |
0.045064 |
0.043735 |
0.038508 |
0.095256 |
| 5黑龙江 |
0.555201 |
0.096500 |
0.143498 |
0.037566 |
0.052111 |
0.026267 |
0.072829 |
| 6海南 |
0.654952 |
0.047852 |
0.095238 |
0.047945 |
0.022134 |
0.018519 |
0.096844 |
| 7四川 |
0.640012 |
0.061680 |
0.116677 |
0.048471 |
0.033529 |
0.017439 |
0.072043 |
| 8贵州 |
0.725239 |
0.056362 |
0.073262 |
0.044388 |
0.016366 |
0.015720 |
0.057261 |
| 9甘肃 |
0.678630 |
0.058043 |
0.088316 |
0.038100 |
0.039794 |
0.015167 |
0.067999 |
| 1青海 |
0.665913 |
0.088508 |
0.096899 |
0.038191 |
0.039275 |
0.019243 |
0.033801 |
数据表41中列变量(A,B,C,D,E,F,G)是消费支出的几个指标,可以理解为属性变量“消费支出”的几个水平(或类目)。表41中的样品(行变量)是几个不同的地区,可理解为属性变量“地区”的几个不同水平(或类目)。
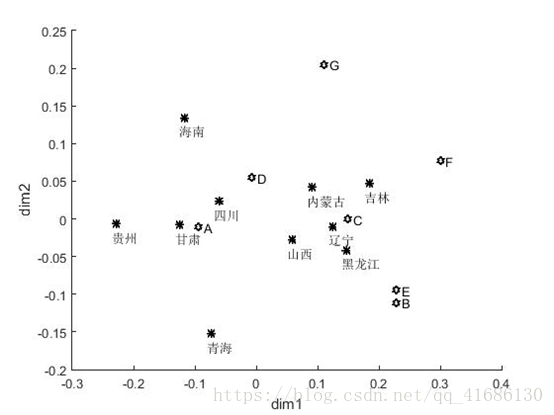
表2和图1给出了计算的主要结果。
表2 惯量和 (卡方)分解
| 奇异值 |
主惯量 |
卡方 |
贡献率 |
累积贡献率 |
| 0.13161 |
0.017321 |
0.170306 |
0.655946 |
0.655946 |
| 0.069681 |
0.004855 |
0.04774 |
0.183872 |
0.839818 |
| 0.048169 |
0.00232 |
0.022814 |
0.087868 |
0.927686 |
| 0.035818 |
0.001283 |
0.012614 |
0.048585 |
0.976271 |
| 0.022939 |
0.000526 |
0.005174 |
0.019927 |
0.996198 |
| 0.01002 |
0.0001 |
0.000987 |
0.003802 |
1 |
总 统计量等于0.2596,总 统计量的83.98%可用前两维即可说明,它表示行点和列点之间的关系用二维表示就足够了。
在图1中,给出10个样品点(用1,2,…,10表示)和7个变量点(用A,B,…,G表示)在相同坐标系上绘制的散布图。从图中可以看出,样品点和变量点可以分为两类;第一类包括变量点B,C,E,F,G和样品点1,2,3,4,5;第二类包括变量点A,D和样品点6,7,8,9, 10。
在第一类中,变量为衣着(B),居住(C),医疗保健(E),交通和通讯(F), 文教娱乐、日用品及服务(G)的支出分别占总支出的比重;地区有:山西(1),内蒙 古(2),辽宁(3),吉林(4),黑龙江(5),它们位于我国的东部和北部地区,说 明这5个地区的消费支出结构相似。在第二类中,变量为食品(A),家庭设备及服务(D) 的支出分别占总支出的比重;地区有:海南(6),四川(7),贵州(8),甘肃(9),青海(10),它们位于我国的南部和西部地区,说明这5个地区的消费支出结构相似。
MATLAB源代码:
clc, clear
a=load('xf.txt'); %原始文件保存在纯文本文件xf.txt中
T=sum(sum(a));
P=a/T; %计算对应矩阵P
r=sum(P,2); c=sum(P); %计算边缘分布
Row_prifile=a./repmat(sum(a,2),1,size(a,2)); %计算行轮廓分布阵
B=(P-r*c)./sqrt((r*c)); %计算标准化数据B
[u,s,v]= svd(B,'econ'); %对标准化后的数据阵B作奇异值分解
d=diag(s);
fprintf('奇异值为:\n');
disp(d);
w1=sign(repmat(sum(v),size(v,1),1)); %修改特征向量的符号矩阵,使得v中的每一个列向量的分量和大于0
w2=sign(repmat(sum(v),size(u,1),1)); %根据v对应地修改u的符号
vb=v.*w1; %修改特征向量的正负号
ub=u.*w2; %修改特征向量的正负号,本例中样本点个数和变量个数不等
lamda=diag(s).^2; %计算Z'*Z的特征值,即计算主惯量
fprintf('主惯量为:\n');
disp(lamda);
ksi2square=T*(lamda); %计算卡方统计量的分解
fprintf('卡方为:\n');
disp(ksi2square);
T_ksi2square=sum(ksi2square); %计算总卡方统计量
fprintf('总卡方统计量为:\n');
disp(T_ksi2square);
con_rate=lamda/sum(lamda); %计算贡献率
cum_rate=cumsum(con_rate); %计算累积贡献率
fprintf('累积贡献率为:\n');
disp(cum_rate);
beta=diag(r.^(-1/2))*ub; %求加权特征向量
G=beta*s; %求行轮廓坐标
alpha=diag(c.^(-1/2))*vb; %求加权特征向量
F=alpha*s; %求列轮廓坐标F
num1=size(G,1); %样本点的个数
rang=minmax(G(:,[1,2])'); %坐标的取值范围
delta=(rang(:,2)-rang(:,1))/(5*num1); %画图的标注位置调整量
ch={'A', 'B', 'C', 'D', 'E', 'F', 'G'};
yb={'山西','内蒙古','辽宁','吉林','黑龙江','海南','四川','贵州','甘肃','青海'};
hold on
plot(G(:,1),G(:,2),'*','Color','k','LineWidth',1.3) %画行点散布图
text(G(:,1)-delta(1),G(:,2)-3*delta(2),yb) %对行点进行标注
plot(F(:,1),F(:,2),'H','Color','k','LineWidth',1.3) %画列点散布图
text(F(:,1)+delta(1),F(:,2),ch) %对列点进行标注
xlabel('dim1'), ylabel('dim2')
xlswrite('tt',[diag(s),lamda,ksi2square,con_rate,cum_rate])
%把计算结果输出到Excel文件,这样便于把数据直接贴到word中的表格
ind1=find(G(:,1)>0); %根据行坐标第一维进行分类
rowclass=yb(ind1); %提出第一类样本点
ind2=find(F(:,1)>0); %根据列坐标第一维进行分类
colclass=ch(ind2); %提出第一类变量
fprintf('第一类样本及变量:\n');
disp(rowclass);
fprintf('\n')
disp(colclass);