梯度下降法
-
梯度下降法不是一个机器学习算法
-
是一种基于搜索的最优化方法(优化目标函数)
-
作用:最小化一个损失函数
-
梯度上升法:最大化一个效用函数
-
在求解机器学习算法的模型参数,即无约束优化问题时, 梯度下降(Gradient Descent)是最常采用的方法之一, 另一种常用的方法是最小二乘法
梯度下降法简介
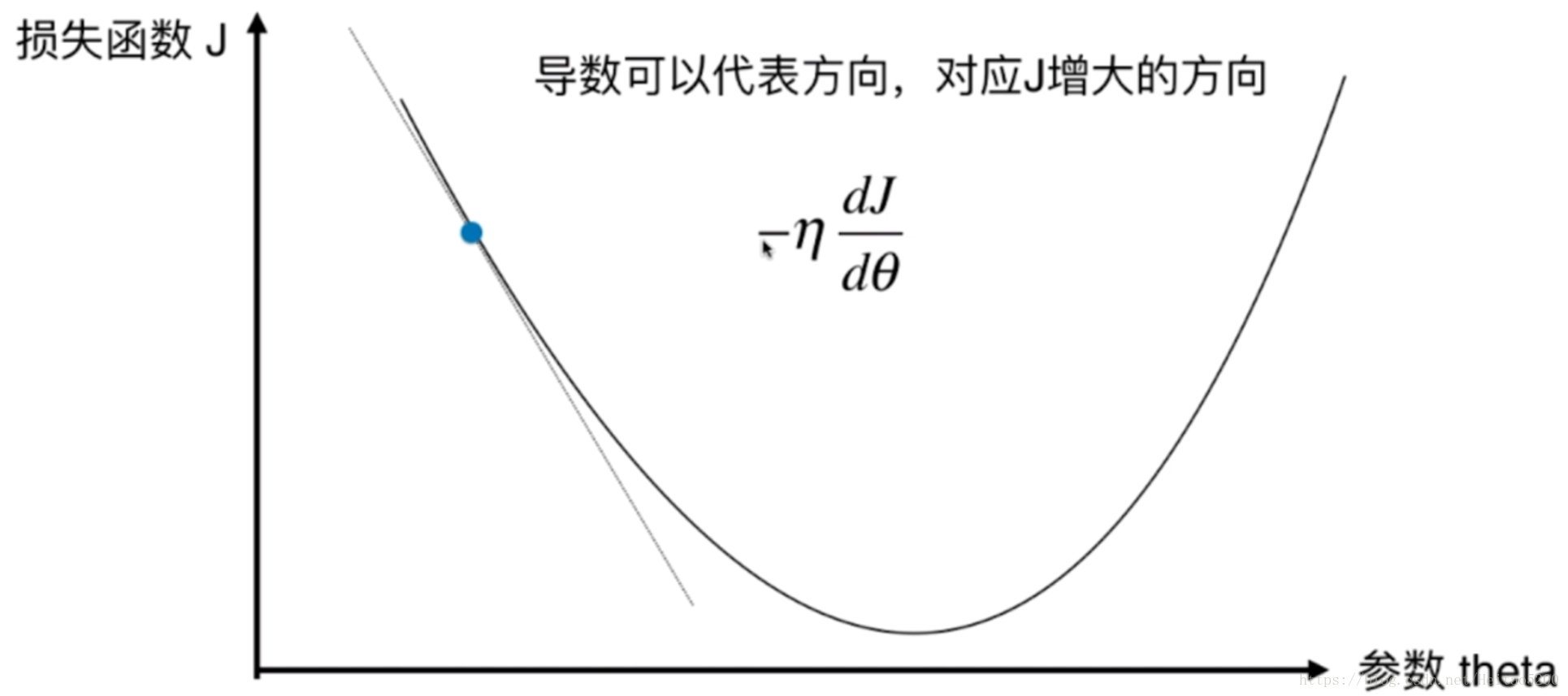
以下是定义了一个损失函数以后,参数 theta 对应的损失函数 J 的值对应的示例图, 我们需要找到使得损失函数值 J 取得最小值对应的 theta(这里是二维平面,也就是说数据集的特征只有一个), 在直线方程中,导数代表斜率; 在曲线方程中,导数代表切线斜率。这里导数即为梯度。
称为学习率,它是梯度下降法的一个超参数,它的取值反映获得最优解的速度,取值不合适时甚至得不到最优解。
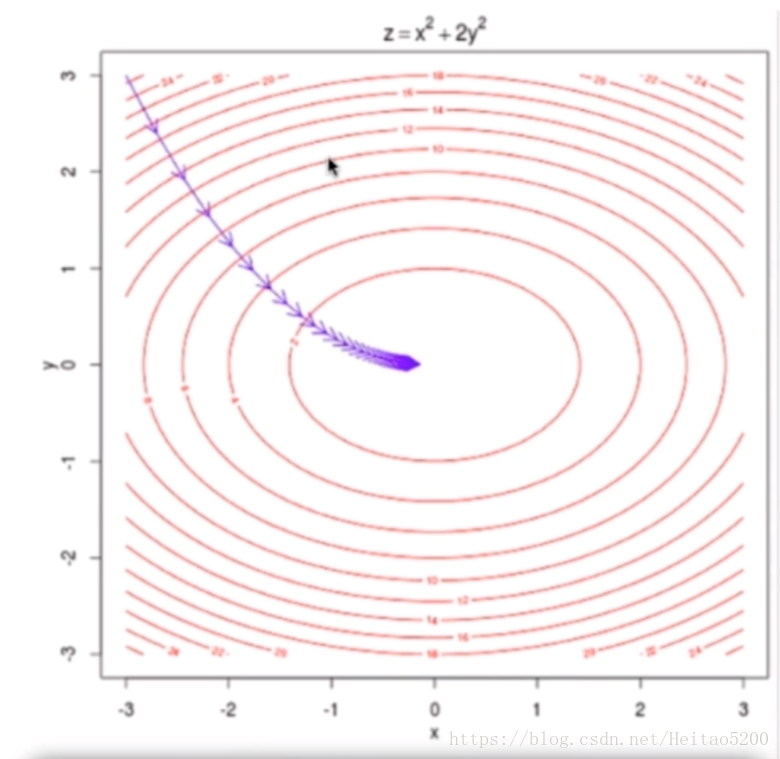
在三维平面,数据集的特征有两个的情况:

注意
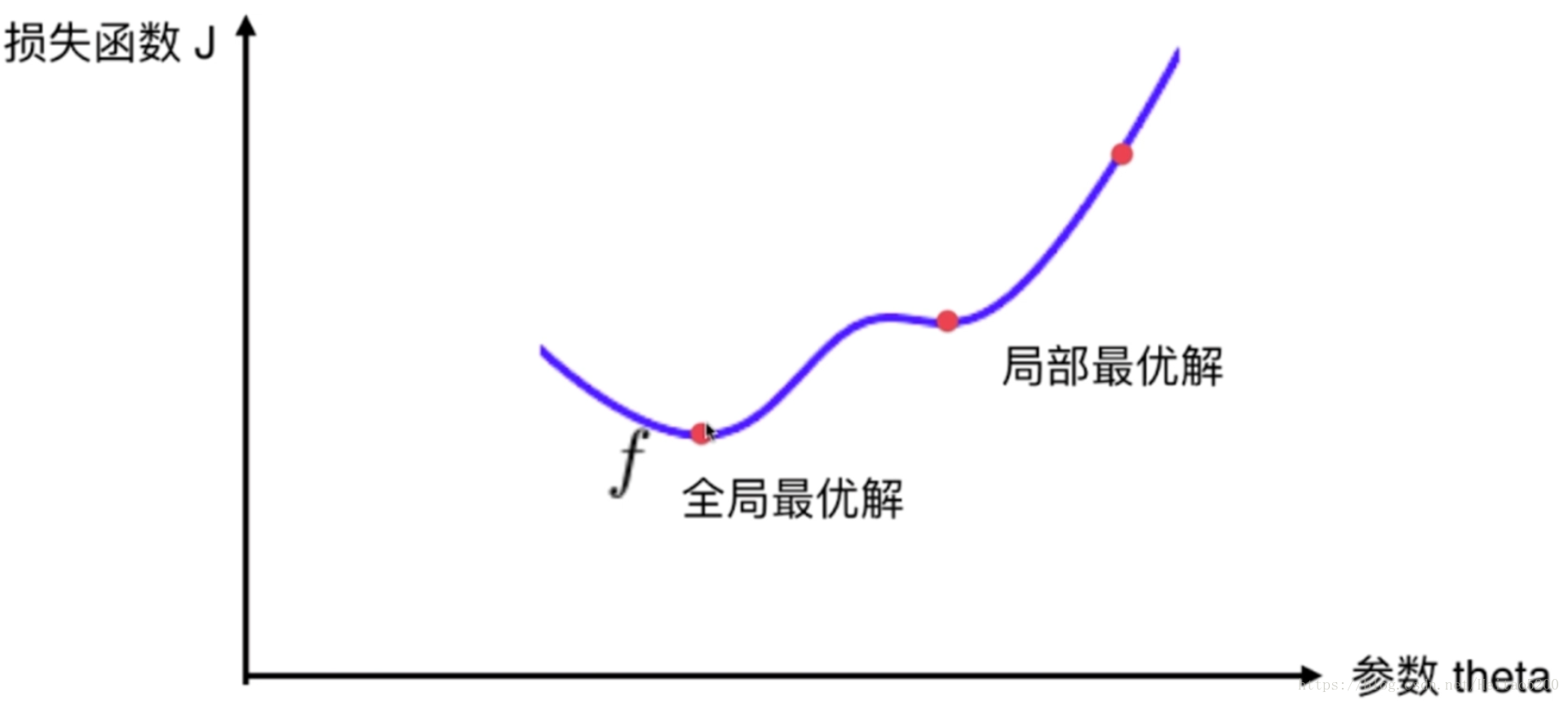
并不是所有的损失函数用梯度下降法都能够找到全局的最优解,有可能是一个局部最优解。 当然,如果损失函数是凸函数,梯度下降法得到的解就一定是全局最优解。
解决方案
-
多次运行,随机化初始点
-
梯度下降法的初始点也是一个超参数
-
设置合适的学习率。一般为0.01
梯度下降法求解(使损失函数尽可能小)
数据集处理
每个样本增加一个特征 $$x_0 =1$$
$$ \begin{pmatrix}
&(x_1^0) &(x_2^0) &\cdots &(x_4^0) &(y^0)\\
&(x_1^1) &(x_2^1) &\cdots &(x_4^1) &(y^1)\\
& \cdots \\
&(x_1^n) &(x_2^n) &\cdots &(x_4^n) &(y^n)
\end{pmatrix}
\Rightarrow
\begin{pmatrix}
&(x_0^0) &(x_1^0) &(x_2^0) &\cdots &(x_4^0) &(y^0)\\
&(x_0^1) &(x_1^1) &(x_2^1) &\cdots &(x_4^1) &(y^1)\\
& \cdots \\
&(x_0^n) &(x_1^n) &(x_2^n) &\cdots &(x_4^n) &(y^n)
\end{pmatrix}$$
有$$ \hat y^{(i)} = \theta _0 x_0^{(i)}+ \theta_1 x_1^{(i)}+ \theta_2 x_2^{(i)}+\cdots + \theta_n x_n^{(i)} $$
求解方法
-
代数法
-
矩阵法(向量法)
二者步骤一样:
1.确定损失函数,求其梯度表达式
损失函数:
$$J(\theta _0,\theta _1,\cdots , \theta _n) = \frac{1}{2m} \sum_{i=1}^{m}(y^{(i)} - \hat y^{(i)})^{2} = \frac{1}{2m} \sum_{i=1}^{m}(y^{(i)} - (\theta _0 x_0^{(i)}+ \theta_1 x_1^{(i)}+ \theta_2 x_2^{(i)}+\cdots + \theta_n x_n^{(i)} ))^2$$
系数$$ \frac{1}{2m} $$是为了方便求偏导
梯度表达式:
$$ \frac{\partial J(\theta _0,\theta _1,\cdots , \theta _n)}{\partial \theta _j} = \frac{1}{m}\sum_{i=1}^{m}(y^{(i)} - \hat y^{(i)})^{2}x_j^i $$
2.学习率乘以损失函数的梯度,得到当前位置下降的距离
$$\eta \frac{\partial J(\theta _0,\theta _1,\cdots , \theta _n)}{\partial \theta_j}$$
3.确定是否对于所有的 梯度下降的距离都小于 ,如果小于 则算法终止,当前所有的 即为所求。
4.更新 ,其更新表达式如下。更新完毕后继续转入步骤 1.
$$\theta _j^i = \theta _j^i - \eta \sum_{i=1}^{m}(y^{(i)} - \hat y^{(i)})^{2}x_j^i$$
三种梯度下降法(BGD、SGD、MBGD)
-
批量梯度下降法(Batch Gradient Descent)
-
批量梯度下降法,是梯度下降法最常用的形式,具体做法也就是在更新参数时使用所有的样本来进行更新
-
更新公式:
$$\theta _j^i = \theta _j^i - \eta \sum_{i=1}^{m}(y^{(i)} - \hat y^{(i)})^{2}x^i$$
-
-
随机梯度下降法(Stochastic Gradient Descent)
-
求梯度时没有用所有的 m 个样本的数据,而是仅仅选取一个样本 i 来求梯度
-
更新公式:
$$\theta _j^i = \theta _j^i - \eta (y^{(i)} - \hat y^{(i)})^{2}x^i$$
-
-
小批量梯度下降法(Mini-batch Gradient Descent)
-
小批量梯度下降法是批量梯度下降法和随机梯度下降法的折衷,也就是对于 m 个样本, 采用 x 个样本来迭代,1<x<m。一般可以取 x=10
-
更新公式:
-
$$\theta _j^i = \theta _j^i - \eta \sum_{i=1}^{m}(y^{(i)} - \hat y^{(i)})^{2}x^i$$