什么是梯度下降法？

564 人赞同了该回答

梯度下降法简单来说就是一种寻找目标函数最小化的方法。

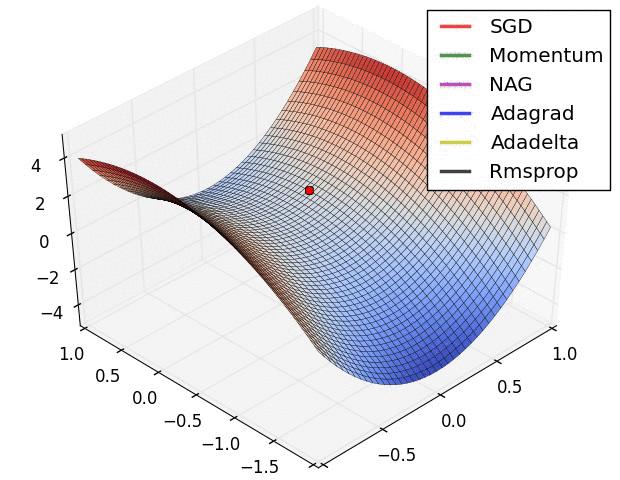
在深度学习中，经常有人会拿下面这幅图来比较各种优化算法的性质，包括传统的 SGD，Momentum SGD，AdaGrad，RMSProp 和 Adam 等。不过光看图可能无法理解其中的精妙之处，本文将会从数学的基础知识出发，初步介绍深度学习中的一些优化算法，最后进行一些简单的案例分析。

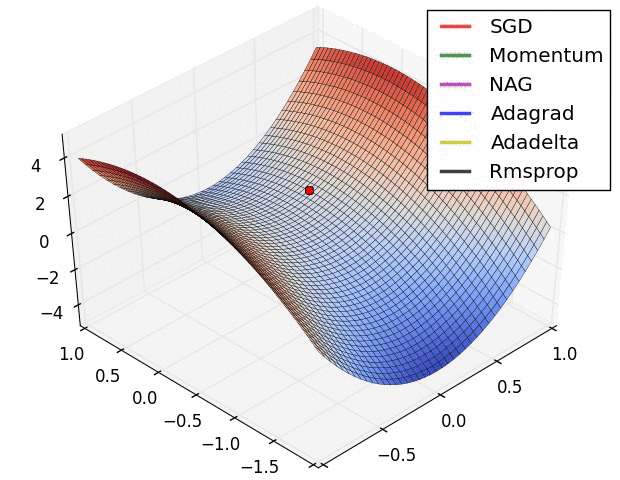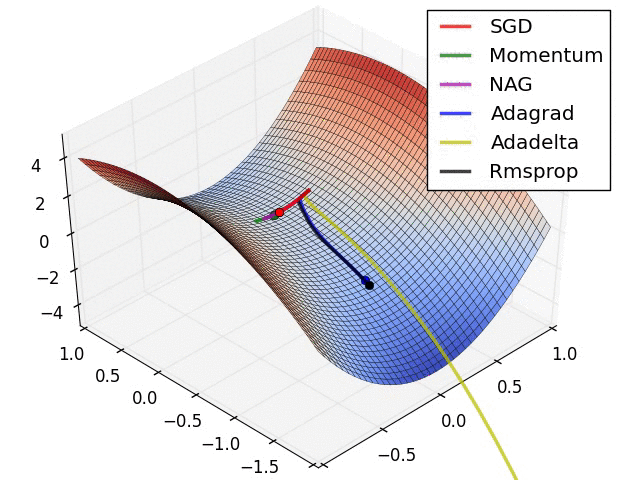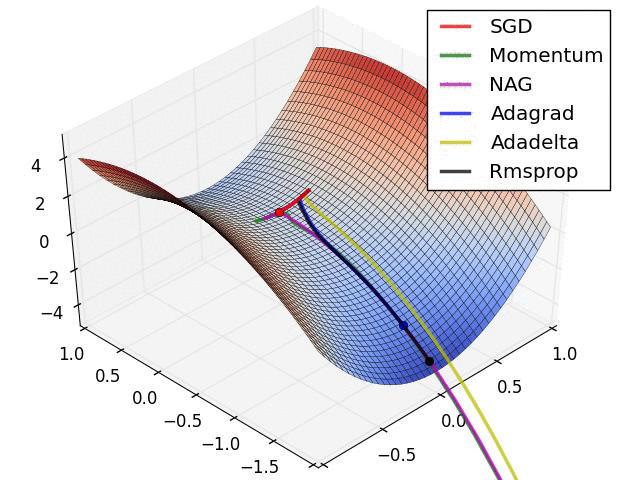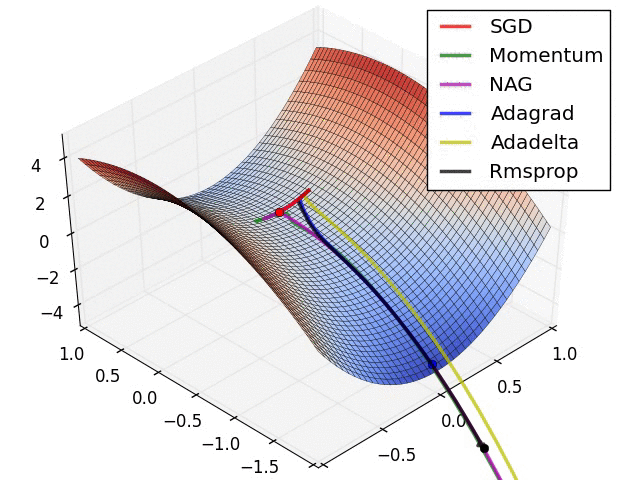
数学基础知识回顾

一元函数的导数与 Taylor 级数

在微积分中，函数 $f(x)$ 在点 $x_{0}$ 上的导数定义为： $f'(x_{0}) = \lim_{x\rightarrow x_{0}}\frac{f(x)-f(x_{0})}{x-x_{0}},$ 它在几何上指的就是函数 $f(x)$ 在 $x_{0}$ 上的切线方向。

通常来说，为了计算某个函数 $f(x)$ 的最大值或者最小值，通常都会计算它的导数 $f'(x)$ ，然后求解方程 $f'(x)=0$ 就可以得到函数的临界点，进一步判断这些临界点是否是最大值或者最小值。但是临界点并不一定是全局最大值或者全局最小值，甚至不是局部的最大值或者局部最小值。

例如：函数 $f(x) =x^3$ ，它的导数是 $f'(x)=3x^2$ ，因此 $x=0$ 是它的临界点。但 $x=0$ 则不是这个函数的局部最大值或者局部最小值点，因为 $f(x)<0, \forall x<0$ 且 $f(x)>0, \forall x>0$ 。

从 Taylor 级数的角度来看， $f(x)$ 在 $x_{0}$ 附近的 Taylor 级数是

$f(x) = f(x_{0}) + f'(x_{0})(x-x_{0}) + \frac{f''(x_{0})}{2}(x-x_{0})^{2} + O(|x-x_{0}|^{3}).$

对于临界点 $x_{0}$ 而言，它满足条件 $f'(x_{0}) = 0$ 。当 $f''(x_{0})>0$ 时，可以得到 $x_{0}$ 是 $f(x)$ 的局部最小值；当 $f''(x_{0})<0$ 时，可以得到 $x_{0}$ 是 $f(x)$ 的局部最大值。而对于上面的例子 $f(x)=x^3$ 而言，临界点 $0$ 的二阶导数则是 $f''(0)=0$ ，因此使用上面的方法则无法判断临界点 $0$ 是否是局部极值。

多元函数的梯度和 Taylor 级数

对于多元函数 $f(\bold{x}) = f(x_{1},\cdots, x_{n})$ 而言，同样可以计算它们的“导数”，也就是偏导数和梯度，i.e. 它的梯度可以定义为：

$\nabla f(\bold{x}) = \bigg(\frac{\partial f}{\partial x_{1}}(\bold{x}), \cdots, \frac{\partial f}{\partial x_{n}}(\bold{x})\bigg).$

而多元函数 $f(\bold{x})$ 在点 $\bold{x}_{0}$ 上的 Taylor 级数是：

$f(\bold{x}) = f(\bold{x}_{0}) + \nabla f(\bold{x}_{0})(\bold{x}-\bold{x}_{0}) + \frac{1}{2}(\bold{x}-\bold{x}_{0})^{T}H(\bold{x}-\bold{x}_{0}) + O(|\bold{x}-\bold{x}_{0}|^{3}),$

其中 $H$ 表示 Hessian 矩阵。如果 $x_{0}$ 是临界点，并且 Hessian 矩阵是正定矩阵的时候， $f(\bold{x})$ 在 $x_{0}$ 处达到局部极小值。

梯度下降法

从数学上的角度来看，梯度的方向是函数增长速度最快的方向，那么梯度的反方向就是函数减少最快的方向。那么，如果想计算一个函数的最小值，就可以使用梯度下降法的思想来做。假设希望求解目标函数 $f(\bold{x})=f(x_{1},\cdots,x_{n})$ 的最小值，可以从一个初始点 $\bold{x}^{(0)}=(x_{1}^{(0)},\cdots,x_{n}^{(0)})$ 开始，基于学习率 $\eta>0$ 构建一个迭代过程：当 $i\geq 0$ 时，

$\begin{eqnarray*} x_{1}^{(i+1)} &=& x_{1}^{(i)} - \eta\cdot \frac{\partial f}{\partial x_{1}}(\bold{x}^{(i)}), \\ &\cdots& \\ x_{n}^{(i+1)} &=& x_{n}^{(i)} - \eta\cdot \frac{\partial f}{\partial x_{n}}(\bold{x}^{(i)}). \end{eqnarray*}$

其中 $\bold{x}^{(i)} = (x_{1}^{(i)},\cdots,x_{n}^{(i)})$ ，一旦达到收敛条件的话，迭代就结束。从梯度下降法的迭代公式来看，下一个点的选择与当前点的位置和它的梯度相关。反之，如果要计算函数 $f(\bold{x})=f(x_{1},\cdots,x_{n})$ 的最大值，沿着梯度的反方向前进即可，也就是说：

$\begin{eqnarray*} x_{1}^{(i+1)} &=& x_{1}^{(i)} + \eta\cdot \frac{\partial f}{\partial x_{1}}(\bold{x}^{(i)}), \\ &\cdots& \\ x_{n}^{(i+1)} &=& x_{n}^{(i)} + \eta\cdot \frac{\partial f}{\partial x_{n}}(\bold{x}^{(i)}). \end{eqnarray*}$

其中 $\bold{x}^{(i)} = (x_{1}^{(i)},\cdots,x_{n}^{(i)})$ 。整体来看，无论是计算函数的最大值或者最小值，都需要构建一个迭代关系 $g$ ，那就是：

$\begin{eqnarray*} \bold{x}^{(0)} \stackrel{g}{\longrightarrow} \bold{x}^{(1)} \stackrel{g}{\longrightarrow} \bold{x}^{(2)} \stackrel{g}{\longrightarrow} \cdots, \end{eqnarray*}$

也就是说对于所有的 $i\geq 0$ ，都满足迭代关系 $x^{(i+1)}=g(x^{(i)})$ 。所以，在以上的两个方法中，我们可以写出函数 $g$ 的表达式为：

$\begin{eqnarray*} g(\bold{x})=\begin{cases} \bold{x} - \eta\nabla f(\bold{x}) &\text{梯度下降法},\\ \bold{x} + \eta\nabla f(\bold{x}) &\text{梯度上升法}. \end{cases} \end{eqnarray*}$

深度学习中的优化算法

在本文中，假设 $L$ 是每个样本的损失函数， $f(\bold{x};\Theta)$ 表示一个关于输入 $\bold{x}$ 和参数 $\Theta$ 的函数，并且 $\bold{y}$ 表示 $\bold{x}$ 所对应的目标值。

案例分析

案例1： $f(x,y) = (x^{2}+y^{2})/2$

针对这个函数 $f(x,y)=(x^2+y^2)/2$ 而言，从数学上我们可以轻易地得到最小值点就是 $(0,0)$ 。不过在这里我们可以验证随机梯度下降法的效果。首先计算函数 $f(x,y)$ 的梯度为：

$\begin{eqnarray*} \nabla f(x,y) = (x,y). \end{eqnarray*}$

其次，给定一个随机的初始点 $(x^{(0)},y^{(0)})$ ，通过梯度可以得到迭代公式为：

$\begin{eqnarray*} x^{(i+1)} &=& x^{(i)} - \eta \cdot \frac{\partial f}{\partial x}(x^{(i)},y^{(i)}) = (1 -\eta)\cdot x^{(i)},\\ y^{(i+1)} &=& y^{(i)} - \eta \cdot \frac{\partial f}{\partial y}(x^{(i)},y^{(i)}) = (1 - \eta)\cdot y^{(i)}. \end{eqnarray*}$

其中 $\eta\in(0,1)$ 表示学习率， $i\geq 0$ 表示迭代次数。因此，可以计算出具体的公式为：

$\begin{eqnarray*} x^{(i)} &=& (1-\eta)^{i}\cdot x^{(0)}, \\ y^{(i)} &=& (1-\eta)^{i}\cdot y^{(0)}. \end{eqnarray*}$

于是可以得到：

$\begin{eqnarray*} \lim_{i\rightarrow \infty} (x^{(i)}, y^{(i)}) = (0,0). \end{eqnarray*}$

意思就是说，使用随机梯度下降法我们可以得到函数 $f(x,y) = (x^2+y^2)/2$ 的最小值是 $(0,0)$ 。

案例2： $g(x,y) = (x^{2}-y^{2})/2$

不过，随机梯度下降法也有着自身的局限性。针对很多高维非凸函数而言，鞍点的数量其实远远大于局部极小值（极大值）的数量。因此，如何快速的逃离鞍点就是深度学习中大家所研究的问题之一。而比较简单的鞍点就是马鞍面函数 $g(x,y) = (x^2-y^2)/2$ 中的 $(0,0)$ 点。而函数 $g(x,y) = (x^{2}-y^{2})/2$ 在 $\mathbb{R}^{2}$ 上并没有最小值，因为 $\lim_{y\rightarrow\infty} g(x,y) = -\infty$ 。同时，函数 $g$ 的偏导数是：

$\begin{eqnarray*} \frac{\partial g}{\partial x} = x, \text{ } \frac{\partial g}{\partial y} = -y. \end{eqnarray*}$

而 $g(x,y)$ 在点 $(0,0)$ 上则满足以下几个性质：

$\begin{eqnarray*} \frac{\partial g}{\partial x}(0,0) &=& \frac{\partial g}{\partial y}(0,0)=0, \end{eqnarray*}$

$\begin{eqnarray*} H&=&\begin{pmatrix} \frac{\partial^{2}g}{\partial x^{2}}(0,0) & \frac{\partial^{2}g}{\partial x\partial y}(0,0) \\ \frac{\partial^{2}g}{\partial y\partial x}(0,0) & \frac{\partial^{2}g}{\partial y^{2}}(0,0) \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}. \end{eqnarray*}$

也就是说， $(0,0)$ 这一点的 Hessian 矩阵并不是正定矩阵。

随机梯度下降法：如果初始点是 $(x^{(0)},y^{(0)})$ ，那么随机梯度下降法（SGD）就可以写成：对于所有的 $i\geq 0$ ，有

$\begin{eqnarray*} x^{(i+1)} &=& x^{(i)} - \eta\cdot x^{(i)} = (1-\eta)\cdot x^{(i)}, \\ y^{(i+1)} &=& y^{(i)} + \eta\cdot y^{(i)} = (1+\eta)\cdot y^{(i)}. \end{eqnarray*}$

其中 $\eta\in(0,1)$ 是学习率。

使用动量的随机梯度下降法：如果初始点是 $(x^{(0)}, y^{(0)})$ ，初始速度是 $(v_{x}^{(0)}, v_{y}^{(0)})$ ，学习率是 $\eta\in(0,1)$ ，动量参数是 $\alpha\in (0,1)$ ，那么使用动量的随机梯度下降法就可以写成： $\forall i\geq 0$ ，

$\begin{eqnarray*} v_{x}^{(i+1)} &=& \alpha \cdot v_{x}^{(i)} - \eta\cdot x^{(i)}, \\ v_{y}^{(i+1)} &=& \alpha \cdot v_{y}^{(i)} + \eta\cdot y^{(i)},\\ x^{(i+1)} &=& x^{(i)} + v_{x}^{(i+1)} = (1-\eta)\cdot x^{(i)} + \alpha \cdot v_{x}^{(i)},\\ y^{(i+1)} &=& y^{(i)} + v_{y}^{(i+1)} = (1+\eta)\cdot y^{(i)} + \alpha \cdot v_{y}^{(i)}. \end{eqnarray*}$

AdaGrad 算法：如果初始点是 $(x^{(0)},y^{(0)})$ ，学习率是 $\eta \in(0,1)$ ， $\delta>0$ 是小常数，那么 AdaGrad 算法就可以写成： $\forall i\geq 1$ ，

$\begin{eqnarray*} x^{(i+1)} &=& x^{(i)} - \frac{\eta}{\delta + \sqrt{\sum_{k=0}^{i}\big(x^{(k)}\big)^{2}}} \cdot x^{(i)}, \\ y^{(i+1)} &=& y^{(i)} + \frac{\eta}{\delta + \sqrt{\sum_{k=0}^{i}\big(y^{(k)}\big)^{2}}} \cdot y^{(i)}, \end{eqnarray*}$

其中 $\eta \in (0,1)$ 是学习率， $\delta>0$ 是一个小常数。

Case 1： $y^{(0)} = 0$

当 $y^{(0)}=0$ 时，如果使用随机梯度下降法，就可以得到 $\forall i\geq 0$ ，

$\begin{eqnarray*} x^{(i)} &=& (1-\eta)^{i}\cdot x^{(0)}, \\ y^{(i)} &=& 0. \end{eqnarray*}$

因此， $\lim_{i\rightarrow 0} (x^{(i)}, y^{(i)})= (0,0)$ 。通过随机梯度下降法（SGD）在初始值为 $(x^{(0)},0)$ 的前提下并不能计算出函数 $g(x,y)$ 的最小值，而是会停止在 $(0,0)$ 鞍点这个地方，最终无法逃离鞍点。

同理，如果使用基于动量的 SGD 算法，就要看初始速度的设置了，如果初始的速度为 $(v_{x}^{(0)},v_{y}^{(0)}) = (0,0)$ ，那么最终都会收敛到 $(0,0)$ 这个点上。不过，如果 $v_{y}^{(0)}\neq 0$ ，那么就可以在一定次数的迭代之后逃离 $(0,0)$ 。

根据同样的分析思路，在本文中所写的 AdaGrad，RMSProp，Adam 算法中，如果初始点是 $(x^{(0)},0)$ 并且算法参数都是默认的话，使用这些方法同样无法逃离鞍点 $(0,0)$ ，也就是说最终都会收敛到 $(0,0)$ 上。

Case 2： $y^{(0)} \neq 0$

在这种情况下，可以考虑在 $(x_{0},0)$ 的基础上给纵坐标加上一个微小的扰动。不妨假设初始点为 $(1,10^{-11})$ 。下面计算各个算法在这个初始值下的收敛效果。在实际的应用中，需要迭代的次数越少越好。于是，通过计算 $\min\{i: y^{(i)}>1\}$ 的值，就可以进一步判断哪个算法（SGD，Momentum SGD，AdaGrad，RMSProp，Adam）更加容易逃离鞍点。

随机梯度下降法：通常情况下， $\eta$ 可以设置为 $0.01$ 。从随机梯度下降法的公式来看，就可以得到如下迭代公式：

$\begin{eqnarray*} x^{(i)} &=& (1-\eta)^{i}\cdot x^{(0)} = (1-0.01)^{i}, \\ y^{(i)} &=& (1+\eta)^{i}\cdot y^{(0)} = (1+0.01)^{i}\cdot 10^{-11}. \end{eqnarray*}$

其实， $\lim_{i\rightarrow \infty} (x^{(i)},y^{(i)}) = (0,\infty)$ ，i.e. 使用梯度下降法同样可以找到函数 $g(x,y) = (x^2-y^2)/2$ 的最小值。但是，如果 $y^{(i)} = (1+0.01)^{i}\cdot 10^{-11}>1$ ，则 $i$ 需要满足条件：

$\begin{eqnarray*} i \geq \frac{\ln(10^{11})}{\ln(1+0.01)} \approx 2546. \end{eqnarray*}$

换言之，需要迭代 $2546$ 次左右才能够使得 $y^{(i)}>1$ 。

AdaGrad 算法：通常来说，在 AdaGrad 算法中，算法的参数默认值是 $\eta = 10^{-2}$ 和 $\delta= 10^{-7}$ 。由于初始值 $y^{(0)} = 10^{-11}$ ，所以计算可以得到：

$\begin{eqnarray*} y^{(1)} &=& y^{(0)} + \frac{\eta}{\delta + |y^{(0)}|} \cdot y^{(0)} = 10^{-11} + \frac{10^{-2}}{10^{-7}+10^{-11}}\cdot 10^{-11} \approx 10^{-6},\\ y^{(2)} &=& y^{(1)} + \frac{\eta}{\delta + \sqrt{\sum_{k=0}^{1}\big(y^{(k)}\big)^{2}}} \cdot y^{(1)} \approx 10^{-6} + \frac{10^{-2}}{10^{-7}+10^{-6}}\cdot 10^{-6} \approx 10^{-2}.\\ \end{eqnarray*}$

最后通过写程序就可以证明，在 AdaGrad 的默认参数下，只需要 $1300$ 次左右的迭代就可以实现 $y^{(i)}>1$ 。

RMSProp 算法：

在这种情况下，为了简单起见，可以令衰减速率 $\rho=0$ ，那么同样可以写出迭代公式为： $\forall i\geq 1$ ，有

$\begin{eqnarray*} x^{(i+1)} = x^{(i)} - \frac{\eta}{\sqrt{\delta + (x^{(i)})^{2}}}\cdot x^{(i)},\\ y^{(i+1)} = y^{(i)} + \frac{\eta}{\sqrt{\delta + (y^{(i)})^{2}}}\cdot y^{(i)}. \end{eqnarray*}$

在 RMSProp 里面，一般来说小常数 $\delta = 10^{-6}$ ， $\eta = 10^{-2}$ 。通过直接计算可以知道，在这种情况和参数设置下，在迭代了 $60$ 轮左右的时候，就会出现 $y^{(i)}>1$ 的情况。

整体来说，在初始值为 $(1,10^{-11})$ 的情况下，无论是 SGD，Momentum SGD，AdaGrad 算法，还是 RMSProp 算法，都会逃离鞍点 $(0,0)$ 。只不过 AdaGrad 和 RMSProp 算法的逃离速度比 SGD 快了许多。

发布于 2019-02-24

赞同 564 22 条评论收藏喜欢收起

![在这里插入图片描述](https://img-blog.csdnimg.cn/20200221112404144.jpg)

kyle1314608

发布了258 篇原创文章 · 获赞 7 · 访问量 2万+

私信关注