机器模型简介（一）：线性回归

在回归问题中，我们通过构建一个关于x的模型来预测y。这种问题通常可以利用线性回归(Linear Regression)来解决。

模型的目标值y是输入变量x的线性组合。表达形式为：

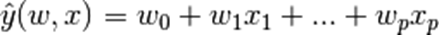
其中hat{y} 是预测值，向量w = (w_0，...，w_p)为模型参数，w_0为截距项，w_1...w_p为成员系数。以下是求解回归模型的一系列方法。

一、最小二乘法

最小二乘法是求解使得数据集实际观测数据和预测数据（估计值）之间残差平方和最小时的模型参数。数学形式可表达为：

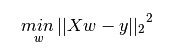
以下是用python3实现最小二乘回归的小例子。求解可得w0 = 0，w1 = 0.5，w2 = 0.5。

from sklearn import linear_model
clf = linear_model.LinearRegression()
clf.fit([[0, 0], [1, 1], [2, 2]], [0, 1, 2])
print('w0:', clf.intercept_) 
print('wi:', clf.coef_)

最小二乘回归

最小二乘法虽然求解简单，然而其系数估计依赖模型各项相互独立。当各项是相关的，设计矩阵(Design Matrix) 的各列近似线性相关，那么，设计矩阵会趋向于奇异矩阵，这会导致最小二乘估计对于随机误差非常敏感，会产生很大的方差。这种多重共线性(multicollinearity) 的情况可能真的会出现，比如未经实验设计收集的数据。

二、Lasso

Lasso通过对回归系数增加L1罚项来解决普通最小二乘法的一些问题。回归系数通过最小化带L1罚项的残差平方和求得。其目标函数是最小化：

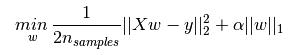
lasso解决带罚项的最小平方和，其中是一个常量，为是参数向量的L1范数。

以下是用python3实现Lasso的小例子。令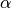 = 0.1，求解可得w0 = 0.15，w1 = 0.85，w2 = 0。

from sklearn import linear_model
clf = linear_model.Lasso(alpha = 0.1)
clf.fit([[0, 0], [1, 1], [2, 2]], [0, 1, 2])
print('w0:', clf.intercept_) 
print('wi:', clf.coef_)

Lasso

Lasso是一种估计稀疏线性模型的方法。它倾向具有少量参数值的情况，能有效的减少变量数量。因此，Lasso及其变种是压缩感知(压缩采样)的基础。在约束条件下，它可以回复一组非零精确的权重系数。

三、岭回归

岭回归（Ridge）通过对回归系数增加L2罚项来解决普通最小二乘法的一些问题。回归系数通过最小化带L2罚项的残差平方和求得，数学形式可表达为：

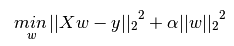
上述公式中，是控制模型复杂度的因子(可看做收缩率的大小，值大于0)。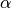越大，收缩率越大，那么系数对于共线性的鲁棒性更强。

以下是用python3实现岭回归的小例子。令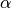 = 0.5，求解可得w0 = 011，w1 = 0.44，w2 = 0.44。

from sklearn import linear_model
clf = linear_model.Ridge (alpha = 0.5)
clf.fit([[0, 0], [1, 1], [2, 2]], [0, 1, 2])
print('w0:', clf.intercept_) 
print('wi:', clf.coef_)

岭回归

四、贝叶斯回归

线性模型假设我们的目标值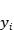服从高斯分布，接下去可以极大似然法来估计参数，一旦得到参数，整个学习就结束了。贝叶斯线性回归（Bayesian Linear Regression）也是估计参数，但是应用了贝叶斯定理，我们不仅要考虑似然，还要考虑先验以及证据因子：

其中参数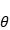只是一个向量，用来表示分布的参数。最重要的地方在于，所谓的后验概率是结果出现之后对概率的修正，从贝叶斯的视角看待整个数据集，我们会把样本的每个点进行增量计算，对于初始点，我们假设先验和似然，计算出它的后验，然后将初始点的后验估计当作下一次（两个样本点）估计的先验，如此反复，直到计算完毕整个数据集。可以想象到，随着样本的增加，我们的估计会越来越准确。

出于解析的目的，我们选取自共轭先验，我们假设似然函数服从高斯分布，先验分布服从高斯分布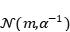。由于高斯分布的自共轭的性质，我们的后验分布也会是一个高斯分布，我们可以通过贝叶斯定理将后验高斯分布的参数用其余参数来表示：

后验分布的均值由两部分组成，一部分是先验的参数，另一部分是似然的参数，先验的精度越高（标准差越小），其对后验均值的影响就越大（体现为权重越大）。贝叶斯回归的过程是一个样本点逐步增加到学习器的过程，前一个样本点的后验会被下一次估计当作先验。岭回归实际上是加了均值为零的高斯先验。在这里，我们同样可以令先验的均值m=0，然后利用最大后验估计，忽略常数项得到：

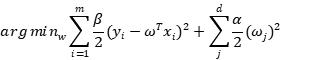
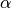这样的回归方式叫做贝叶斯岭回归（Bayesian Ridge regression）。它与普通岭回归的区别在于，它采用了贝叶斯逐步更新先验的策略，普通的岭回归允许参数

为零，因为这样就退化到了最小二乘回归，但贝叶斯估计不能这样做，因为高斯分布的标准差不能无穷大。

以下是用python3实现贝叶斯岭回归的小例子。求解可得w0 = 5.02，w1 = 0.5，w2 = 0.5。

from sklearn import linear_model
clf = linear_model.BayesianRidge()
clf.fit([[0, 0], [1, 1], [2, 2]], [0, 1, 2])
print('w0:', clf.intercept_) 
print('wi:', clf.coef_)
print(clf.predict([[3, 3]]))

贝叶斯岭回归

大多数情况下，计算贝叶斯的后验概率是一件非常困难的事情，我们选取共轭先验使得计算变得非常简单，其他的常见的方法有Laplace approximation，Monte Carlo积分（我们几乎都要用Markov Chain的平稳分布去逼近后验分布）。

机器模型简介（一）：线性回归

猜你喜欢