Dijkstra算法采用的是一种贪心的策略
。
声明一个数组dis来保存源点到各个顶点的最短距离,
再声明一个数组保存已经找到了最短路径的顶点的集合:T,
。
初始时,原点 s 的路径权重被赋为 0 (dis[s] = 0)。
若对于顶点 s 存在能直接到达的边(s,m),则把dis[m]设为w(s, m),同时把所有其他(s不能直接到达的)顶点的路径长度设为无穷大。
初始时,集合T只有顶点s
。
然后,从dis数组选择最小值,则该值就是源点s到该值对应的顶点的最短路径,并且把该点加入到T中,此时完成一个顶点,
然后,我们需要看看新加入的顶点是否可以到达其他顶点并且看看通过该顶点到达其他点的路径长度是否比源点直接到达短,
如果是,那么就替换这些顶点在dis中的值。
然后,又从dis中找出最小值,重复上述动作,直到T中包含了图的所有顶点。
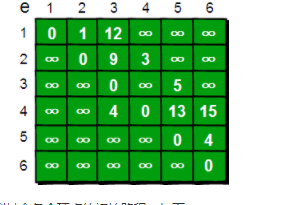
与Floyd-Warshall算法一样这里仍然使用二维数组e来存储顶点之间边的关系
我们还需要用一个一维数组dis来存储1号源点(假设源点为1号)到其余各个顶点的初始路程,如下。

Step 1:
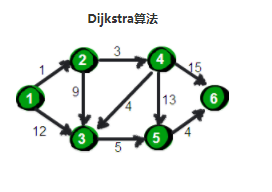
既然是求1号顶点到其余各个顶点的最短路程,那就先找一个离1号顶点最近的顶点。
通过数组dis可知当前离1号顶点最近是2号顶点。
当选择了2号顶点后,dis[2]的值就已经从“估计值”变为了“确定值”,即1号顶点到2号顶点的最短路程就是当前dis[2]值。
为什么呢?你想啊,目前离1号顶点最近的是2号顶点,并且这个图所有的边都是正数,
那么肯定不可能通过第三个顶点中转,使得1号顶点到2号顶点的路程进一步缩短了。
因为1号顶点到其它顶点的路程肯定没有1号到2号顶点短
。
。
Step 2:
既然选了2号顶点,接下来再来看2号顶点有哪些出边呢。
有2->3和2->4这两条边。先讨论通过2->3这条边能否让1号顶点到3号顶点的路程变短。
也就是说现在来比较dis[3]和dis[2]+e[2][3]的大小。
其中dis[3]表示1号顶点到3号顶点的路程。
dis[2]+e[2][3]中dis[2]表示1号顶点到2号顶点的路程,e[2][3]表示2->3这条边。
所以dis[2]+e[2][3]就表示从1号顶点先到2号顶点,再通过2->3这条边,到达3号顶点的路程。
。
。
Step 3:
我们发现dis[3]=12,dis[2]+e[2][3]=1+9=10,dis[3]>dis[2]+e[2][3],
因此dis[3]要更新为10。
这个过程有个专业术语叫做“松弛”。
即1号顶点到3号顶点的路程即dis[3],通过2->3这条边松弛成功。
这便是Dijkstra算法的主要思想:通过“边”来松弛1号顶点到其余各个顶点的路程。
同理通过2->4(e[2][4]),可以将dis[4]的值从∞松弛为4
(dis[4]初始为∞,dis[2]+e[2][4]=1+3=4,dis[4]>dis[2]+e[2][4],因此dis[4]要更新为4)。
。
。
Step 4:
刚才我们对2号顶点所有的出边进行了松弛。松弛完毕之后dis数组为:

接下来,继续在 剩下的3、4、5和6号顶点中 ,选出离1号顶点最近的顶点。
通过上面更新过dis数组,当前离1号顶点最近是4号顶点。
此时,dis[4]的值已经从“估计值”变为了“确定值”。
下面继续对4号顶点的所有出边(4->3,4->5和4->6)
用刚才的方法进行松弛。松弛完毕之后dis数组为:
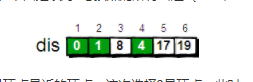
继续在 剩下的3、5和6号顶点中 ,选出离1号顶点最近的顶点,这次选择3号顶点。此时,dis[3]的值已经从“估计值”变为了“确定值”。对3号顶点的所有出边(3->5)进行松弛。松弛完毕之后dis数组为:
。
。
。
。
。
总结一下刚才的算法。
算法的基本思想是:
每次找到离源点(上面例子的源点就是1号顶点)最近的一个顶点,
然后以该顶点为中心进行扩展,最终得到源点到其余所有点的最短路径。
基本步骤如下:
将所有的顶点分为两部分:已知最短路程的顶点集合P和未知最短路径的顶点集合Q。
最开始,已知最短路径的顶点集合P中只有源点一个顶点。
我们这里用一个book[ i ]数组来记录哪些点在集合P中。
例如对于某个顶点i,如果book[ i ]为1则表示这个顶点在集合P中,如果book[ i ]为0则表示这个顶点在集合Q中。
设置源点s到自己的最短路径为0即dis=0。
若存在源点有能直接到达的顶点i,则把dis[ i ]设为e[s][ i ]。
同时把所有其它(源点不能直接到达的)顶点的最短路径为设为∞。
在集合Q的所有顶点中选择一个离源点s最近的顶点u(即dis[u]最小)加入到集合P。
并考察所有以点u为起点的边,对每一条边进行松弛操作。
例如存在一条从u到v的边,那么可以通过将边u->v添加到尾部来拓展一条从s到v的路径,这条路径的长度是dis[u]+e[u][v]。
如果这个值比目前已知的dis[v]的值要小,我们可以用新值来替代当前dis[v]中的值。
重复第3步,如果集合Q为空,算法结束。最终dis数组中的值就是源点到所有顶点的最短路径。
代码:
#include <stdio.h>
int main()
{
int e[10][10],dis[10],book[10],i,j,n,m,t1,t2,t3,u,v,min;
int inf=99999999;
//用inf(infinity的缩写)存储一个我们认为的正无穷值
//读入n和m,n表示顶点个数,m表示边的条数
scanf("%d %d",&n,&m);
//初始化
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if(i==j)
e[i][j]=0;
else
e[i][j]=inf;
//读入边
for(i=1;i<=m;i++)
{
scanf("%d %d %d",&t1,&t2,&t3);
e[t1][t2]=t3;
}
//初始化dis数组,这里例题是1号顶点到其余各个顶点的初始路程
for(i=1;i<=n;i++)
dis[i]=e[1][i];
//book数组初始化
for(i=1;i<=n;i++)
book[i]=0;
book[1]=1; //例题
//Dijkstra算法核心语句
for(i=1;i<=n-1;i++) //要遍历到除源点以外的每一个点
{
//找到离1号顶点最近的顶点
min=inf;
for(j=1;j<=n;j++)
{
if(book[j]==0 && dis[j]<min) //没找过这个点并且 小
{
min=dis[j];
u=j;
}
}
book[u]=1; //标记
for(v=1;v<=n;v++)
{
if(e[u][v]<inf) //剪枝
{
if(dis[v]>dis[u]+e[u][v])
dis[v]=dis[u]+e[u][v];
}
}
}
//输出最终的结果
for(i=1;i<=n;i++)
printf("%d ",dis[i]);
getchar();
getchar();
return 0;
}
毛学姐模板:
#include <bits/stdc++.h>
using namespace std;
const int INF = 0x3f3f3f3f;
const int N = 205;
int arr[N][N];
int dis[N];
bool vis[N];
int n, m, st, ed;
inline void init()
{
for(int i = 0; i < n; ++i)
for(int j = 0; j < n; ++j)
arr[i][j] = (i == j ? 0 : INF);
}
void Dijkstra()
{
int k = 0;
for(int i = 0; i < n - 1; ++i) {//次数
int minv = INF;
for(int j = 0; j < n; ++j)
if(dis[j] < minv && !vis[j]) minv = dis[j], k = j;
vis[k] = true;
for(int v = 0; v < n; ++v) {
if(arr[k][v] < INF) {
dis[v] = min(dis[v], dis[k] + arr[k][v]);
}
}
}
}
int main()
{
int a, b, c;
while(cin >> n >> m) {
init();
for(int i = 0; i < m; ++i) {
cin >> a >> b >> c;
if(arr[a][b] > c)
arr[a][b] = arr[b][a] = c;
}
cin >> st >> ed;
//初始化距离数组
for(int i = 0; i < n; ++i) dis[i] = arr[st][i];
//初始化vis数组
memset(vis, false, sizeof vis);
vis[st] = true;
Dijkstra();
cout << (dis[ed] == INF ? - 1 : dis[ed]) << endl;
}
return 0;
}
参考:
http://ahalei.blog.51cto.com/4767671/1387799
https://blog.csdn.net/qq_39521554/article/details/79333690