单源最短路径问题,即在图中求出给定顶点到其它任一顶点的最短路径。在弄清楚如何求算单源最短路径问题之前,必须弄清楚最短路径的最优子结构性质。
一.最短路径的最优子结构性质
该性质描述为:
如果P(i,j)={Vi…Vk…Vs…Vj}是从顶点i到j的最短路径,k和s是这条路径上的一个中间顶点,那么P(k,s)必定是从k到s的最短路径。
下面证明该性质的正确性:
假设P(i,j)={Vi…Vk…Vs…Vj}是从顶点i到j的最短路径,则有P(i,j)=P(i,k)+P(k,s)+P(s,j)。而P(k,s)不是从k到s的最短距离,那么必定存在另一条从k到s的最短路径P’(k,s),那么P’(i,j)=P(i,k)+P’(k,s)+P(s,j)<P(i,j)。则与P(i,j)是从i到j的最短路径相矛盾。因此该性质得证。
二、算法描述
2.1 算法思想
-
设G=(V,E)是一个带权有向图,把图中顶点集合V分成两组,第一组为已求出最短路径的顶点集合(用S表示,初始时S中只有一个源点,以后每求得一条最短路径 , 就将加入到集合S中,直到全部顶点都加入到S中,算法就结束了),第二组为其余未确定最短路径的顶点集合(用U表示),按最短路径长度的递增次序依次把第二组的顶点加入S中。
-
在加入的过程中,总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。
-
此外,每个顶点上标记一个距离,该距离就是当前步骤下,从v到此顶点的最短路径长度。
2.2 算法步骤
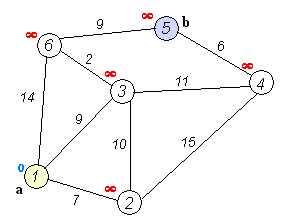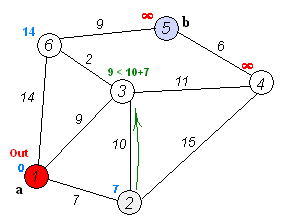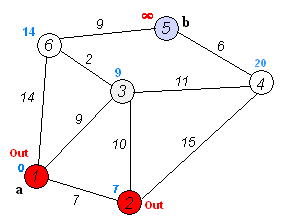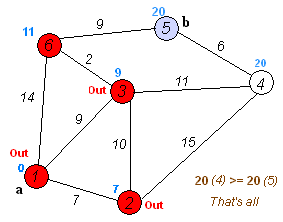
a.初始时,S只包含源点,即S={v},v到源点的距离为0。U包含除v外的其他顶点,即:U={其余顶点},若v与U中顶点u为邻接结点,则<u,v>有权值,若u不是v的邻接结点,则<u,v>权值为∞。
b.从U中选取一个距离源点v最小的顶点k,把k加入S中(该选定的距离就是v到k的最短路径长度)。
c.以k为新考虑的中间点,修改U中各顶点的距离:若从源点v 经过顶点k 到顶点u的距离 比 原来标记的距离短,则修改顶点u的距离值为顶点k上标记的距离加上<k,v>的权。
d.重复步骤b和c直到所有顶点都包含在S中。
执行动画过程如下图: