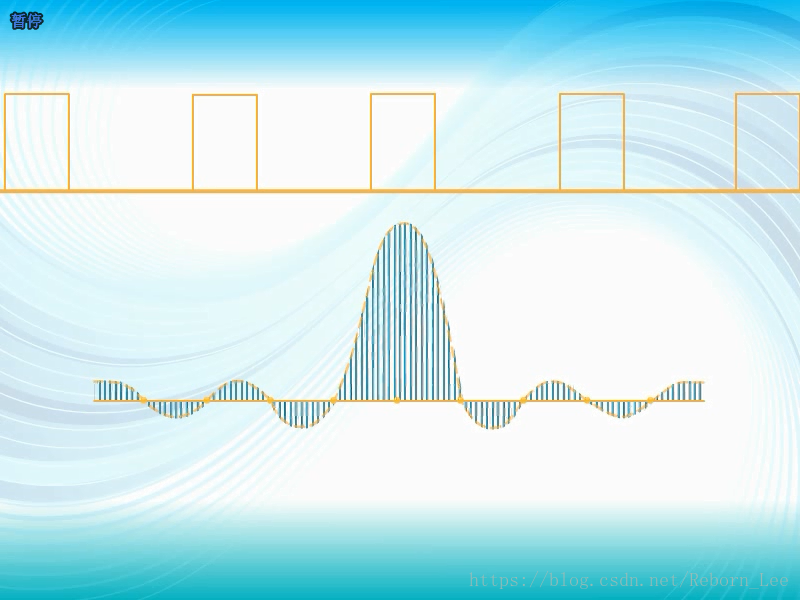
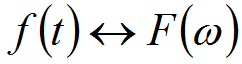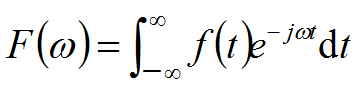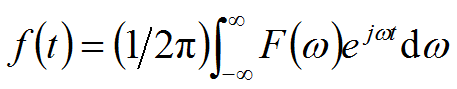基本概念
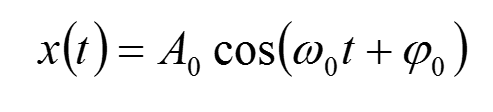
欧拉公式
根据欧拉公式正余弦信号还可以被指数形式所表示
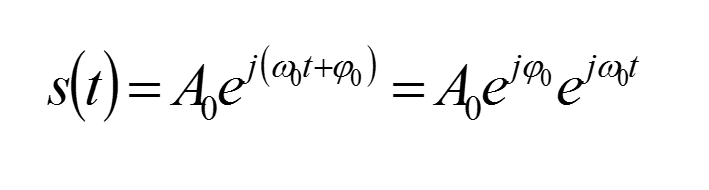
角频率或频率为横轴，振幅和相位为纵轴，画一个坐标系，表示这个正弦信号
在新的坐标系（角频率或频率为横轴，，振幅和相位为纵轴）中，以两条线（甚至两个点就够了），表示了时域波形如图2.1所示的信号，或者说，表示了信号所有的特征信息（频率、幅度和相位）。这种表示法被称为频域表示，表示的结果叫做“频谱”，对应于振幅或者相位分别为幅度谱和相位谱。
上述正弦信号只有单一频率，因此其频谱只包含一根“线”（谱线），人们常称其为“单色”信号。
傅里叶级数
公式推导，百度或者数学课本。
任何周期信号都能够由不同谐波的正弦波叠加而成，这由傅里叶发现，因此称之为傅里叶级数
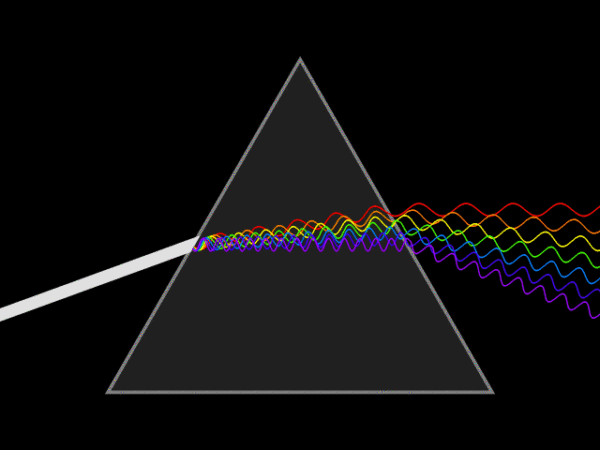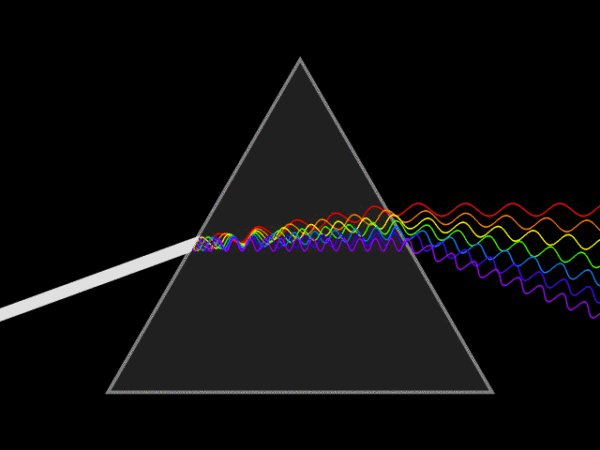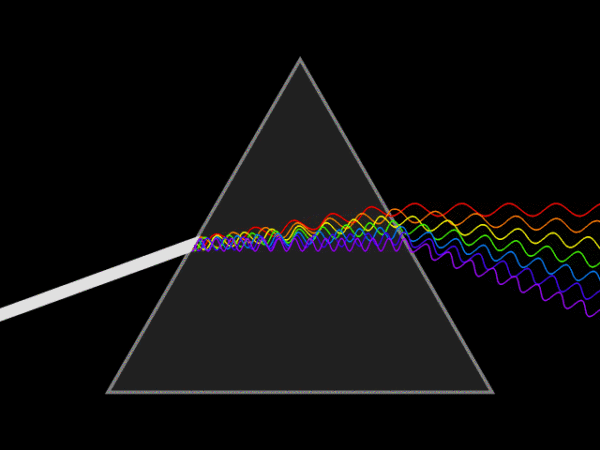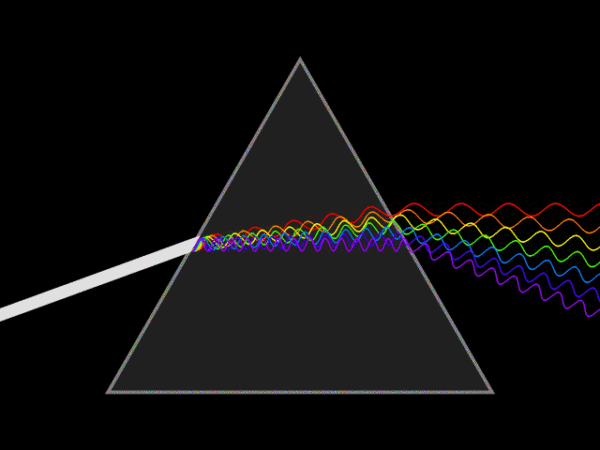
可以通过积化和差，把sin和cos化为一个cos
如果我把一个信号的所有正弦分量的频率算出来画出来，那么就如下图 ，也叫频谱图
频谱是频率谱密度的简称，是频率的分布曲线。复杂振荡分解为振幅不同和频率不同的谐振荡，这些谐振荡的幅值按频率排列的图形叫做频谱
考察某个信号的所有正弦分量，这些正弦分量覆盖的频率范围，被形象地叫做“频带”。这个范围的大小，就是“带宽”——即频带宽度，如图所示。带宽是衡量信号特性的一个重要指标。
极端情况下，相邻谱线足够接近时，频谱就可表示成连续的曲线了，原来分立的谱线于是简化为曲线中的一个个点 。
根据欧拉公式也可以用指数来表示一个周期信号
欧拉公式
因此傅里叶级数还可以表示成以下指数形式
如果我把一个信号的所有指数分量的频率算出来画出来，那么就如下图
可以看到，复频谱除正频率分量外，还包括负频率分量。负频率的出现是数学运算（欧拉公式）的结果，并无物理意义。
总结：
上述正弦信号只有单一频率，因此其频谱只包含一根“线”（谱线），人们常称其为“单色”信号。而在大多数应用场合中，信号是由若干不同频率的单色信号叠加而成的，称为“复合”信号。从频域角度看，复合信号的频谱包含若干条甚至无数条谱线。
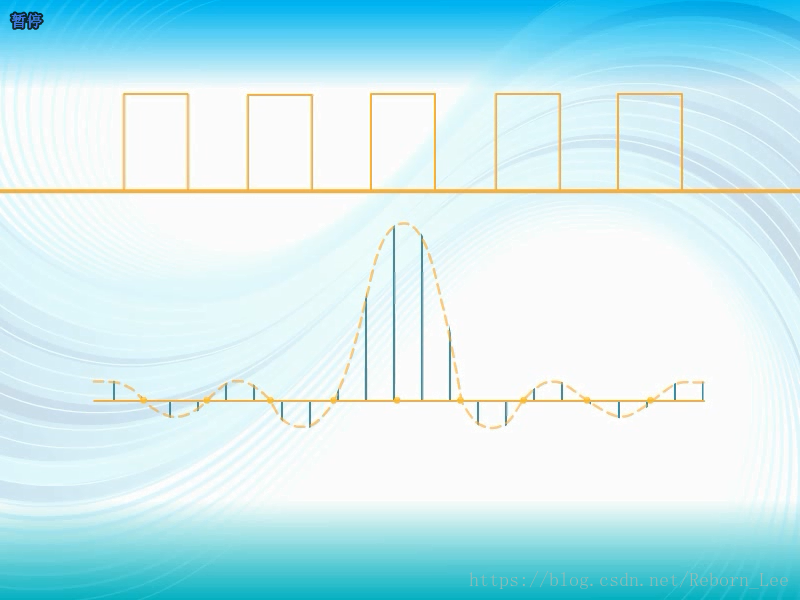
以周期矩形信号为例，从傅里叶级数到傅里叶变换
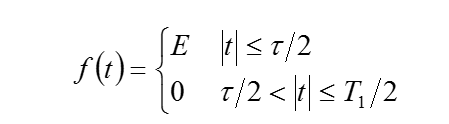
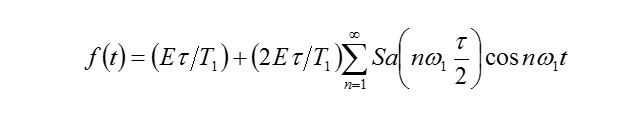
突然发现好多数学式子啊，知道它是很多正弦信号组成的，那我们来大概看看，小的正弦信号怎么组成了这个周期矩形信号
看到了吧，如果我再加更多的频率更高的正弦信号那么越像周期矩形信号。
有没有发现前面的正弦信号，矩形脉冲信号，都是周期信号。那么非周期信号怎么办呢？
傅里叶认为，既然周期信号可以用正弦信号来表示，那么非周期信号也可以用正弦信号来逼近。原因是非周期信号可以看成是周期无限大
的周期信号；事实证明，傅里叶的想法是对的，于是才有了大名鼎鼎的傅里叶变换。
再回顾一下傅里叶级数的三角函数形式
由于谱间隔为
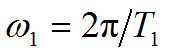
另外谱的幅度
所以当周期
无限增大时，谱线间隔会变密，而谱的幅度会减小。
极端情况下，若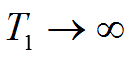
，周期函数转换为非周期函数，这时离散频谱将成为连续频谱，分量幅值趋于无穷小。
由于
增大时，带宽
减小
减小时，带宽增大
这反映了一个普遍的规律：时域上压缩，减小，频域上展宽，增大
考虑一个极端情况，若 
，即矩形脉冲变成冲击函数
，则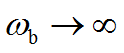
，频谱的高阶谐波分量不衰减，成为所谓的白色谱
