假定要求1-maxn范围内的所有素数并保存在数组中,下面是4种方法的分析。
这些方法也可通过预处理来判断素数
这些方法的时间复杂度从上到下越来越低。
方法一:逐个判断(普通)
bool isPrime(int num )
{
for(int i= 2; i*i <= num ; i++)
if(num %i== 0)
return 0 ;
return 1 ;
}
//若一个数可以进行因数分解,得到的两个数一定是一个小于等于sqrt(n),一个大于等于sqrt(n)。
//据此,上述代码中并不需要遍历到n-1,遍历到sqrt(n)即可。
//因为若sqrt(n)左侧找不到约数,那么右侧也一定找不到约数。
int main(){
int prime[1000],count=0;//prime数组中能存放1000个素数
for(int i=2;i<=maxn;i++)//判断范围为[2,maxn]
if(isPrime(i)) prime[count++]=i;
return 0;
}至此方法一能得到<=maxn的所有素数,时间复杂度O(n√n)
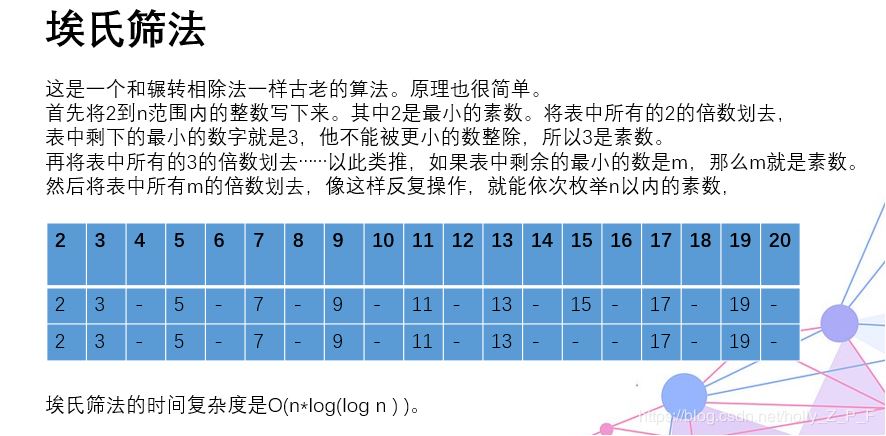
方法二:埃氏筛法
int main()
{
static bool isPrime[maxn];//利用static特性将数组值全部置为0 即false
isPrime[0]=isPrime[1]=ture;//1 0 不是素数标记为ture
for(int i=2;i<=maxn;i++)//从2开始往后筛 直至maxn
{
if(!isprime[i])//如果是素数,则用它来筛出它的倍数(它的倍数一定不是素数)
for(int j=2*i;j<=maxn;j+=i)//起始值2*j,随后变成3*j 4*j,直至大于maxn结束
isprime[j]=ture; //将其倍数标记为ture 不是素数
}
}尽管时间复杂度比上面优秀 但还是能发现存在不足: 有数被重复筛选了。如 12=2*6=3*4=4*3
方法三:埃氏筛法改进
我们可以将循环初始值直接设置为int j=i*i,减少筛选次数。原因如下:
首先补充一个数论知识:任何一个大于1的自然数 ,如果N不为素数,都可以唯一分解成有限个素数的乘积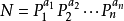
为什么不需要遍历(2~i-1)*i部分呢? 因为他们肯定已经被遍历过了 。
对于2~i-1中的素数in,它肯定是小于i的,在i进入循环前就已经通过2*in , 3*in , 4*in , ......i*in 的形式标记过了 in*i ,所以不需要标记。
对于2~i-1中的非素数ik,既然是非素数,可以拆分成素数之积 如20=2*2*5,假设此时ik=20,那么ik*i是不是可以写成 2*(2*5*i)的形式呢,拆分出来的素数肯定小于i,那么它已经通过2*2, 3*2, 4*2,...,(2*5*i)*2的形式被标记了。
至此我们证明了可以直接设置循环初始条件为int j=i*i
时间复杂度相比改进前而言降低了
代码与上面比较只改变了一处
int main()
{
static bool isPrime[maxn];
isPrime[0]=isPrime[1]=ture;
for(int i=2;i<=maxn;i++)
{
if(!isprime[i])
for(int j=i*i;j<=maxn;j+=i)//改变处
isprime[j]=ture;
}
}如102=2*51=3*34=17*6(前一个乘积是素数) ,对于17*6来说,如果将其初始设置为2*17,那么它不可避免会重复筛到102即6*17。改进后初始值设置为17*17,那它不会筛到102,减少了无效筛选次数。当然这只是一点点改进,比如对于3*34来说,就算设置为3*3,它也会筛选到102.还有一种更好的筛法可以来保证每个合数只被筛选一次,那就是下面的欧拉筛法。
方法四:欧拉筛法(线性筛)
基本思想:任何合数都能表示成多个素数的积。所以,任何的合数肯定有一个最小质因子。我们通过这个最小质因子就可以判断什么时候不用继续筛下去了。
代码很短,关键点理解方式我以注释的形式写出来了。
#include<stdio.h>
#include<string.h>
using namespace std;
int main()
{
int maxn,cnt=0;
static int prime[1000];//能存1000个素数 static特性能将其全部初始化为0
scanf("%d", &maxn);
static bool vis[maxn];//每个数都初始化标签为0 即false
for(int i = 2; i <= maxn; i++)
{
if(!vis[i])//不是目前找到的素数的倍数 (即为素数)
prime[cnt++] = i;//找到素数 按顺序存入prime数组
for(int j = 0; j<cnt && i*prime[j]<=n; j++) //从小到大取出数组中的素数
{ //进入这个for循环的i都是合数哦
vis[i*prime[j]] = true;//找到的素数的倍数标记,最初j=0,prime[j]是第一个素数2
if(i % prime[j] == 0) break;//关键!!!!
//首先我们规定每个合数只能被含有它最小素数因子的等式表达,即i*prime[]_min
//例子 6=2*3 9=3*3 20=2*10 它们的最小素数因子是2,3 ,2
//对于6 9 20这三个数,只有i=3,3,10时能被标记,i*合数的最小素数因子=合数
//这样就保证只被合法的i进入循环时标记一次这个合数
//素数因子是放在prime里面的,从小到大取出
//从素数2开始,2乘i肯定是这个合数的含最小素数因子的等式表达,因为最小素数就是2
//那么接下来判断i%prime[j]==0
//i%prime[j]==0表示素数prime[j]是i的因子
//如果是,为什么要break呢?
//因为如果是,就表示这个i能拆成 prime[j]*N(N为整数) 的形式
//那么对于prime[j+1],也就是下一个素数,i * prime[j]就不是那个含最小素数因子的表达式了,
//i*primer[j]=prime[j]*N*prime[j+1] ,这里面还有个小于prime[j+1]素数因子prime[j]可以分出来。
//由规定,这个i就不合法了,你继续往后prime[j+n]也没用了,总是能分出一个小于它们的prime[j]
//所以直接break,让下一个i进入。
//不用担心后面的合数不会被标记到
//这个公式i*primer[j]=prime[j]*N*prime[j+1] 合法的i=N*prime[j+1]
//而当前break的i=N*prime[j] 因为prime[j+1]>prime[j]
//我们要找的i在后面。
//这是我对于这一行的理解方式
}
}
return 0;
}