质数又称素数,指在一个大于1的自然数中,除了1和此整数自身外,没法被其他自然数整除的数。换句话说,只有两个正因数(1和自己)的自然数即为素数。比1大但不是素数的数称为合数。1和0既非素数也非合数。合数是由若干个质数相乘而得到的。
质数的判断:
1、只能被1和本身整除。
2、不能被小于它的平方根的所有素数整除就是素数。
一、常规算法
直接用定义做,判断n是否为素数,就用2~n-1去除n,如能被整除则不是素数,否则为素数。代码如下:
求n以内的所有素数的时间复杂度:O(n²)
def isprime(n):
for j in range(2, n): # 2~n-1,不包括n
if (n % j == 0): # 能被2~n-1(不包括n)整除,不是素数
return False
else:
return True # 循环正常结束是素数(没有被整除)
P = []
for i in range(2, 10**8+1): # 求10⁸以内的素数
if isprime(i):
P.append(i)
print(P)二、常规优化算法
上述算法中循环次数为2~n-1,共n-2次。因为因数是成对出现的,一个小于等于算术平方根,另外一个大于等于算术平方根。所以只需测试小于等于算术平方根的因数是否存在,如存在则不是素数,否则就是素数。代码如下:
求n以内的所有素数的时间复杂度:,即
def isprime(n):
j = 2
while j * j <= n: # j为2~n**0.5
if (n % j == 0): # 能被2~n-1(不包括n)整除,不是素数
return False
j += 1
else:
return True # 循环正常结束是素数(没有被整除)
P = []
for i in range(2, 10**8+1): # 求10⁸以内的素数
if isprime(i):
P.append(i)
print(P)三、用埃氏筛法优化
什么是埃氏筛?埃拉托斯特尼筛法(Eratosthene sieve method),简称埃氏筛或爱氏筛,是一种由希腊数学家埃拉托斯特尼所提出的一种简单检定素数的算法。 要得到自然数n以内的全部素数,必须把不大于根号n的所有素数的倍数剔除,剩下的就是素数。 要得到自然数n以内的全部素数,必须把不大于 的所有素数的倍数剔除,剩下的就是素数。
简而言之:就是把素数的倍数的数全部剔除掉,剩下的数就是素数。
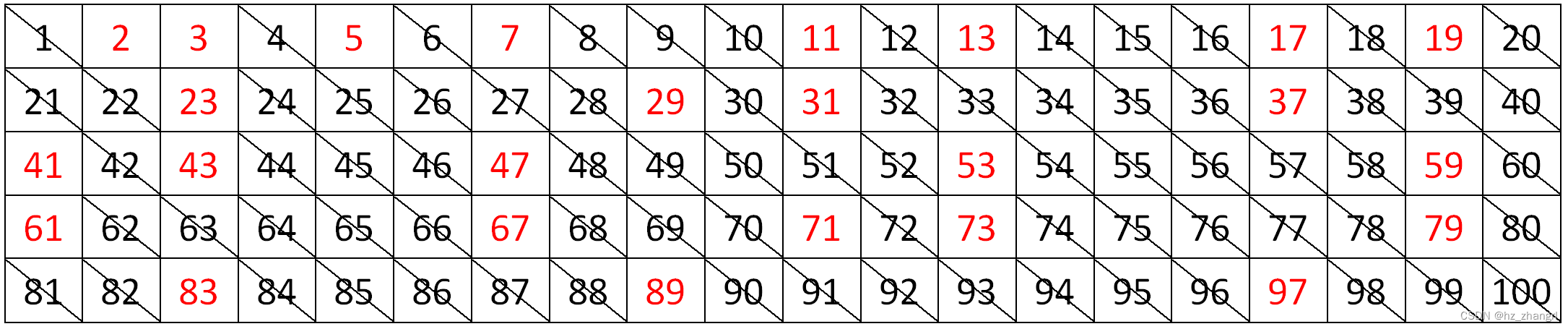
图1 埃氏筛原理图,求100以内的素数
若a为合数,则a能被表示成a=pq,其中p,q>1。易证p、q中一定有一个不超过(若p、q都超过
,则有a<pq)。更严格地,若a为合数,则一定存在质数p|a,且p≤
。
所以只需要用不超过10的全部质数(2,3,5,7)找出,然后删去它们在100以内的所有倍数(2的倍数,3的倍数,5的倍数,7的倍数),就删去了所有100以内的合数,剩下的就是100以内的质数。代码如下:
求n以内的所有素数的时间复杂度:O(nlog(logn))
def Eratosthene_sieve(n): # 埃氏筛法求2到n范围内所有素数
es = []
Td = [1] * (n + 1) # 0~n,n+1个元素
for i in range(2, n + 1):
if Td[i]:
es.append(i)
for j in range(i ** 2, n + 1, i):
Td[j] = 0
return es
P = Eratosthene_sieve(10**8): # 求10⁸以内的素数
print(P)更快的埃氏筛法:
def Eratosthene_sieve(n):
P = []
f = []
for i in range(n + 1): # 可以用f=[1]*(n+1)初始化f, f有n+1个元素(0-n)
if i > 2 and i % 2 == 0: # 此处在初始化时同时筛除了2的倍数,一半被筛
f.append(1)
else:
f.append(0)
i = 3
while i * i <= n: # 用3~n**0.5进行筛
if f[i] == 0:
j = i * i
while j <= n:
f[j] = 1
j += i + i
i += 2
P.append(2) # 将素数放入列表P中
for x in range(3, n + 1):
if f[x] == 0:
P.append(x)
return P
P = Eratosthene_sieve(10**8): # 求10⁸以内的素数
print(P)更绝的埃氏筛法:
充分利用Python的特色操作:列表生成式和切片操作。
def Eratosthene_sieve(n): # 埃氏筛法求2到n范围内所有素数
es = [i for i in range(2, n+1)]
L=len(es)
for i in range(L):
p = es[i]
if p != 0:
es[i+p:L:p] = [0]*len(es[i+p:L:p])
es = list(filter(lambda x: x != 0, es))
return es
P = Eratosthene_sieve(10**8): # 求10⁸以内的素数
print(P)四、用欧拉筛法优化
埃氏筛法会重复筛,增加时间复杂度,为了更优化,将使用欧拉筛。
欧拉筛法(Euler sieve method):在埃氏筛的基础上(也是用素数的倍数去筛掉非素数,合数只能被它的最小质因数来筛,比如20 ,只能用它的最小质因数2来筛除,不能用4、或者5去筛除)。
不同于埃氏筛的是欧拉筛不会重复筛一个数,从而降低了时间的复杂度。
欧拉筛的核心就是 if I % p[j]==0: break,代码如下:
欧拉筛法的时间复杂度为O(n)。
def euler_sieve(n):
f = [1] * (n + 1)
p = []
for i in range(2, n + 1):
if f[i]:
p.append(i)
for j in range(len(p)):
if i* p[j] > n:
break
f[i * p[j]] = 0
if i % p[j] == 0:
break
return p
P = euler_sieve(10**8): # 求10⁸以内的素数
print(P)测试以上各种算法的正确性时,可以将n值设置得小一点,将各例子中的10**8改为10**4,否则print(P)执行时间会非常长。测试以上各种算法各自的执行效率时,请删除print(P),或将 print(P)改为print(len(P)),并请自行加上时间模块,记录起始时间和结束时间,求时间差。