机器学习中常用的数学公式推导（概率论与数理统计）

常用的概念：
微积分是研究变量的数学，概率论是研究随机变量的数学。
研究一个随机变量，不只是要看它能取哪些值，更重要的是它取各种值的概率如何！
离散：
离散型随机变量：随机变量的值可以逐个列举出来。
概率函数：概率函数，就是用函数的形式来表达概率。如pi=P(X=ai)(i=1,2,3,4,5,6)
从公式上来看，概率函数一次只能表示一个取值的概率。比如P（X=1）=1/6,这代表用概率函数的形式来表示，当随机变量取值为1的概率为1/6，一次只能代表一个随机变量的取值。
概率分布： X的全部取值和P的全部取值
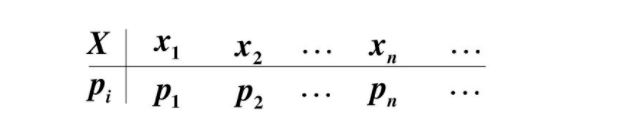分布函数：它是概率函数取值累加的结果。
连续：
连续性随机变量：随机变量的值无法逐个列举出来。
左边是F(x)连续型随机变量分布函数画出的图形，右边是f(x)连续型随机变量的概率密度函数画出的图像，它们之间的关系就是，概率密度函数是分布函数的导函数。
用右图来表示概率，就能清楚的看出，那些取值的概率更大。

期望：在概率论和统计学中，数学期望(mean)（或均值，亦简称期望）是试验中每次可能结果的概率乘以其结果的总和，是最基本的数学特征之一。它反映随机变量平均取值的大小。
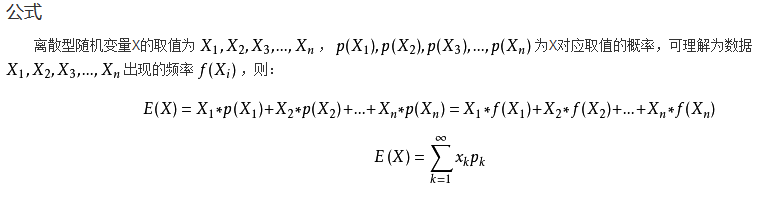方差：方差是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。概率论中方差用来度量随机变量和其数学期望（即均值）之间的偏离程度。

一、正态分布
$f(x) = \frac{1}{{\sqrt {2\pi } \delta }}\exp \left( { - \frac{{{{\left( {x - \mu } \right)}^2}}}{{2{\delta ^2}}}} \right)$ 一般正态分布
$f(x) = \frac{1}{{\sqrt {2\pi } }}\exp \left( { - \frac{{{x^2}}}{2}} \right)$标准正态分布
一般正态分布化标准正态分布
$p(x < k) = \int_{ - \infty }^k {\frac{1}{{\sqrt {2\pi } \delta }}} \exp \left(- {\frac{{{{\left( {x - u} \right)}^2}}}{{2{\delta ^2}}}} \right)$
$\begin{array}{l} x = z\delta + \mu \\ dx = \delta dz \end{array}$
可得标准正态分布
$p(z < k) = \int_{ - \infty }^k {\frac{1}{{\sqrt {2\pi } \delta }}} \exp \left( { - \frac{{{{\left( {z\delta } \right)}^2}}}{{2{\delta ^2}}}} \right)\delta dz = \int_{ - \infty }^k {\frac{1}{{\sqrt {2\pi } }}} \exp \left( { - \frac{{{z^2}}}{2}} \right)dz$
性质：

μ是正态分布的位置参数，描述正态分布的集中趋势位置。概率规律为取与μ邻近的值的概率大，而取离μ越远的值的概率越小。正态分布以X=μ为对称轴，左右完全对称。正态分布的期望、均数、中位数、众数相同，均等于μ。
σ描述正态分布资料数据分布的离散程度，σ越大，数据分布越分散，σ越小，数据分布越集中。也称为是正态分布的形状参数，σ越大，曲线越扁平，反之，σ越小，曲线越瘦高。
二、卡方分布

watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2RyZWFtZV9saWZl,size_16,color_FFFFFF,t_70)
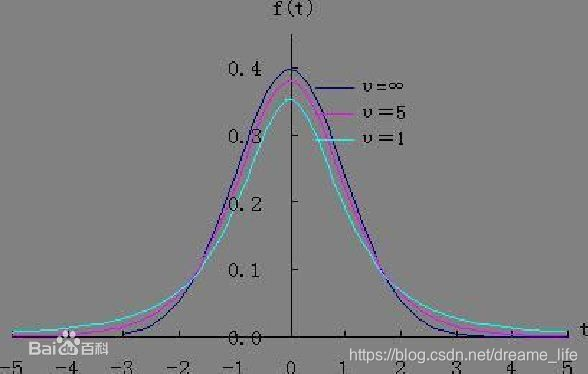
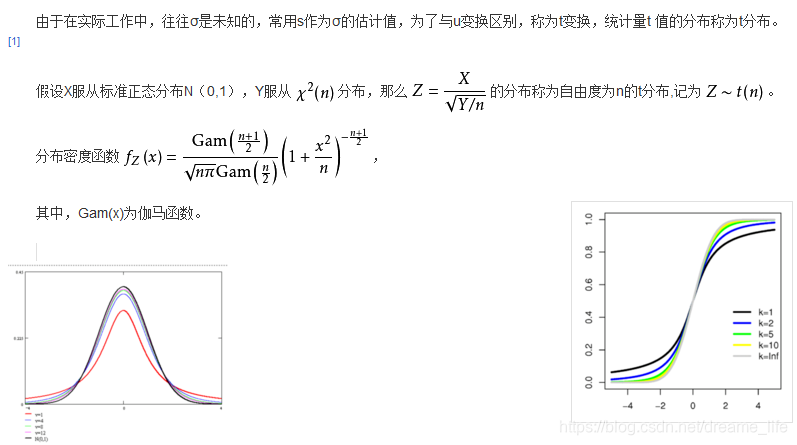
三、t-分布
百度定义如下：
在概率论和统计学中，学生t-分布（t-distribution），可简称为t分布，用于根据小样本来估计呈正态分布且方差未知的总体的均值。如果总体方差已知（例如在样本数量足够多时），则应该用正态分布来估计总体均值。
t分布曲线形态与n（确切地说与自由度df）大小有关。与标准正态分布曲线相比，自由度df越小，t分布曲线愈平坦，曲线中间愈低，曲线双侧尾部翘得愈高；自由度df愈大，t分布曲线愈接近正态分布曲线，当自由度df=∞时，t分布曲线为标准正态分布曲线。
四、极大似然法
设总体X是离散型随机变量，其概率函数为p(x, θ)，其中θ是未知参数。设X1,X2,…,Xn为取自总体X的样本，则可求出X1,X2,…,Xn的联合概率函数。如果样本取值x1,x2,…,xn，则事件(X1=x1,X2=x2,…,Xn=xn)发生的概率是为可求，这一概率值随θ的值的变化而变化，从直观上来看，既然样本值x1,x2,…,xn已经出现，它们出现的概率相对来说应比较大，应使其概率取比较大的值。极大似然法就是在参数θ的可能取值范围内，选取使L(θ)达到最大的参数值θ，作为参数θ的估计值。即取θ，使得L(θ)=L(x1,x2,…,xn; θ)=max(x1,x2,…,xn; θ)。 [1]
因此，求参数θ的极大似然估计值得问题就是求似然函数L(θ)最大值问题。通过解方程dL(θ)/dθ=0来得到，因为lnL(θ)和L(θ)的增减性相同，所以它们在θ的同一值处取得最大值，称lnL(θ)为对数似然函数，可以通过求解对数似然函数的最大值来得到极大似然解。