【算法】期望DP

概述

一般来说，概率DP找到正确的状态定义后，转移是比较容易想到的。但状态一定是“可数”的，把有范围的整数作为数组下标。事实上，将问题直接作为状态是最好的。如问“n人做X事的期望次数”，则设计状态为f[i]表示i个人做完事的期望。转移一般是递推，即从上一个状态转移得（填表）或转移向下一个状态（刷表）。

有时期望DP需以最终状态为初始状态转移，即逆推。如f[i]表示期望还要走f[i]步到达终点。这种状态的转移是刷表法，形如 $f[i]=∑p[i→j]f[j]+w[i→j]$，其中p[ ]表示转移的概率，w[ ]表示转移对答案的贡献。一般来说，初始状态确定时可用顺推，终止状态确定时可用逆推。

规律

1.期望可以分解成多个子期望的加权和，权为子期望发生的概率，即
$E(aA+bB+…) = aE(A) + bE(B) +…+1$；
2.期望从后往前找，一般 $dp[n]=0,dp[0]$是答案；
3.解决过程，找出各种情况乘上这种情况发生的概率，求和；
4.概率DP一定要初始化！

全概率公式

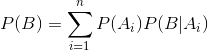
公式表示若事件A1，A2，…，An构成一个完备事件组且都有正概率，则对任意一个事件B都有公式成立。

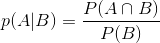
假如事件A与B相互独立，那么：

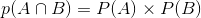
例题

1.UVA11021 Tribles麻球繁衍

UVA11021 Tribles麻球繁衍
题意翻译
题目大意
一开始有k种生物，这种生物只能活1天，死的时候有 $p_i$的概率产生ii只这种生物（也只能活一天），询问m天内所有生物都死的概率（包括m天前死亡的情况）
输入格式
第一行输入一个整数T，表示数据总数
每一组先输入三个整数n(1<=n<=1000),k(0<=k<=1000),m(0<=m<=1000)
然后输入n个整数，分别为 $p_0$到 $p_{n-1}$

对于每一组数据，先输出"Case #x: " 再输出答案，精度要求在1e-6以内

—————————————————————————————————————————

思路：每个麻球是互相独立的，设计状态f[i]表示一个麻球i天内死绝的概率，则n个麻球在i天内死亡的概率是 $f[i]^n$ 。转移时考虑这个麻球第一天繁衍多少个，它们在接下来的i−1天内死绝了。转移方程为 $f[i]=\sum_{j=0}^{k-1}p[j]f[i-1]^j$ ,
即 $f i ​ =p 0 ​ +p 1 ​ f i−1 ​ +p 2 ​ (f i−1 ​ ) 2 +p 3 ​ (f i−1 ​ ) 3 +...+p n−1 ​ (f i−1 ​ ) n−1$

其中 $p_{j}(f_{i-1})^{j}$的意思是，又生了j个麻球，这些麻球在i-1天后死亡。

由于一开始有k只麻球，且各麻球死亡是独立的，所以答案为 ${(f_{m}})^{k}$

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N=1e3+7;
const ll mod=1e9+7;
ll t,n,k,cnt,m;
double p[N];
double f[N];
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
    cin>>t;
    while(t--)
    {
        memset(f,0,sizeof f);
        memset(p,0,sizeof p);
        cnt++;
        cin>>n>>k>>m;
        for(int i=0;i<n;i++)
            cin>>p[i];
        f[1]=p[0];
        for(int i=2;i<=m;++i)
            for(int j=0;j<n;++j)
                f[i]+=pow(f[i-1],j)*p[j];
        printf("Case #%lld: %.7lf\n",cnt,pow(f[m],k));
    }
}

2.算概率（简单，数论）

算概率

说明：有 1 道题，做对的概率是 $1 \over 2$ 在模 $10^9+7$意义下为 500000004 ）。

$f i,j$表示前 i 道题做对 j道的概率转移时考虑第 j 道题是否做对，转移方程为：
$f_{i,j}=f_{i-1,j}\times (1-p_i)+f_{i-1,j-1}\times p_i$
时间复杂度 $O(n^2)$。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N=2e3+7;
const ll mod=1e9+7;
ll n,f[N][N],a[N];
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
    cin>>n;
    for(int i=1;i<=n;i++)
        cin>>a[i];
    for(int i=f[0][0]=1;i<=n;i++)
    {
        f[i][0]=f[i-1][0]*(mod+1-a[i])%mod;
        for(int j=1;j<=i;j++)
            f[i][j]=(f[i-1][j]*(mod+1-a[i])+f[i-1][j-1]*a[i])%mod;
    }
    for(int i=0;i<=n;i++)
        cout<<f[n][i]<<" ";
    cout<<endl;
    return 0;
}