八皇后问题(DFS和递归)

深度搜索的思想就是从初始状态出发，下一步可能有多种状态，选其中一个状态深入，到达新的状态；直到无法继续深入，退回到前一步，转移到其他状态，然后再深入下去。

先从一个例题开始看一下DFS递归的使用

排列数字

给定一个整数n，将数字1~n排成一排，将会有很多种排列方法。

现在，请你按照字典序将所有的排列方法输出。

输入格式
共一行，包含一个整数n。

输出格式
按字典序输出所有排列方案，每个方案占一行。

数据范围
1≤n≤7
输入样例：
3
输出样例：
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

#include<iostream> 
using namespace std;
const int N = 10;
int n;
int path[N];
bool st[N];

void dfs(int u)
{
	if(u == n)
	{
		for(int i = 0; i < n; i ++ ) cout<<path[i]<<" ";
		cout<<endl;
		return;
	}
	
	for(int i  = 1; i <= n; i ++ )
	{
		if( !st[i] )
		{
			path[u] = i;
			st[i] = true;
			dfs(u + 1);
			path[u] = 0;
			st[i] = false;
		}
	}
}

int main()
{
	cin>>n;
	dfs(0);
	return 0;
}

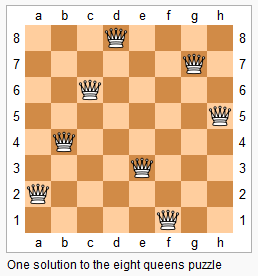
八皇后问题

在棋盘上放置8个皇后，使它/们互不攻击，此时每个皇后的攻击范围为同行同列和同对角线，所以不能让它们处于同行、同列和同对角线。输出所有情况的棋盘。**

• 由于很多子结点不符合条件，可以在递归时候中途停止并返回，这个思路就是回溯，在回溯中用于减少子结点扩展的部分叫剪枝。

当把问题分成若干步骤并递归求解时，如果当前步骤没有合法选择，则函数将返回上一级递归调用 ，这种现象称为回溯。正因为这个原因，递归枚举算法常被成为回溯法。

• 解决此问题的关键就是如何递归和回溯，难度主要在于扩展子结点的时候如何构造停止递归并返回的条件。

解题思路就是按行枚举Q, 然后递归出其他皇后。

---

n-皇后问题是指将 n 个皇后放在 n∗n 的国际象棋棋盘上，使得皇后不能相互攻击到，即任意两个皇后都不能处于同一行、同一列或同一斜线上。

现在给定整数n，请你输出所有的满足条件的棋子摆法。

输入格式
共一行，包含整数n。

输出格式
每个解决方案占n行，每行输出一个长度为n的字符串，用来表示完整的棋盘状态。

其中”.”表示某一个位置的方格状态为空，”Q”表示某一个位置的方格上摆着皇后。

每个方案输出完成后，输出一个空行。

数据范围
1≤n≤9
输入样例：
4
输出样例：
.Q…
…Q
Q…
…Q.

…Q.
Q…
…Q
.Q…

#include<iostream>
using namespace std;
const int N = 20;
int n;
char g[N][N];
bool col[N],dg[N],bdg[N];//列，对角线。反对角线

void dfs(int u)
{
	if(u == n)
	{
		for(int i = 0;i < n; i++) puts(g[i]);
		puts("");
		return;
	}
	for(int i  = 0;i < n; i ++)
		if(!col[i] && !dg[u + i] && !bdg[n - u + i])//剪枝
		{
			g[u][i] = 'Q';//枚举Q
			col[i] = dg[u + i] =bdg[n - u + i] = true;
			dfs(u + 1);
			col[i] = dg[u + i] = bdg[n - u + i] = false;
			g[u][i] = '.'; 	//恢复原状
		} 
}

int main()
{
	cin>>n;
	for(int i = 0; i < n; i++)
		for(int j = 0; j < n;j++)
			g[i][j]= '.';
			
	dfs(0);
	
	return 0;	
		
 } 

算法的复杂度：O( n ! ),每行每行的放皇后，复杂度O(n),检查冲突O(n).当n=10时，已经达千万数量级。当n > 11的n皇后问题，需要用新方法。

---