题目
给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
示例 1:
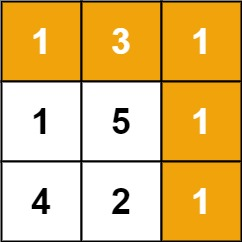
输入:grid = [[1,3,1],[1,5,1],[4,2,1]]
输出:7
解释:因为路径 1→3→1→1→1 的总和最小。
示例 2:
输入:grid = [[1,2,3],[4,5,6]]
输出:12
提示:
m == grid.length
n == grid[i].length
1 <= m, n <= 200
0 <= grid[i][j] <= 100
解题思路与算法
动态规划:
- 确定递推表达式:确定递推方程及其下标含义,dp[i][j]表示到第i行第j列的最短路径长度 ,dp[i][j]=Math.min(dp[i-1][j], dp[i][j-1])+grid[i][j];
- dp数组的初始化:对左上角元素初始化:dp[0][0]=grid[0][0];对第一列初始化:dp[i][0]=dp[i-1][0]+grid[i][0]; 对第一行初始化:dp[0][i]=dp[0][i-1]+grid[0][i];
- 由递推表达式得,顺序从左向右一层一层遍历
代码
class Solution {
public int minPathSum(int[][] grid) {
int m=grid.length;
int n=grid[0].length;
int [][] dp=new int[m][n];
dp[0][0]=grid[0][0];
for(int i=1;i<m;i++) {
dp[i][0]=dp[i-1][0]+grid[i][0];
}
for(int i=1;i<n;i++) {
dp[0][i]=dp[0][i-1]+grid[0][i];
}
for(int i=1;i<m;i++) {
for(int j=1;j<n;j++) {
dp[i][j]=Math.min(dp[i-1][j], dp[i][j-1])+grid[i][j];
}
}
return dp[m-1][n-1];
}
}