文章目录
1 参数方程
要求:理解

2 参数曲线的一般形式
要求:基函数,控制点,曲线方程,理解基函数和控制点关系
基函数:用一些简单多项式函数(基函数)组合出所需要的曲线曲面。这些函数都是标准化了的函数,与具体问题无关,是固定不变的。
控制点: 逼近法中所建立的曲线或曲面数学模型只是接近已知的点,而不要求一定通过。此时已知点称为控制点。
曲线方程:曲线方程就是标准基函数的加权和。
基函数和控制点关系:以控制点为权,将基函数组合在一起,使基函数叠加而形成曲线。控制点在组合过程中起到了调节系数的作用。
3 张量积形式的参数曲面
曲面方程可以看做是曲线方程增加维数,从一维扩展到二维得到的,这样构建的曲面称为张量积曲面。
控制点应在空间排列成方阵。沿u方向有n+1个,沿v方向有m+1个,共(n+1)*(m+1)个点。
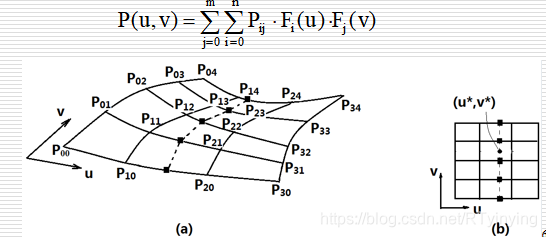
张量积曲面的优点:
(1)和曲线同构,仍然是使用控制点和基函数复合成;
(2)基函数仍然是曲线的基函数;
(3)方程结构简单,因此计算简单;
(4)由于和曲线基函数相同,构造方法相同,因此曲线的性质都可以推广到曲面上。
4 连续性的定义 参数连续性Ck
参数连续性用Ck表示,称为K阶参数连续,指的是P-和P+的K阶导数相同。
C0连续意味着P- = P+,即曲线在该点是连接在一起的。
C1连续意味着(P-)’ =( P+)’,即曲线在该点左右导数相同。
C2连续意味着(P-)’’ =( P+)’’,即曲线在该点左右二阶导数相同,切线从左侧平滑地过渡到右侧,两侧具有相同的曲率。
5 插值、逼近和拟合
思考:为什么要进行拟合
插值:插值 是对一组给定的已知点,这些点称为型值点,要求建立曲线或曲面数学模型,严格通过已知的每一个型值点。其数学模型称为插值曲线或插值曲面。
逼近:逼近法中所建立的曲线或曲面数学模型只是接近已知的点,而不要求一定通过。此时已知点称为控制点,因为它们虽然不在曲线上,但控制着曲线的形状。
拟合:插值和逼近统称为拟合,都是指设计中,基于已知的离散点生成的曲线或曲面,达到近似地表示物体形状的目的。
为什么要进行拟合:基于已知的离散点生成的曲线或曲面,达到近似地表示物体形状的目的
6 Bernstein多项式
要求:生成公式和性质,推导低次数解析函数
Bernstein多项式是一组多项式,包含n次多项式共n+1个。
一般性的数学公式如下:
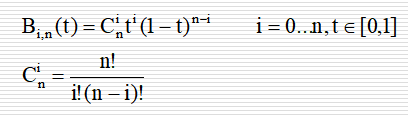
Bernstein多项式的性质:
(1)权性 和为1
(2)非负性
(3)端点性质
t=0时,第一个基函数值为1,其它为0。
t=1时,最后一个基函数值为1,其它为0。
(4)对称性
将t换为1-t,多项式仍相等。
(5)递推性
一个基函数可以从2个低一阶的基函数计算得到,公式为:
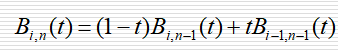

(6)导数
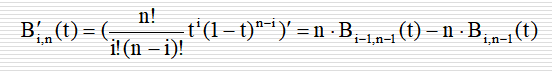
7 Bezier曲线及曲面,构造方法和性质,DeCasteljau算法
Bezier曲线
构造方法:
给出n+1个控制点P0、P1…Pn,构建Bezier参数曲线如下
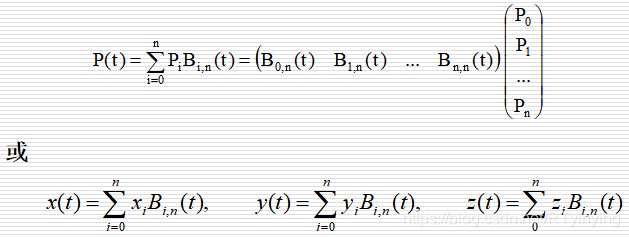
性质:
(1)与控制点的关系
曲线的起点与第一个控制点重合,曲线的终点与最后一个控制点重合,除此之外,曲线均不通过其它控制点。
(2)曲线次数与控制点相关
控制点的个数决定了曲线的次数。n+1个控制点,需要有n+1个基函数,根据Bernstein多项式的定义,基函数必然是n次多项式,曲线也就是n次曲线。而且在参数域,曲线的定义域为[0,1]
(3)凸包性
不计控制点次序,将控制点连接成一个最小凸多边形,称为控制多边形。因为Bernstein多项式总和为1 ,Bezier曲线全体落在控制多边形内。
(4)几何不变性
几何不变性指图形的某些性质不随坐标系的改变而变化。
Bezier曲线被控制多边形所确定,曲线形状决定于控制多边形的形状。改变坐标系时,并不改变控制多边形的形状,曲线也不会改变。
(5)端点导数
对Bezier曲线求导,有
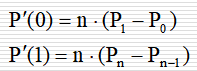
如果将控制点按顺序依次连成折线,曲线在第一个点处的切线,与第一段折线重合。最后一个点处的切线,与最后一段折线重合。

Bezier曲面
设Pij为(n+1)(m+1)个空间点阵列,则 n*m次张量积形式的Bezier曲面定义为
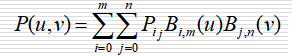
Bezier曲面是有界的,可称为Bezier曲面片。若使点阵中的点,首行与末行重复,或首列与末列重复,可以产生闭合的Bezier曲面
性质:
因为是张量积曲面,Bezier曲面的性质与Bezier曲线相似。
(1)端点和边界性质
Bezier曲面在四个角点上与控制点重合,不通过其它控制点。
(2)凸性
(3)几何不变性
(4)端点导数
角点三角形为Bezier曲面在角点的切平面。
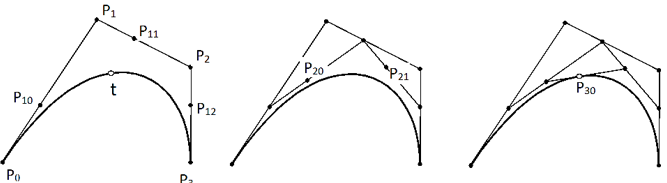
Casteljau算法
Casteljau构建了适合于任意次数Bezier曲线的快速算法。而且不涉及Bezier曲线的解析格式,只需要从控制点出发进行计算。
例题:
以4个控制点(P0,P1,P2,P3)的三次Bezier曲线为例,说明Casteljau算法的计算过程。 (t:1-t)

8 B样条基函数的Cox递推公式
要求:
1 B样条基函数为多项式函数,其中每个函数由规则产生,即Cox递推公式。
2 理解参数轴节点ui。
3 理解递推规则:两个k-1次函数,升阶得到k次函数。
4 理解基函数定义域(非0区间)为[ui,ui+k+1] 。
5 能推出低次数的基函数解析公式。
6 理解B样条曲线基函数性质。
Cox公式:
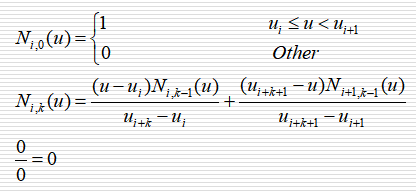

参数轴节点:
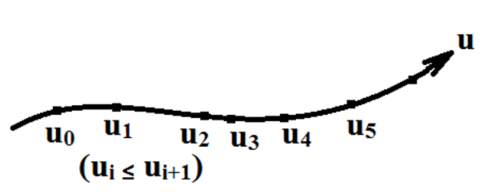
递推规则:两个k-1次函数,升阶得到k次函数。
基函数非0区间:[ui,ui+k+1]
低次数基函数解析公式:
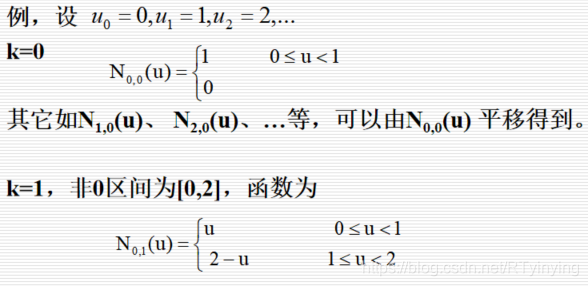


B样条曲线基函数性质:
(1)局部性
仅在k+1个节点区间非0。
(2)有界性
B样条基函数的函数值非负且小于1。即 0<=N0,1(u)<=1 。
(3)权性
如果将一个基函数的几段平移到一个区间,它们的和为1。
(4)对称性
B样条基函数的对称性指一个基函数中各段具有对称性。
(5)连续性
一个K次基函数在整体上能达到K-1次连续
9 B样条曲线
要求:
1 定义一条B样条曲线,需要给出:曲线次数、控制点、节点。
2 理解B样条曲线方程。
3 理解B样条曲线是分段曲线,每个节点区间定义一段曲线,且段间具有良好的连续性,k次曲线能达到k-1次连续。
4 理解分段曲线、控制点、基函数、节点区间的关系。
5 理解B样条曲线的性质。
k次B样条曲线方程:
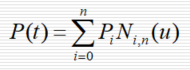
k次
n+1个控制点和基函数
n+1+k+1个节点
n+1-k个曲线段
曲线上每个点的计算涉及到k+1个控制点和基函数。
B样条曲线的性质:
(1)局部性
一个控制点最多能影响到k+1段曲线,改动一个控制点位置时,只影响控制点附近的曲线部分,对曲线的影响是局部的。由于曲线是分段生成的,增加或删除控制点的操作也便于进行。
(2)整体性和连续性
B样条曲线分段生成,但整体上,包括段间接合点在内,k次曲线能达到k-1次连续。
(3)几何不变性
在控制点相对位置不变的情况下,坐标变换不会影响曲线的整体形状。
(4)变差缩减性
平面内任意直线与P(t)的交点个数不多于该直线与其特征多边形的交点个数,反映了曲线比其特征多边形的波动小,更光顺。
(5)造型的灵活性
通过调节控制点和节点位置,能够灵活地调节曲线形状,也能产生特殊形状曲线。如尖点、直线等。举例如下:
2个控制点重合时,曲线相切与控制多边形。
4个控制点重合时,曲线在该处形成尖角;
4个顶点共线时产生含有直线段的曲线
(6)凸性
B样条曲线不通过任何控制点,整条曲线落在控制点形成的凸多边形内。
10 均匀B样条曲线
要求:
1 理解参数t情况下的均匀B样条基函数。
2 能推导出2、3次情况下的均匀B样条基函数。
3 均匀B样条曲线参数方程的定义。
如果节点在参数轴上均匀分布,所有节点区间均相同,这种情况下的B样条曲线称为均匀B样条曲线。一般常取整数点作为节点,即u0=0,u1=1,…un=n
均匀B样条曲线参数方程
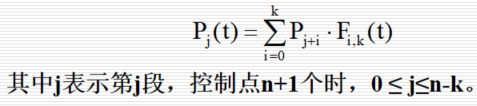
2次情况下的均匀B样条基函数
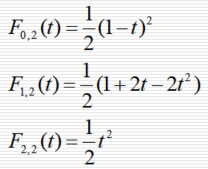
3次情况下的均匀B样条基函数
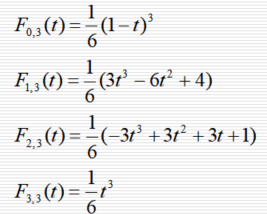

11 准均匀和非均匀B样条曲线
要求:
1 什么情况下形成准均匀和非均匀B样条曲线。
2 准均匀和非均匀B样条曲线的节点如何给出。
准均匀B样条曲线
在节点均匀分布的情况下,若允许部分或全部节点重复若干次,则成为准均匀B样条曲线,节点重复的次数称为重复度。
若两端节点具有重复度k+1,那么和Bezier曲线情况相似,B样条曲线通过首末两个控制点。
非均匀B样条曲线
节点区间长度可以任意,只需满足ui+1-ui>=0,此时称为非均匀B样条曲线。
节点区间长度能够影响该区间所生成的曲线的弧长。加大节点区间长度,相应地曲线弧长也会增加,减小节点区间长度,相应地曲线弧长也会减小
12 非均匀有理B样条曲面(NURBS)
要求:
1 理解NURBS方程。
2 理解权因子ω的意义。
3 定义一个NURBS曲面,需要给出的参数:次数、控制点、节点、权因子。
4 理解NURBS如何退化到B样条曲面、B样条曲线、均匀B样条曲线。
5 理解NURBS曲面性质和优点。
NURBS曲面方程:
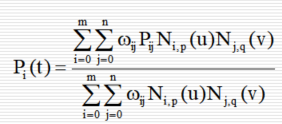

权因子:
增加了参数wij,是控制点的附加参数,和控制点在一起,称为权因子,每个控制点拥有一个。
控制点可以沿各个方向移动。
调节权因子只能使曲面上最接近控制点的点沿着接近控制点或远离控制点的直线上移动。而且调节权因子的影响范围比调节控制点的影响范围小,使得调节操作更为局部。可以认为是一个微调参数。
权因子的作用是对控制点向量的缩放
如何退化:
如果所有的w=1,定义式中的分母项就成为1,方程退化为B样条曲面。
如果网格只有一行控制点,就退化为B样条曲线。
NURBS曲面的性质:
(1)局部性
(2)凸包性
(3)几何不变性
(4)高节导数连续性
优点:
(1)造型能力强,可以精确地如二次曲面等标准形状。
(2)增加了曲面形状的权因子,便于实现相当复杂的。
(3)NURBS方法是B样条方法在四维空间的直接推广。
(4)在自由曲线技术中,NURBS曲面是最普遍的形式,包含了Bezier曲线曲面、B样条曲线曲面。
(5)有成熟的计算技术,计算稳定快速。
(6)应用广泛,如OpenGL、DirectX、3DMax、Maya等软件中,都包含NURBS曲面构建和编辑功能。
传送门
上一章:计算机图形学 第四章 图形变换
下一章:计算机图形学 第七章 光照计算和纹理映射