系列文章目录
自动控制理论(1)——自动控制理论概述
自动控制理论(2)——控制系统的数学模型(微分方程、传递函数
自动控制理论(3)——控制系统的数学模型(系统框图和信号流图
自动控制理论(4)——系统的时域性能指标和一阶系统的时域分析
文章目录
一、二阶系统数学模型
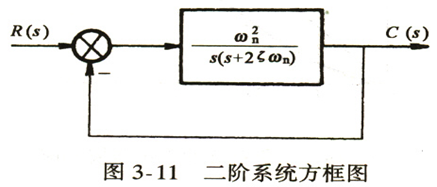
开环 G ( s ) = ω n 2 s ( s + 2 ζ ω n ) \ G(s)=\frac{ω_n^2}{s(s+2ζω_n)} G(s)=s(s+2ζωn)ωn2
闭环 ϕ ( s ) = ω n 2 s 2 + 2 ζ ω n s + ω n 2 \ ϕ(s)=\frac{ω_n^2}{s^2+2ζω_n s+ω_n^2 } ϕ(s)=s2+2ζωns+ωn2ωn2
特征方程 s 2 + 2 ζ ω n s + ω n 2 = 0 \ s^2+2ζω_n s+ω_n^2=0 s2+2ζωns+ωn2=0
ζ \ ζ ζ——阻尼比
ω n \ ω_n ωn——无阻尼自然振荡角频率
σ = ζ ω n \ σ=ζω_n σ=ζωn——衰减系数
ω d = ω n √ ( 1 − ζ 2 ) \ ω_d=ω_n √(1-ζ^2 ) ωd=ωn√(1−ζ2)——系统的阻尼振荡角频率
二、二阶系统单位阶跃响应
1. ζ = 0 \ ζ=0 ζ=0(零阻尼)
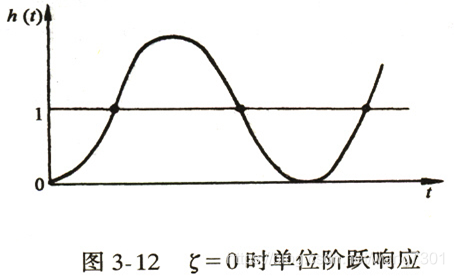
响应曲线为等幅振荡曲线。
2. ζ > 1 \ ζ>1 ζ>1( 过阻尼)
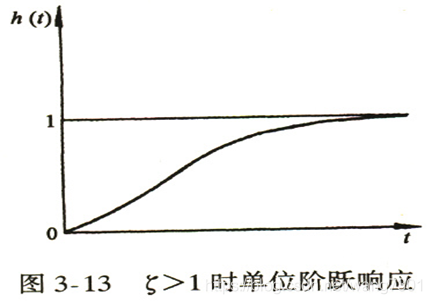
两个不等负实根
3. ζ = 1 \ ζ=1 ζ=1( 临界阻尼)
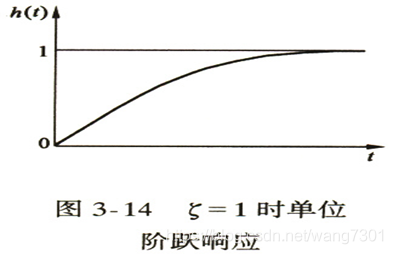
两个相等的负实根
4. 0 < ζ < 1 \ 0<ζ<1 0<ζ<1( 欠阻尼)
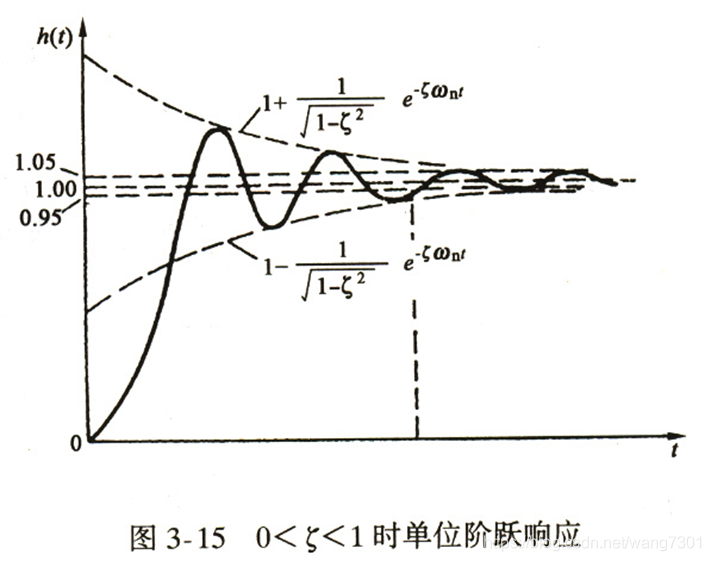
两个共轭复根 s 1 , 2 = − ζ ω n ± j ω n √ ( 1 − ζ 2 ) \ s_{1,2}=-ζω_n±jω_n √(1-ζ^2 ) s1,2=−ζωn±jωn√(1−ζ2)
阻尼角 β = t g − 1 √ ( 1 − ζ 2 ) ζ \ β=tg^{-1} \frac{√(1-ζ^2 )}{ζ} β=tg−1ζ√(1−ζ2)
5.总结

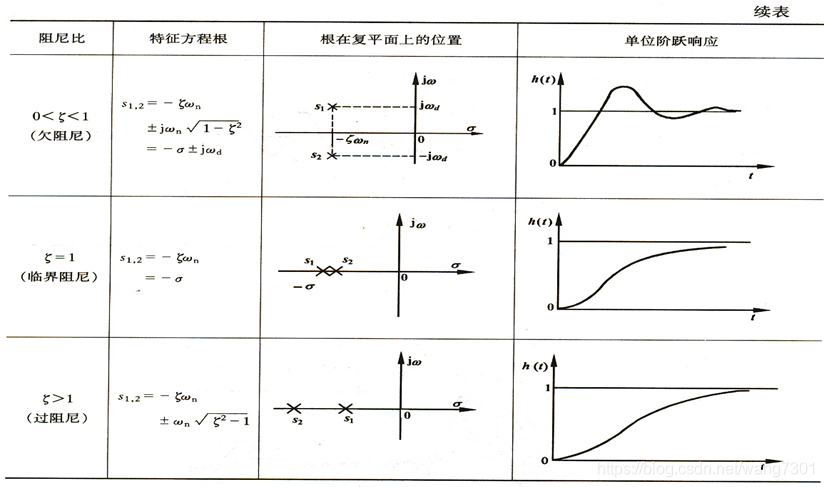

三 、欠阻尼二阶系统性能指标计算
1.上升时间 t r \ t_r tr
t r = π − β ω n √ ( 1 − ζ 2 ) \ t_r=\frac{π-β}{ω_n √(1-ζ^2 )} tr=ωn√(1−ζ2)π−β
阻尼比一定时,响应速度与 ω n \ ω_n ωn成正比;
阻尼振荡频率 ω d \ ω_d ωd一定时,阻尼比越小,上升时间越短。
2.峰值时间 t p \ t_p tp
t p = π ω n √ ( 1 − ζ 2 ) \ t_p=\frac{π}{ω_n √(1-ζ^2 )} tp=ωn√(1−ζ2)π
峰值时间与闭环极点的虚部成反比,闭环极点离负实轴越远,峰值时间越短。
3.超调量 σ % \ σ\% σ%
σ % = e − ζ π √ ( 1 − ζ 2 ) \ σ\%=e^{\frac{-ζπ}{√(1-ζ^2 )}} σ%=e√(1−ζ2)−ζπ
超调量只与阻尼比有关,阻尼越大,超调越小。
4.调节时间 t s \ t_s ts
t s = 4 ζ ω n \ t_s=\frac{4}{ζω_n } ts=ζωn4 ( Δ = 2 % \ Δ=2\% Δ=2%)
或 t s = 3 ζ ω n \ t_s=\frac{3}{ζω_n } ts=ζωn3 ( Δ = 5 % \ Δ=5\% Δ=5%)
5.延迟时间 t d \ t_d td
当 0 < ζ < 1 \ 0<ζ<1 0<ζ<1 时, t d = 1 + 0.7 ζ ω n \ t_d=\frac{1+0.7ζ}{ω_n } td=ωn1+0.7ζ
增大自然频率或减小阻尼比,可以减小延迟时间。
四 、具有零点的二阶系统分析
1、原系统条件不变时,附加一个闭环零点,将使二阶系统阶跃响应的超调量增大,上升时间和峰值时间减小
2、零点距离极点越近,上述影响越显著
3、零点距离虚轴很远时,零点影响可忽略