文章目录
前言
需要开通vip的题目暂时跳过
笔记导航
点击链接可跳转到所有刷题笔记的导航链接
581. 最短无序连续子数组
给定一个整数数组,你需要寻找一个连续的子数组,如果对这个子数组进行升序排序,那么整个数组都会变为升序排序。
你找到的子数组应是最短的,请输出它的长度。

-
解答
//方法1 public int findUnsortedSubarray(int[] nums) { int len = nums.length; int[] newNums = Arrays.copyOf(nums, len); Arrays.sort(nums); int start = 0; int end = -1; for(int i = 0;i < len;i++){ if(nums[i] != newNums[i]){ start = i; break; } } for(int i = len-1;i >=0;i--){ if(nums[i] != newNums[i]) { end = i; break; } } return end - start + 1; } //方法2 public int findUnsortedSubarray(int[] nums) { int min = nums[nums.length - 1]; int first = 0; for(int i = nums.length - 2; i >= 0; i--) { if(nums[i] < min) { min = nums[i]; } if(min != nums[i]) { first = i; } } int max = nums[0]; int second = -1; for(int i = 1; i < nums.length; i++){ if(nums[i] > max) { max = nums[i]; } if(max != nums[i]) { second = i; } } return second - first + 1; } -
分析
- 方法1
- 将数组进行排序。
- 原先数组从前往后 找到第一个和排序后 相同位置不一样的数字的位置。
- 同理从后往前找到第一个和排序后相同位置不一样的数字的位置。
- 这两个位置之间的数字就是要找到目标。
- 方法2
- 两个for循环,第一个for循环是为了找到子数组的左边界,从后往前遍历数组,记录最小值。若当前的数字不是最小值,那么就更新子数组的左边界。
- 第二个for循环是为了找到子数组的右边界,从前往后遍历数组,记录最大值。若当前的数字不是最大值,那么就更新子数组的右边界。
-
提交结果
方法1

方法2

583. 两个字符串的删除操作
给定两个单词 word1 和 word2,找到使得 word1 和 word2 相同所需的最小步数,每步可以删除任意一个字符串中的一个字符。

-
解答
//方法1 public int minDistance(String word1, String word2) { int[][] m = new int[word1.length() + 1][word2.length()+1]; return word1.length() + word2.length() - 2 * dfs(word1,word2,word1.length(),word2.length(),m); } public int dfs(String word1,String word2,int m,int n,int[][] memo){ if(m == 0 || n == 0)return 0; if(memo[m][n] > 0)return memo[m][n]; if(word1.charAt(m-1) == word2.charAt(n-1)){ memo[m][n] = dfs(word1,word2,m - 1,n - 1,memo) + 1; return memo[m][n]; } memo[m][n] = Math.max(dfs(word1,word2,m - 1,n,memo),dfs(word1,word2,m,n - 1,memo)); return memo[m][n]; } //动态规划 public int minDistance(String word1, String word2) { int len1 = word1.length(); int len2 = word2.length(); int[][] dp = new int[len1 + 1][len2+1]; for(int i = 1;i <=len1;i++){ for(int j = 1;j <= len2;j++){ if(word1.charAt(i-1) == word2.charAt(j-1)){ dp[i][j] = dp[i-1][j-1] + 1; }else{ dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1]); } } } return len1 + len2 - 2 * dp[len1][len2]; } -
分析
-
方法1 记忆化递归
-
寻找两个字符串的最长公共子序列。
-
要删除的字符的个数 就是两个字符串长度之和 减去 2倍的最长公共子序列的长度。
-
递归的实现 寻找最长公共子序列的长度。
-
当word1.charAt(m-1) == word2.charAt(n-1)时,说明找到了相同的字符,那么递归的去寻找word1 前m-1个字符 和word2前n-1个字符中的最长公共子序列。
-
若不相等,则有两种情况,第一种是m向前挪一位,第二种是n向前挪一位,两者的结果中的最大值,就是word1前m个字符 和word2前n个字符中 的最长公共子序列。
-
用记忆集 记录已经计算的结果,避免重复计算。
-
方法2 动态规划
-
将上述递归的过程 写成动态规划。
-
dp[i] [j] 表示word1的前i个字符和word2的前j个字符中最长公共子序列的长度。
-
动态转移方程
当word1.charAt(i - 1) == word2.charAt(j-1)的时候
dp[i] [j] = dp[i-1] [j-1] + 1;
否则
dp[i] [j] = Math.max(dp[i] [j-1] ,dp[i-1] [j])
-
dp[len1] [len2]就是最长公共子序列的长度。
-
结果就是两个字符串长度之和 减去 2倍的最长公共子序列的长度。
-
-
提交结果

587. 安装栅栏
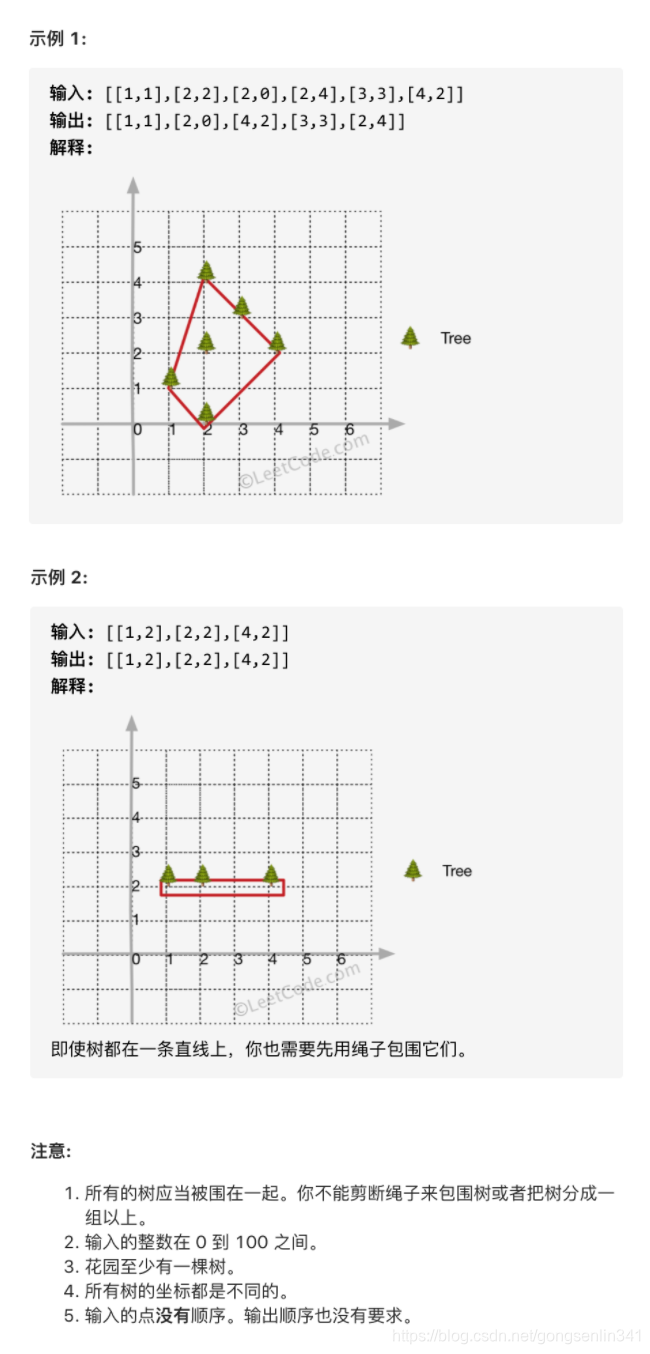
在一个二维的花园中,有一些用 (x, y) 坐标表示的树。由于安装费用十分昂贵,你的任务是先用最短的绳子围起所有的树。只有当所有的树都被绳子包围时,花园才能围好栅栏。你需要找到正好位于栅栏边界上的树的坐标。
-
解答
//方法1 public int[][] outerTrees(int[][] points) { Set<int[]> hull = new HashSet<>(); // 如果树的棵数小于 4 ,那么直接返回 if (points.length < 4) { for (int[] p : points) hull.add(p); return hull.toArray(new int[hull.size()][]); } // 找到最左边的点 int leftMost = 0; for (int i = 0; i < points.length; i++) { if (points[i][0] < points[leftMost][0]) leftMost = i; } int p = leftMost; do { int q = (p + 1) % points.length; for (int i = 0; i < points.length; i++) { // 如果 i 点在 pq 线下方,则使用 i 点 if (orientation(points[p], points[i], points[q]) < 0) q = i; } for (int i = 0; i < points.length; i++) { // p、q、i 在同一条线上的情况,并且 i 在 p 和 q 的中间的时候 // 也需要将这个点算进来 if (i != p && i != q && orientation(points[p], points[i], points[q]) == 0 && inBetween(points[p], points[i], points[q])) { hull.add(points[i]); } } hull.add(points[q]); // 重置 p 为 q,接着下一轮的遍历 p = q; } while (p != leftMost); return hull.toArray(new int[hull.size()][]); } // 以下 pq 和 qr 都是向量 // pq * qr > 0 表示 r 点在 pq 线上方 // pq * qr < 0 表示 r 点在 pq 线下方 // pq * qr = 0 表示 p、q、r 一条线 // |(q[0]-p[0]) (q[1]-p[1])| // pq * qr = | | = (q[0]-p[0]) * (r[1]-q[1]) - (r[0]-q[0]) * (q[1]-p[1]) // |(r[0]-q[0]) (r[1]-q[1])| private int orientation(int[] p, int[] r, int[] q) { return (q[0] - p[0]) * (r[1] - q[1]) - (r[0] - q[0]) * (q[1] - p[1]); } // 判断 r 点是不是在 p 点和 q 点之间,需要考虑以下两种情况: // 1. q 点在 p 点的左边或者右边 // 2. q 点在 p 点的上边或者下边 private boolean inBetween(int[] p, int[] r, int[] q) { boolean a = r[0] >= p[0] && r[0] <= q[0] || r[0] <= p[0] && r[0] >= q[0]; boolean b = r[1] >= p[1] && r[1] <= q[1] || r[1] <= p[1] && r[1] >= q[1]; return a && b; } -
分析
- 方法1
- 找到最左边的点开始
- 每次加入到集合中的点是相对于点p,逆时针最靠下的点q
- 找到点q后,判断有没有点 在p和q的连线上。
- pq * qr < 0 说明r点在pq下方,逆时针更靠下
- pq * qr = 0 说明r在pq方向上
- pq * qr > 0 说明r点在pq上方
- 直到q回到了最左边的点,结束while
-
提交结果
589. N叉树的前序遍历
给定一个 N 叉树,返回其节点值的前序遍历。
例如,给定一个 3叉树 :
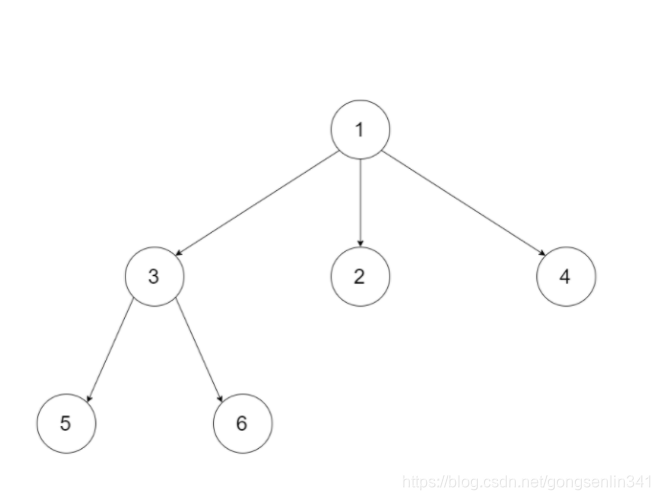
返回其前序遍历: [1,3,5,6,2,4]。
说明: 递归法很简单,你可以使用迭代法完成此题吗?
-
解答
List<Integer> res = new ArrayList<>(); if(root == null) return res; Stack<Node> stack = new Stack<>(); stack.push(root); while(!stack.isEmpty()){ Node cur = stack.pop(); res.add(cur.val); List<Node> children = cur.children; for(int i = children.size()-1;i >=0;i--){ stack.push(children.get(i)); } } return res; -
分析
- 非递归方法
- 和二叉树的前序遍历一样,利用栈来实现
- 对于出栈的结点,孩子入栈的顺序从右开始。
-
提交结果

590. N叉树的后序遍历
给定一个 N 叉树,返回其节点值的后序遍历。
例如,给定一个 3叉树 :
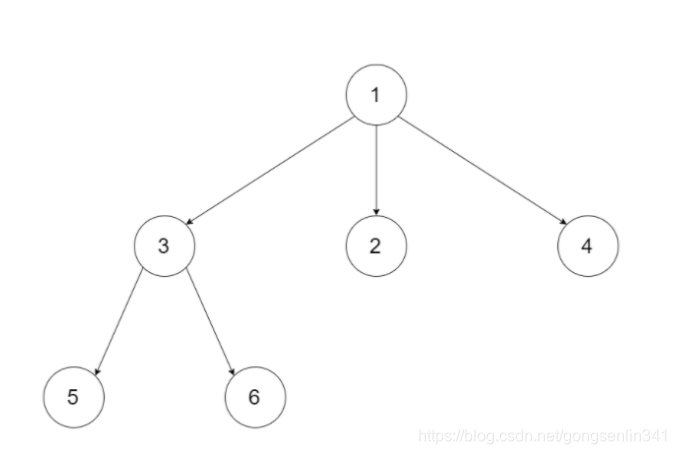
返回其后序遍历: [5,6,3,2,4,1].
说明: 递归法很简单,你可以使用迭代法完成此题吗?
-
解答
public List<Integer> postorder(Node root) { List<Integer> res = new ArrayList<>(); if(root == null)return res; Stack<Node> s1 = new Stack<>(); Stack<Node> s2 = new Stack<>(); s1.push(root); while(!s1.isEmpty()){ Node cur = s1.pop(); s2.push(cur); for(Node c : cur.children){ s1.push(c); } } while(!s2.isEmpty()){ res.add(s2.pop().val); } return res; } -
分析
- 非递归实现
- 和二叉树的后序遍历一样,使用双栈来实现。
-
提交结果

591. 标签验证器
给定一个表示代码片段的字符串,你需要实现一个验证器来解析这段代码,并返回它是否合法。合法的代码片段需要遵守以下的所有规则:
- 代码必须被合法的闭合标签包围。否则,代码是无效的。
- 闭合标签(不一定合法)要严格符合格式:<TAG_NAME>TAG_CONTENT</TAG_NAME>。其中,<TAG_NAME>是起始标签,</TAG_NAME>是结束标签。起始和结束标签中的 TAG_NAME 应当相同。当且仅当 TAG_NAME 和 TAG_CONTENT 都是合法的,闭合标签才是合法的。
- 合法的 TAG_NAME 仅含有大写字母,长度在范围 [1,9] 之间。否则,该 TAG_NAME 是不合法的。
- 合法的 TAG_CONTENT 可以包含其他合法的闭合标签,cdata (请参考规则7)和任意字符(注意参考规则1)除了不匹配的<、不匹配的起始和结束标签、不匹配的或带有不合法 TAG_NAME 的闭合标签。否则,TAG_CONTENT 是不合法的。
- 一个起始标签,如果没有具有相同 TAG_NAME 的结束标签与之匹配,是不合法的。反之亦然。不过,你也需要考虑标签嵌套的问题。
- 一个<,如果你找不到一个后续的>与之匹配,是不合法的。并且当你找到一个<或</时,所有直到下一个>的前的字符,都应当被解析为 TAG_NAME(不一定合法)。
cdata 有如下格式:<![CDATA[CDATA_CONTENT]]> - CDATA_CONTENT 的范围被定义成 <![CDATA[ 和后续的第一个 ]]>之间的字符。
- CDATA_CONTENT 可以包含任意字符。cdata 的功能是阻止验证器解析CDATA_CONTENT,所以即使其中有一些字符可以被解析为标签(无论合法还是不合法),也应该将它们视为常规字符。
合法代码的例子:



-
解答
Stack < String > stack = new Stack < > (); boolean contains_tag = false; public boolean isValidTagName(String s, boolean ending) { if (s.length() < 1 || s.length() > 9) return false; for (int i = 0; i < s.length(); i++) { if (!Character.isUpperCase(s.charAt(i))) return false; } if (ending) { if (!stack.isEmpty() && stack.peek().equals(s)) stack.pop(); else return false; } else { contains_tag = true; stack.push(s); } return true; } public boolean isValidCdata(String s) { return s.indexOf("[CDATA[") == 0; } public boolean isValid(String code) { if (code.charAt(0) != '<' || code.charAt(code.length() - 1) != '>')//若开头不是'<'或结尾不是'>'直接返回false return false; for (int i = 0; i < code.length(); i++) { //遍历字符串 boolean ending = false; int closeindex; if(stack.isEmpty() && contains_tag) return false; if (code.charAt(i) == '<') { if (!stack.isEmpty() && code.charAt(i + 1) == '!') { closeindex = code.indexOf("]]>", i + 1); if (closeindex < 0 || !isValidCdata(code.substring(i + 2, closeindex))) return false; } else { if (code.charAt(i + 1) == '/') { i++; ending = true; } closeindex = code.indexOf('>', i + 1); if (closeindex < 0 || !isValidTagName(code.substring(i + 1, closeindex), ending)) return false; } i = closeindex; } } return stack.isEmpty() && contains_tag; } -
分析
-
栈来实现
从代码的起始位置遍历整个代码片段。当我们发现 < 时,如果我们目前不在 cdata 的范围内,那么我们必须解析这个 <,即接下来一定是一个标签(起始标签或结束标签)或者一段 cdata。如果 < 后面接着的是 !,那么后面一定是一段 cdata,接下来必须匹配到 [CDATA[。在这之后,我们就可以遍历代码片段直到遇到 ]]>,表示 cdata 的结束,这中间的所有特殊符号我们都不需要解析。
如果 < 后面接着的不是 !,那么它一定是一个标签。如果是 </ 那么它是结束标签,否则是开始标签。我们继续遍历代码片段,直到遇到 > 表示标签的结束为止。此时 < 或 </ 与 > 之间的部分就是 TAG_NAME,我们需要检查 TAG_NAME 的合法性。如果它是一个起始标签,我们会把 TAG_NAME 入栈,如果它是一个结束标签,我们需要检查 TAG_NAME 和栈顶的元素是否相同。如果不相同或者栈为空,那么这就是一个不合法的结束标签。
在代码片段遍历结束后,我们还需要检查两点:第一是栈是否为空,如果不为空,说明还有未闭合的标签;第二是代码片段是否被合法的闭合标签包围,我们需要保证在第一个起始标签被闭合后,接下来不会有任何代码,并且每个 cdata 必须在栈不为空的时候才能出现。
-
-
提交结果

592. 分数加减运算
给定一个表示分数加减运算表达式的字符串,你需要返回一个字符串形式的计算结果。 这个结果应该是不可约分的分数,即最简分数。 如果最终结果是一个整数,例如 2,你需要将它转换成分数形式,其分母为 1。所以在上述例子中, 2 应该被转换为 2/1。

-
解答
public String fractionAddition(String expression) { String res = ""+expression.charAt(0); int len = expression.length(); int i = 1; for(i = 1;i < len;i++){ char cur = expression.charAt(i); if(cur == '-' || cur == '+')break; res += expression.charAt(i); } if(i == len)return expression; String second = ""; for(;i<len;i++){ char cur = expression.charAt(i); if(second.length() > 1 && (cur == '-' || cur == '+')){ res = cal(res,second); second = ""+cur; continue; } second += cur; } res = cal(res,second); return res; } public int gcd(int p,int q){ if(q == 0)return p; int r = p % q; return gcd(q,r); } public String cal(String s1,String s2){ boolean flagS1 = false; boolean flagS2 = false; if(s1.charAt(0)!= '-'){ flagS1 = true; if(s1.charAt(0) == '+') s1 = s1.substring(1); }else{ s1 = s1.substring(1); } if(s2.charAt(0)!= '-'){ flagS2 = true; if(s2.charAt(0) == '+') s2 = s2.substring(1); }else{ s2 = s2.substring(1); } String[] str1 = s1.split("/"); String[] str2 = s2.split("/"); int s1fenzi = Integer.valueOf(str1[0]); int s1fenmu = Integer.valueOf(str1[1]); int s2fenzi = Integer.valueOf(str2[0]); int s2fenmu = Integer.valueOf(str2[1]); int newfenmu = s1fenmu * s2fenmu / gcd(s1fenmu,s2fenmu); s1fenzi = newfenmu / s1fenmu * s1fenzi; s2fenzi = newfenmu / s2fenmu * s2fenzi; int newfenzi = 0; boolean flag = false; if(flagS1 != flagS2){ if(s1fenzi >= s2fenzi){ if(flagS1 || s1fenzi == s2fenzi) flag = true; newfenzi = s1fenzi - s2fenzi; }else{ if(flagS2) flag = true; newfenzi = s2fenzi - s1fenzi; } }else{ if(flagS1) flag = true; newfenzi = s1fenzi + s2fenzi; } int g = gcd(newfenmu,newfenzi); newfenmu /= g; newfenzi /= g; if(flag)return newfenzi + "/" + newfenmu; else return "-" + newfenzi +"/" + newfenmu; } -
分析
- 按照提议,划分出分数,逐个通分,然后计算即可。
-
提交结果

593. 有效的正方形
给定二维空间中四点的坐标,返回四点是否可以构造一个正方形。
一个点的坐标(x,y)由一个有两个整数的整数数组表示。

-
解答
public double dist(int[] p1, int[] p2) { return (p2[1] - p1[1]) * (p2[1] - p1[1]) + (p2[0] - p1[0]) * (p2[0] - p1[0]); } public boolean validSquare(int[] p1, int[] p2, int[] p3, int[] p4) { int[][] p={ p1,p2,p3,p4}; Arrays.sort(p, (l1, l2) -> l2[0] == l1[0] ? l1[1] - l2[1] : l1[0] - l2[0]); return dist(p[0], p[1]) != 0 && dist(p[0], p[1]) == dist(p[1], p[3]) && dist(p[1], p[3]) == dist(p[3], p[2]) && dist(p[3], p[2]) == dist(p[2], p[0]) && dist(p[0],p[3])==dist(p[1],p[2]); } -
分析
- 满足正方向的条件是,4边长度相等,切对角线长度相等。
- 先根据x为第一键,y为第二键来升序的排序4个角。这样就确定了4个角的相对位置。然后就是比较4边是否相等,以及对角线是否相等。
-
提交结果

594. 最长和谐子序列
和谐数组是指一个数组里元素的最大值和最小值之间的差别正好是1。
现在,给定一个整数数组,你需要在所有可能的子序列中找到最长的和谐子序列的长度。

-
解答
//方法1 public int findLHS(int[] nums) { if(nums.length == 0) return 0; Arrays.sort(nums); Map<Integer,Integer> map = new HashMap<>(); int res = 0; for(int i = 0;i < nums.length;i++){ int cur = nums[i]; if(map.containsKey(cur-1)){ map.put(cur-1,map.get(cur-1)+1); res = Math.max(res,map.get(cur-1)); } if(map.containsKey(cur)){ map.put(cur,map.get(cur)+1); }else{ map.put(cur,1); } } return res; } //方法2 public int findLHS(int[] nums) { HashMap < Integer, Integer > map = new HashMap < > (); int res = 0; for (int num: nums) { map.put(num, map.getOrDefault(num, 0) + 1); if (map.containsKey(num + 1)) res = Math.max(res, map.get(num) + map.get(num + 1)); if (map.containsKey(num - 1)) res = Math.max(res, map.get(num) + map.get(num - 1)); } return res; } -
分析
-
方法1
-
先对数组进行排序
-
然后使用hashMap来记录当前数字为key,比当前数字差1 的数字个数+当前数字的个数作为value
-
map中记录的value的最大值 就是结果。
-
方法2
-
不用进行排序
-
hashMap记录数字出现的次数
-
一次遍历的同时,若map中存在num+1的key,那么则计算num 和num+1的个数,和res比较保留较大者
-
同理 若map中存在num-1 的key 那么则计算num 和 num-1的个数,和res比较保留较大者。
-
-
提交结果
方法1

方法2

598. 范围求和 II
给定一个初始元素全部为 0,大小为 m*n 的矩阵 M 以及在 M 上的一系列更新操作。
操作用二维数组表示,其中的每个操作用一个含有两个正整数 a 和 b 的数组表示,含义是将所有符合 0 <= i < a 以及 0 <= j < b 的元素 M[i][j] 的值都增加 1。
在执行给定的一系列操作后,你需要返回矩阵中含有最大整数的元素个数。

-
解答
public int maxCount(int m, int n, int[][] ops) { for(int i = 0;i < ops.length;i++){ m = Math.min(m,ops[i][0]); n = Math.min(n,ops[i][1]); } return m * n; } -
分析
- 每次的操作都是以左上角开始的,所以必定会覆盖左侧和上侧。
- 那么就遍历ops,记录下最小的左侧和上侧即可。
- 返回最小的左侧和上侧的乘积。
-
提交结果

599. 两个列表的最小索引总和
假设Andy和Doris想在晚餐时选择一家餐厅,并且他们都有一个表示最喜爱餐厅的列表,每个餐厅的名字用字符串表示。
你需要帮助他们用最少的索引和找出他们共同喜爱的餐厅。 如果答案不止一个,则输出所有答案并且不考虑顺序。 你可以假设总是存在一个答案。

-
解答
//方法1 暴力 public String[] findRestaurant(String[] list1, String[] list2) { int minIndex = Integer.MAX_VALUE; List<String> list = new ArrayList<>(); for(int i = 0;i < list1.length;i++){ for(int j = 0;j < list2.length;j++){ if(i + j > minIndex)break; if(list1[i].equals(list2[j])){ if(i + j < minIndex){ minIndex = i + j; list = new ArrayList<>(); list.add(list1[i]); }else if(i + j == minIndex){ list.add(list1[i]); } break; } } } return res.toArray(new String[res.size()]); } //方法2 public String[] findRestaurant(String[] list1, String[] list2) { HashMap < String, Integer > map = new HashMap < String, Integer > (); for (int i = 0; i < list1.length; i++) map.put(list1[i], i); List < String > res = new ArrayList < > (); int min_sum = Integer.MAX_VALUE, sum; for (int j = 0; j < list2.length && j <= min_sum; j++) { if (map.containsKey(list2[j])) { sum = j + map.get(list2[j]); if (sum < min_sum) { res.clear(); res.add(list2[j]); min_sum = sum; } else if (sum == min_sum) res.add(list2[j]); } } return res.toArray(new String[res.size()]); } -
分析
- 方法1 暴力
- 方法2
- 第一次遍历 key为字符串,value为索引
- 第二次遍历,判断map中是否有这个字符串,若有的话,计算索引和,和最小索引和进行比较。若小于已知索引和,那么久更新最小索引和,并清空res。添加新的字符串进去。若最小索引和和当前计算出的索引和相同,则将当前字符串添加到集合res当中
-
提交结果
方法1
方法2

600. 不含连续1的非负整数
给定一个正整数 n,找出小于或等于 n 的非负整数中,其二进制表示不包含 连续的1 的个数。

-
解答
public int findIntegers(int num) { int[] f = new int[32]; f[0] = 1; f[1] = 2; for (int i = 2; i < f.length; i++) f[i] = f[i - 1] + f[i - 2]; int i = 30, sum = 0, prev_bit = 0; while (i >= 0) { if ((num & (1 << i)) != 0) { sum += f[i]; if (prev_bit == 1) { sum--; break; } prev_bit = 1; } else prev_bit = 0; i--; } return sum + 1; } -
分析
- f[i]记录位数为i的二进制数中不包含连续1的个数。
- 可以发现满足f[i] = f[i-1] + f[i-2];
- 初始条件 f[0] = 1,f[1] = 2
- 但是题目要求考虑小于等于num的数,所以除了上面的结果
- [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-fYHysMUi-1609492496726)(/Users/gongsenlin/Library/Application Support/typora-user-images/截屏2020-12-30 上午9.48.26.png)]
- 除此之外需要处理num中连续1的情况

-
提交结果
