图神经网络（一）图信号处理与图卷积神经网络（5）图卷积神经网络

0. 概述

在学习了图滤波器定义的基础之上，本节我们来看看图信号处理中的卷积操作是如何定义的¹。给定两组$\text{G}$上的图信号${\mathbf{x}}_1$、${\mathbf{x}}_2$，其图卷积运算定义如下：
$${\mathbf{x}}_1\ast {\mathbf{x}}_2=\text{IGFT}(\text{GFT}({\mathbf{x}}_1)\odot \text{GFT}({\mathbf{x}}_2))$$其中$\odot$表示哈达玛积。这里的定义与我们在离散时间信号处理中的卷积的定义是一样的——时域中的卷积运算等价于频域中的乘法运算。

 我们对上式继续进行推导：
$$\begin{array}{rl}{\mathbf{x}}_1\ast {\mathbf{x}}_2& =V((V^{\text{T}}{\mathbf{x}}_1)\odot (V^{\text{T}}{\mathbf{x}}_2))\\ & =V({\tilde{\mathbf{x}}}_1\odot (V^{\text{T}}{\mathbf{x}}_2))\\ & =V(\text{diag}({\tilde{\mathbf{x}}}_1)(V^{\text{T}}{\mathbf{x}}_2))\\ & =(V\text{diag}({\tilde{\mathbf{x}}}_1)V^{\text{T}}){\mathbf{x}}_2\end{array}$$ 令$H_{{\tilde{\mathbf{x}}}_1}=V\text{diag}({\tilde{\mathbf{x}}}_1)V^{\text{T}}$，显然$H_{{\tilde{\mathbf{x}}}_1}$是一个图位移算子，其频率响应矩阵为${\mathbf{x}}_1$的频谱，于是可得：
$${\mathbf{x}}_1\ast {\mathbf{x}}_2=H_{{\tilde{\mathbf{x}}}_1}{\mathbf{x}}_2$$ 从上式可知，两组图信号的图卷积运算总能够转化为对应形式的图滤波运算，从这个层面上来看，图卷积等价于图滤波。后文中提到的图卷积运算都是特指上式右边的滤波形式，只与相对应的卷积信号，一般并不需要显式地表达出来。

 需要特别说明的是，前面所有的图信号处理的相关概念里的图信号都能被拓展到矩阵形式。设矩阵$X\in R^{N\times d}$，我们可以将$X$视为$d$组定义在图$\text{G}$上的图信号，于是我们称$X$为图信号矩阵，$d$为图信号的总通道数，$X_{:,j}$表示第$j$个通道上的图信号。例如，对$Y=HX$，我们可以理解成用图滤波器$H$对信号矩阵$X$每个通道的信号分别进行滤波操作，$X_{:,j}$对应的输出为图信号矩阵$Y$在第$j$个通道上的图信号$Y_{:,j}$。

 借鉴卷积神经网络在计算机视觉中的成功，将上述定义的图卷积运算推广到图数据的学习中去就成了一种自然而然的想法。接下来，我们将介绍这其中具有代表性的一些工作。

1. 对频率响应矩阵进行参数化

 既然图卷积操作等价于图滤波操作，而图滤波算子的核心在于频率响应矩阵，那么我们自然想到对频率响应矩阵进行参数话²，这样我们就可以定义如下神经网络层：
$$\begin{array}{rl}{X}^{\prime }& =\sigma (V\left[\begin{array}{ccc}{\theta }_1& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\theta }_N\end{array}\right]V^{\text{T}}X)\\ & =\sigma (V\text{diag}(\theta )V^{\text{T}}X)\\ & =\sigma (\Theta X)\end{array}$$
其中$\sigma (\cdot )$是激活函数，$\theta =[{\theta }_1,{\theta }_2,\dots ,{\theta }_N]$是需要学习的参数，$\Theta$是对应的需要学习的图滤波器，$X$是输入的图信号矩阵，$X^{\prime }$是输出的图信号矩阵。基本上这个思路可以按照图滤波操作的空域视角与频域视角去理解：

 (1) 从空域视角来看，盖层引入了一个自适应的图位移算子，通过学习的手段指导该算子的学习，从而完成对输入图信号的针对性变换操作。

 (2) 从频域角度来看，该层在$X$与$X^{\prime }$之间训练了一个可自适应的图滤波器，图滤波器的频率响应函数时怎样的，可以通过任务与数据之间的对应关系来进行监督学习。

 上述思路虽然简单易懂，但是也存在一个较大的问题：引入的学习参数过多，需要学习的参数量与图中的节点数一致，这在大规模图数据，比如上亿节点数规模的图中，极易发生过拟合问题。

 另外，在真实的图数据中，数据的有效信息通常都蕴含在低频段中，因此为图滤波器设置$N$个维度的自由度，且对每个频率都进行学习是没必要的。

2. 对多项式系数进行参数化

 同样，为了拟合任意的频率响应函数，我们也可以将拉普拉斯矩阵的多项式形式转化为一种可学习的形式，该思路在参考文献[3]³中被提出具体如下：
$$X^{\prime }=\sigma \left(V\right(\sum _{k=0}^K{\theta }_k{\Lambda }^k\left)V^{\text{T}}X\right)=\sigma (V\text{diag}(\Psi \theta )V^{\text{T}}X)$$
其中，$\theta =[{\theta }_1,{\theta }_2,\dots ,{\theta }_K]$是多项式系数向量，也是该网络层真正需要学习的参数，与前述方法不同的是，这个方法的参数量$K$可以自由控制。$K$越大，可拟合的频率响应函数的次数就越高，可以对应输入图信号矩阵与输出图信号矩阵之间复杂的类别关系；$K$越小，可拟合的频率响应函数的次数就越低，可以对应输入图信号矩阵与输出图信号矩阵之间简单的滤波关系。总的来说，一般设$K\ll N$，这将大大降低模型过拟合的风险。

3. 设计固定的图滤波器

 前述方法虽然大大降低了参数量，但却由于对矩阵特征扥接比较依赖而给计算带来了极高的复杂度。为了解决这个问题，在论文《Semi-supervised classification with graph convolutional networks》⁴中，作者对上式进行了限制，设$K=1$，则：
$$X^{\prime }=\sigma ({\theta }_{0}X+{\theta }_{1}LX)$$  令${\theta }_0={\theta }_1=\theta$，则：
$$X^{\prime }=\sigma (\theta (I+L)X)=\sigma (\theta \tilde{L}X)$$  需要注意的是，这里的$\theta$是一个标量，相当于对$\tilde{L}$的频率响应函数做了一个尺度变换，通常这种尺度变换在神经网络模型中会被归一化操作替代，因此，这个参数是不必要引入的，我们设$\theta =1$，然后就得到了一个固定的图滤波器$\tilde{L}$。

 为了加强网络学习时的数值稳定性，作者仿照正则拉普拉斯矩阵，对$\tilde{L}$也做了归一化处理。令$${\tilde{L}}_{\text{sym}}={\tilde{D}}^{-1/2}\tilde{A}{\tilde{D}}^{-1/2}，\tilde{A}=A+I，{\tilde{D}}_{ii}=\sum _j{\tilde{A}}_{ij}，$$我们称${\tilde{L}}_{\text{sym}}$为重新归一化形式的拉普拉斯矩阵。${\tilde{L}}_{\text{sym}}$的特征值范围为$(-1,1]$，可以有效防止多层网络优化时出现的梯度消失或爆炸的现象。

 为了加强网络的拟合能力，作者设计了一个参数化的权重矩阵$W$对输入的图信号矩阵进行放射变换，于是得到：
$$X^{\prime }=\sigma ({\tilde{L}}_{\text{sym}}XW)$$ 如果没有其他说明，我们称上式为图卷积层（GCN layer），以此为主体堆叠多层的神经网络模型称为图卷积模型（GCN）。

 图卷积层是对频率响应函数拟合形式上的极大简化，最后相应的图滤波器退化成了${\tilde{L}}_{\text{sym}}$，图卷积操作变成了${\tilde{L}}_{\text{sym}}X$。如果将$X$由信号矩阵的角色切换到特征矩阵上，由于${\tilde{L}}_{\text{sym}}$是一个图位移算子，依据矩阵乘法的行向量视角，${\tilde{L}}_{\text{sym}}X$的计算等价于对邻居节点的特征向量进行局和操作，于是图卷积层在节点层面的计算公式如下：
$${\mathbf{x}}_i=\sigma (\sum _{v_j\in N(v_i)}{\tilde{L}}_{\text{sym}}[i,j](W{\mathbf{x}}_j))$$

图1 空域视角滤波计算示意图

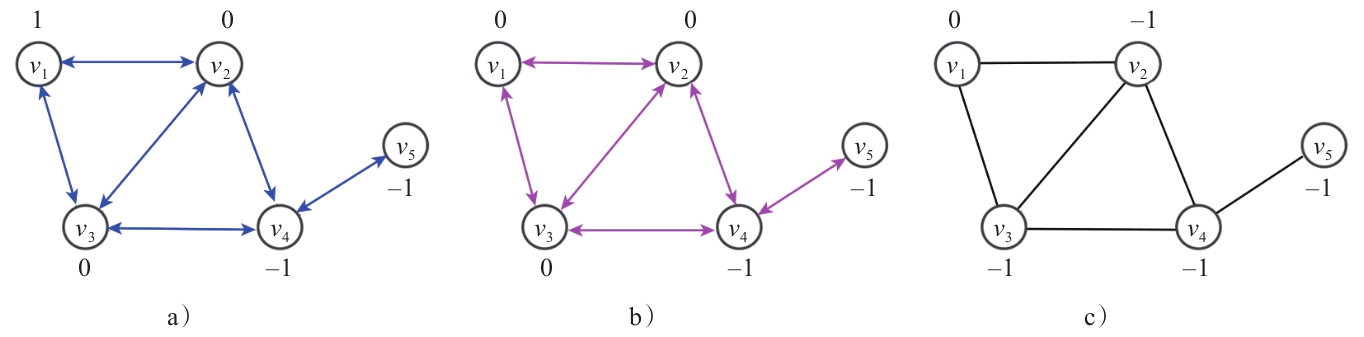
 图1即为这种聚合另据节点操作的示意图。实际在工程上，${\tilde{L}}_{\text{sym}}$可以用稀疏矩阵来表示，这可以进一步降低图卷积层的计算复杂度。相较于频域图卷积中矩阵分解时$O(N^3)$的时间复杂度，这种空域图卷积计算的时间复杂度可以降至$O(|E|d)$。

 至于在实际任务中设计固定图滤波器的做法是否有效，我们从以下两点进行说明：

 (1) ${\tilde{L}}_{\text{sym}}$本身所具有的的滤波特性是比较符合真实数据的特有性质的，能对数据实现搞笑的滤波操作；

 (2) 虽然GCN层是由对频率响应函数的线性近似推导得出来的，但是和深度学习中深度网络给模型带来的强大拟合能力一样，堆叠多层GCN层，在某种程度上，可以达到高阶多项式形式的频率响应函数的滤波能力。这种简化单层网络的学习能力，通过增加深度来提升模型表达能力的做法，在CNN模型中表现出了极强的工程优越性。事实证明明，这种设计所带来的优越性也在GCN后续的多项相关论文中得到了充分展示，以GCN为代表的模型俨然称为各类图数据学习任务的首选。

 总的来说，正式由于有了图信号处理中对图卷及操作的定义与理解，神经网络模型中的图卷积层才能得到非常直观的设计。一般来说，对于只能从频域出发进行矩阵分解特征从而执行图卷积计算的模型，我们称之为频域图卷积模型。相应地，对于图卷积计算不需要进行矩阵特征分解，能在空域视角执行矩阵乘法计算的模型，我们称之为空域图卷积模型。需要特别说明的是，虽然空域图卷积模型具有工程上的优越性，但是这类模型也都可以从频域视角进行理解，从本书后续的相关章节中，我们也可以看到频域视角对于图卷积模型的设计也是十分重要的。

参考文献

---

1. [1] 刘忠雨, 李彦霖, 周洋.《深入浅出图神经网络: GNN原理解析》.机械工业出版社. ↩︎

2. [2] Bruna J, Zaremba W, Szlam A, et al. Spectral networks and locally connected networks on graphs[J]. arXiv preprint arXiv:1312.6203, 2013. ↩︎

3. [3] Defferrard M, Bresson X, Vandergheynst P. Convolutional neural networks on graphs with fast localized spectral filtering[J]. Advances in neural information processing systems, 2016, 29. ↩︎

4. [4] Kipf T N, Welling M. Semi-supervised classification with graph convolutional networks[J]. arXiv preprint arXiv:1609.02907, 2016. ↩︎