一、Gabor 概述
1、Gabor 滤波器
该函数返回 Gabor 滤波器系数。
在图像处理中,以Dennis Gabor命名的Gabor 滤波器是一种用于纹理分析的线性滤波器,本质上是指它分析图像中在点或区域周围的局部区域内特定方向上是否存在特定频率成分的分析。
Gabor 用于无数图像处理应用中,用于边缘检测、纹理分析、特征提取等。一些哺乳动物的视觉皮层中某些细胞的特征可以通过这些滤波器来近似. 这些滤波器已被证明在空间和频域中都具有最佳定位特性,因此非常适合纹理分割问题。Gabor 滤波器是特殊类别的带通滤波器,即它们允许某个“频带”的频率并拒绝其他频率。Gabor 滤波器可以看作是由高斯波调制的特定频率和方向的正弦信号.
下图显示了一种这样的 2D Gabor 滤波器。
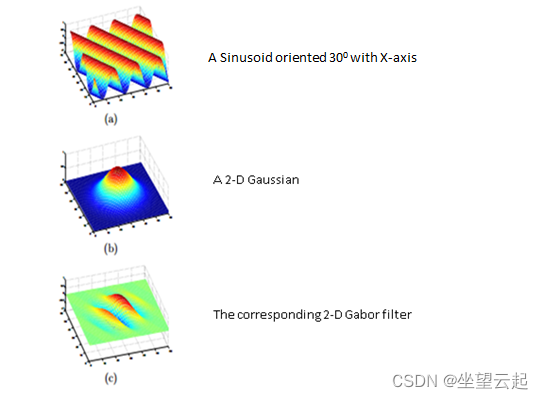
从上图中,我们可以注意到正弦曲线已在空间上定位。在实际分析纹理或从图像中获取特征时,使用了一组具有不同方向的 Gabor 滤波器。
2、可视化
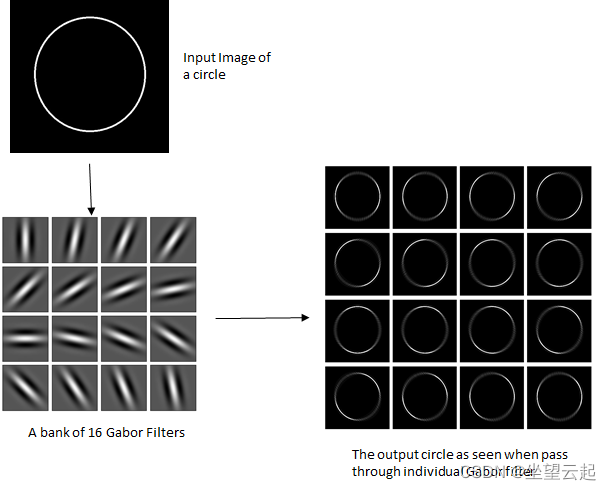
考虑一个大象的例子,它的皮肤上有不同方向的图案或条纹。现在为了突出或提取所有这些模式,我们将在 11.25度 的方向上使用一组 16 个 Gabor 滤波器(即,如果第一个滤波器位于 0度,那么第二个将位于 11.25度,第三个将位于 22.5度,以此类推。)。下图显示了 16 个滤波器的所有滤波器组

当输入图像与所有 Gabor 滤波器进行卷积时,模式很容易突出显示,如下图所示。当将 Gabor 滤波器应用于图像时,它在边缘和纹理变化的点处给出最高响应。当我们说过滤器对特定特征做出响应时,我们的意思是过滤器在该特征的空间位置上具有区分值。

为了更好地理解每个过滤器在输入图像中检测到的内容,请考虑在黑色背景中使用一个简单的白色圆圈。当该图像通过滤波器组中的每个滤波器时,被检测到的圆的边缘是以 Gabor 滤波器所定向的角度定向的边缘。下图清楚地表明了这一点。
3、参数的作用
有一些参数可以控制 Gabor 过滤器的方式以及它将响应哪些功能。2D Gabor 滤波器可以看作是由高斯波调制的特定频率和方向的正弦信号。该滤波器具有表示正交方向的实部和虚部。这两种成分可以形成复数或单独使用。方程如下所示:
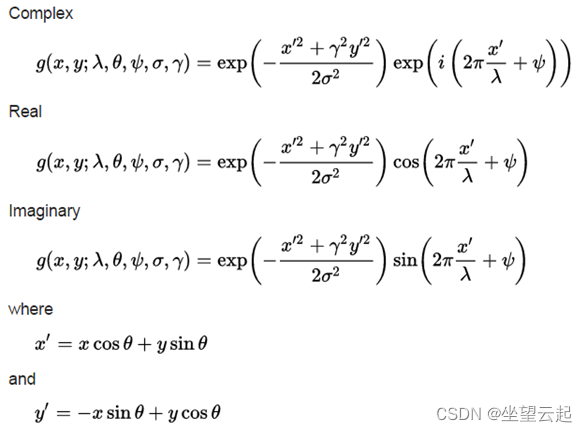
在上述等式中,
λ - 正弦分量的波长。
Ө — Gabor 函数的平行条纹的法线方向。
Ψ -正弦函数的相位偏移。
σ - 高斯包络的 sigma/标准差
ɣ — 空间纵横比,指定 Gabor 函数支持的椭圆度。
上面提到的五个参数控制着 Gabor 函数的形状和大小。下面详细讨论每个参数的作用。为了说明参数的影响,选择以下值作为起点:
λ (λ) = 30;θ ( Ө) = 00;伽玛 (ɣ) = 0.25;西格玛 (σ) = 10;psi ( Ψ ) = 0
(1)拉姆达 (λ):
波长决定了 Gabor 函数条带的宽度。增加波长会产生较粗的条纹,而降低波长会产生较细的条纹。保持其他参数不变并将 lambda 更改为 60 和 100,条纹变得更粗。

(2)θ ( Ө ):
theta 控制 Gabor 函数的方向。零度 theta 对应于 Gabor 函数的垂直位置。

(3)伽玛 (ɣ):
纵横比或伽玛控制 Gabor 函数的高度。对于非常高的纵横比,高度变得非常小,对于非常小的伽马值,高度变得非常大。在将 gamma 值增加到 0.5 和 0.75 时,保持其他参数不变,Gabor 函数的高度减小。

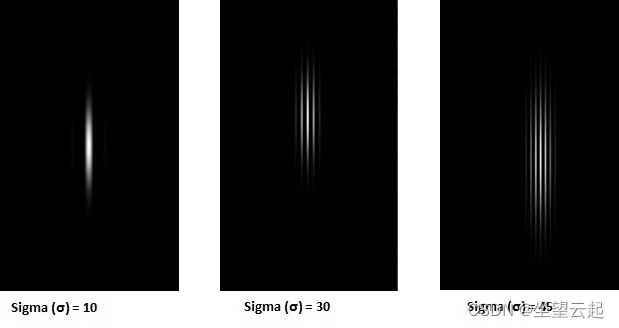
(4)西格玛 (σ):
带宽或 sigma 控制 Gabor 包络的整体大小。对于更大的带宽,包络增加允许更多的条带,而对于小带宽,包络会收紧。将 sigma 增加到 30 和 45 时,Gabor 函数中的条纹数会增加。
二、getGaborKernel函数
1、函数原型
cv::getGaborKernel (Size ksize, double sigma, double theta, double lambd, double gamma, double psi=CV_PI *0.5, int ktype=CV_64F)2、参数详解
| ksize | 返回的过滤器大小。 |
| sigma | gaussian envelope的标准差 |
| theta | Gabor 函数的平行条纹的法线方向。 |
| lambd | 正弦因子的波长。 |
| gamma | 空间纵横比。 |
| psi | 相位偏移。 |
| ktype | 滤波器系数的类型。 它可以是 CV_32F 或 CV_64F 。 |
三、OpenCV源码
1、源码路径
opencv\modules\imgproc\src\gabor.cpp2、源码代码
cv::Mat cv::getGaborKernel( Size ksize, double sigma, double theta,
double lambd, double gamma, double psi, int ktype )
{
double sigma_x = sigma;
double sigma_y = sigma/gamma;
int nstds = 3;
int xmin, xmax, ymin, ymax;
double c = cos(theta), s = sin(theta);
if( ksize.width > 0 )
xmax = ksize.width/2;
else
xmax = cvRound(std::max(fabs(nstds*sigma_x*c), fabs(nstds*sigma_y*s)));
if( ksize.height > 0 )
ymax = ksize.height/2;
else
ymax = cvRound(std::max(fabs(nstds*sigma_x*s), fabs(nstds*sigma_y*c)));
xmin = -xmax;
ymin = -ymax;
CV_Assert( ktype == CV_32F || ktype == CV_64F );
Mat kernel(ymax - ymin + 1, xmax - xmin + 1, ktype);
double scale = 1;
double ex = -0.5/(sigma_x*sigma_x);
double ey = -0.5/(sigma_y*sigma_y);
double cscale = CV_PI*2/lambd;
for( int y = ymin; y <= ymax; y++ )
for( int x = xmin; x <= xmax; x++ )
{
double xr = x*c + y*s;
double yr = -x*s + y*c;
double v = scale*std::exp(ex*xr*xr + ey*yr*yr)*cos(cscale*xr + psi);
if( ktype == CV_32F )
kernel.at<float>(ymax - y, xmax - x) = (float)v;
else
kernel.at<double>(ymax - y, xmax - x) = v;
}
return kernel;
}