MATLAB强化学习入门——二、网格迷宫、Q-learning算法、Sarsa算法

一、多步决策问题和网格迷宫

上一篇文章里讨论多臂赌机问题是单步最优决策问题的对应模型。而在这之后，则可以考虑离散的多步决策问题。离散的多步决策问题，对应的典型问题模型则是网格迷宫(Grid World)。
前文中，ε-greedy策略，softmax策略的原理及其特点得到了讨论。而这些策略，可以看作智能体应对某一状态时选择动作的方式。策略应用的前提，则是智能体对于动作的优劣有着某种估计（无论正确与否）。
当策略应用到多步决策问题上时，如果想要令同样的策略产生作用并选择动作，就需要对系统所处的每一个状态以及对应动作的优劣进行估计。状态价值函数 V(x) (state value function)以及状态-动作价值函数Q(x,a) (state-action value function)也就应运而生了。

图1 Windy Grid World

网格迷宫问题可以描述为智能主体在一个类似棋盘的离散网格空间中学习到达目标点的最优策略的问题。在普通的网格中增加一些变化，添加影响小球运动的风速，即得到Windy Grid World，如图一。智能体在该情况下的移动，受到时不变的风速影响。
状态价值函数与动作-状态价值函数之间的关系可以用Bellman方程得到，具体可参看[1]或者浙江大学的机器学习MOOC。而在算法的具体实现上，往往仅仅需要动作-状态价值函数，即Q函数。
总的思路是，智能体先产生对动作-状态价值函数空间的初始估计。在尝试的过程中，根据尝试所得到的结果对Q函数进行迭代；直至得到能够促使智能体做出最优选择的Q函数。
这样的迭代可以采取不同的周期(episode)进行。当智能体每走完一次迷宫后（走到目标、走出边界、超出限定步数）对Q函数进行迭代，为蒙特卡洛方法。当智能体每走一步即对Q函数进行迭代，为时序差分(Time Difference)方法。同样，也可以依据不同的值和计算方式对Q函数进行迭代。具体而言，则主要有Q-learning算法，Sarsa算法，以及Sarsa-λ算法。

二、 Windy Grid World的编程实现

想要对上述算法进行对比讨论，需要设置一个统一的网格迷宫。网格迷宫的大小为10×7。智能体的起点坐标为(1,4)，目标点坐标为(8,6)，在横坐标x∈[4,9]的区域内存在+y向大小为1的风速，即智能体在有风区域运动时每运动1步会在风的作用下向上运动1格。网格迷宫的设置可以用图一展示。
智能体存在4种运动方式：向右(+x)、向左(-x)、向上(+y)、向下(-y)移动1格。因此智能体的Q函数是一个10×7×4的三维矩阵。设置智能体到达目标的奖励(reward)为+5，若智能体超出边界，奖励为-1。

三、 Q-Learning算法

Q-learning算法是一种单步迭代算法。它的具体迭代方式是：首先利用某种策略选择系统在当前状态的动作，并得到下一状态；利用下一状态的奖励和最优动作值函数对本动作值函数进行迭代。
其具体算法如图2：

图2 Q-Learning算法

由于其用于迭代的次动作a’为次状态s’下Q函数最大的动作，并不一定与策略π在次状态下选择的动作相一致，因此Q-learning算法是一种离策略(off-policy)的算法。

3.1 算法的实现

1. 在智能体的动作策略上，选择策略π为时变ε-greedy策略。
2. Q函数的迭代
   在Q函数迭代的具体实现中，智能体Q函数中每个状态的初值设置为(0.2,0,0,0)。
   除去图2中展示的迭代方式，还需考虑一些特殊情况。当智能体的下一状态若在边界之外或到达目标，此时的Q(s’,a’ )=0。
3. 成功与失败的判断
   将当智能体在40步内到达目标，视作成功，若智能体走出边界，或者在40步之内未能达到目标点，则视为失败。
4. 部分功能的封装
   与多臂赌机类似，将部分功能封装，这其中包括智能体选择动作的ε-greedy策略，函数名tcegreedy；智能体在风的影响下运动，函数名movement；

总的学习循环设置为6000次，学习率alpha=0.5；传递衰减率gamma=0.99。代码如下：

%I thought what I'd do was I'd pretend I was one of those deaf-mutes, or should I?

clear all;

%风速初始化
Windyworld.windx=zeros(7,10);
Windyworld.windy=zeros(7,10);
Windyworld.windy(:,4:9)=Windyworld.windy(:,4:9)+1;

targetxy=[6,8];                 %!!注意：第一个坐标为y坐标，第二个坐标为x坐标


alpha=0.5;
gamma=0.99;                     
Tloop=6000;                       %总学习循环次数
mark=zeros(1,Tloop);             %记录是否成功

%迭代为二重时间循环
Q_func=zeros(7,10,4);            %!!三维值函数矩阵：（z=1：+x）（z=2：-x）（z=3：+y）（z=4：-y）
Q_func(:,:,2)=0.2;               %size(B),ndims(B)
Q_func(targetxy(1),targetxy(2),:)=0;     %目标值的所有Q函数始终为0
    
for Ts=1:Tloop                   %Ts=study time
    %单次运动初始化
    rolexy=[4,1];
    result(Ts).Q_func=zeros(7,10,4);
    result(Ts).trace=zeros(40,3);
    result(Ts).trace(1,:)=([1,rolexy(1),rolexy(2)]);
    for Tm=1:40
    %按照策略获得到达下一步的动作
        act=tcegreedy(Ts,Q_func(rolexy(1),rolexy(2),:));
        nextxy=movement(act,rolexy,Windyworld);
    %TD算法进行策略值迭代
        %计算reward
        if nextxy(1)==targetxy(1)&&nextxy(2)==targetxy(2)  %到达目标
            reward=5;
        else if nextxy(1)<1||nextxy(1)>7||nextxy(2)<1||nextxy(2)>10 %超出边界
                reward=-1;
            else
                reward=0;
            end                     %reward不考虑超出步数的问题
        end
        %计算下一步的策略函数最大值
        %Qlearning方式进行Q函数更新，更新Q值中所用的s'状态下动作与实际在s'状态下做出动作不一定相同（因为e-greedy的存在）
        if nextxy(1)<1||nextxy(1)>7||nextxy(2)<1||nextxy(2)>10 %超出边界
            Q1=0;
        else
            Q1=max(Q_func(nextxy(1),nextxy(2),:));
        end
        Q_func(rolexy(1),rolexy(2),act)=(1-alpha)*Q_func(rolexy(1),rolexy(2),act)+alpha*(reward+gamma*Q1);
    %更新坐标
        rolexy=nextxy;
        result(Ts).trace(Tm+1,:)=([Tm+1,rolexy(1),rolexy(2)]);
    %判断是否跳出本episode
        if rolexy(1)==targetxy(1)&&rolexy(2)==targetxy(2)
            mark(Ts)=1;
            break;
        else if rolexy(1)<1||rolexy(1)>7||rolexy(2)<1||rolexy(2)>10
                break;
            end
        end        
    end
    result(Ts).Q_func=Q_func;
end

Avegain=zeros(1,Tloop);
for i=1:Tloop
    Avegain(i)=sum(mark(1:i))/i;
end

3.2 结果的讨论

选取两个参数不同的ε-greedy策略进行实验，智能体的平均成功率随尝试次数变化的规律如下：
除去策略π会影响智能体的平均成功率外，Q函数的初值亦显著影响Q函数的初值，如下图：

四、Sarsa算法

Sarsa算法全称为State-Action-Reward-State-Action。它与Q-learning算法的主要区别在Q函数的迭代上。作为一种在策略(on-policy)的算法，它运用次状态下智能体根据策略选择的动作价值函数对当前状态的Q函数进行更新，如下图：

与Q-learning算法相比，Sarsa算法能有效改善初值的影响，如图11所示：

五、Sarsa-λ算法

Q-learning算法与Sarsa算法均是单步迭代算法。而若想要更好的利用长期回报带来的影响，让最终的奖赏更快速的传播到起始点，就出现了多步迭代的Sarsa-λ算法。这其中的λ就是控制影响迭代的历史轨迹长度的参数。当λ=0时，即为单步迭代的Sarsa算法；当λ=1时，即为全周期迭代的蒙特卡洛方法。
具体的实践上，则利用了一个记录历史轨迹和轨迹衰减情况的E矩阵，如下图：
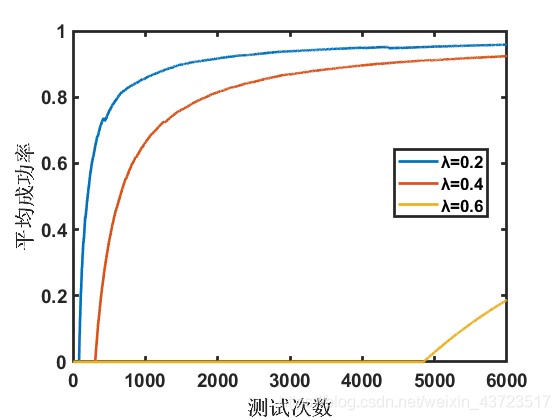
取不同的λ值，得到如下图所示的结果：
图示结果表示，λ取合适的值时，可以有效的提高学习的效率，如图中λ=0.65及λ=0.8的曲线。当λ趋近于1时，学习的效率反而下降了。在这种情况下，每完成一个运动周期才会对Q函数进行整体更新，而全部的可能情况有4^40种，显然这样的更新速率是不够的。而由于传递距离较远的原因，一条错误的轨迹可能在较长的时间内对Q函数产生影响，因此而出现了λ=0.99曲线种长时间成功率下降的情况。
另一方面，λ的取值对初值的敏感性是不同的，λ越大，敏感性越高，取Q_i=(0,0.2,0,0)，结果如下：

总结

以上，就实现了几种主要的解决离散多步决策问题的算法。无论哪一种算法，都需要一个记录每一个状态-动作对对应价值函数的矩阵。这样一个矩阵将随着解决问题复杂程度而明显增加。上述例子中，Q函数矩阵的维数是10×7×4的。如果问题复杂一些，智能体一次可以走一步，也可以走两步；迷宫的边长也增加至100个，那么Q函数矩阵就骤增至100×100×4维。如果决策问题是连续的，上述算法更是没有办法解决。
面对连续决策问题，神经网络的作用就发挥出来了。神经网络能够拟合Q函数在特征空间中的趋势，从而实现对连续决策的控制。这就是Deep Q-Learning: 深度Q学习。

[1] 周志华. 机器学习[M]. 北京：清华大学出版社, 2016.