梯度与梯度下降法
1 前言
机器学习中的大部分问题都是优化的问题,而绝大部分问题都可以使用梯度下降法处理,那么搞懂什么是梯度,什么是梯度下降法就非常重要了,这是基础中的基础,也是必须掌握的概念.
2 导数
一张图读懂导数与微分
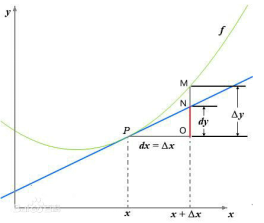
导数定义如下:
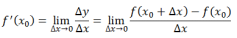
反映的是函数y=f(x)在某一点沿着x轴的正方向的变化率/变化趋势.直观地看,也就是在x轴上某一点处,如果f(x)>0,说明f(x)的函数值在x点沿着x轴(方向)正方向是趋于增加的,相应的f(x)<0,说明函数f(x)的值在x点沿着x轴(方向)正反向趋于减少.
3 导数与偏导数
偏导数的定义如下:
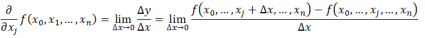
导数与偏导数的本质一致,都是当自变量的变化量趋于0时,函数值的变化量与自变量比值的极限,直观地说,偏导数也就是函数在某个点沿着坐标轴(xi方向)正方向的变化率(如上面公式是沿着xj轴(方向)的变化率).同时如果一个函数有多个自变量(xi)时,某个点是有多个方向所对应的偏导数的.
4 导数与方向导数
方向导数的定义如下:
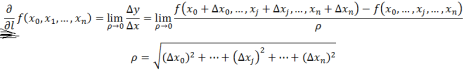
在前面导数与偏导数的定义中,均是沿着坐标轴正方向讨论函数的变化率,那么当我们讨论函数沿任意方向的变化率时,也就引出了方向导数的定义,即某一点在某个趋近方向上的导数值.
通俗的解释:
我们不仅要知道函数在坐标轴正方向上的变化率(即偏导数),而且还需要知道设法求得函数在其他特定方向上的变化率,而方向导数就是函数在其他特定方向上的变化率.
特定方向:方向导数中画黑线的就是一个方向,上图定义的就是函数某点在l方向的方向导数.而
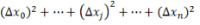
就是这个点沿着l方向,分别在x0轴,x1轴…xn轴方向的增量.
5导数与梯度
梯度的定义如下:
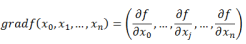
梯度的提出只为回答一个问题:
函数在变量空间的某一点处,沿着哪一方向有最大的变化率?
梯度的定义如下:
函数在某一点的梯度是这样一个向量,它的方向与其取得最大方向导数的方向一致,而它的模为这个点方向导数的最大值.
这里注意三个点:
梯度是一个向量,即有方向有大小
梯度的方向是最大方向导数的方向
梯度的值是最大方向导数的值
知道了函数在这个点的梯度,就相当于知道函数在这个点方向导数最大值的方向,沿着这个方向的负方向最大化的减小函数.梯度下降法就是用的这个原理.
6 导数与向量
提问:导数,偏导数,方向导数是向量么?
向量的定义是有方向,有大小的量
从前面的定义可以这样看出,偏导数与方向导数描述是函数在某一点沿着某个方向的变化率,也就是具有方向和大小的.因此从这个角度来理解,我们可以把偏导数与方向导数看成一个向量,向量的方向就是变化率的方向,向量的模,就是变化率的大小
沿着这一思路来理解梯度:
梯度即函数在某一点最大的方向导数,函数沿着梯度方向函数有最大的变化率
7 梯度下降法
既然在变量空间的某一点处,函数沿梯度方向有最大的变化率,那么在优化目标函数的时候,自然是沿着负梯度方向去减小函数值,以此达到我们的优化目的.
如何沿着负梯度方向减小函数值呢?
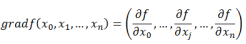
同时梯度与偏导数都是向量,那么参考向量运算法则,我们在每个变量轴上减小对应变量值即可,梯度下降法可以描述如下:
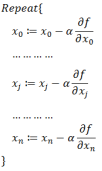
对这里的理解:
此时函数f(x)在某一点处确定它的梯度,此时函数如果沿着梯度方向的负方向下降,学习步长为α(通常为0.1或0.01),函数值的下降是最快的.而右边α与各轴偏导数的乘积可以看做f(x)沿着梯度负方向下降时,对应各轴的增量(增量导致x0…xn的变化必然会导致损失函数取值的减小).当下降到另一点时,需要重新计算当前点的梯度与再次迭代此函数值的变化,所以需要一个repeat的过程.从而找到函数f(x)的最小值.
取函数在某一点的负梯度方向来降低函数值:如图所示
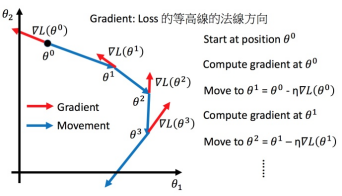
8 梯度下降法与机器学习
上文提到的函数就可以理解为机器学习中的损失函数/目标函数.自变量x1,x2…xn就可以理解为损失函数中需要优化的参数,通过不断的优化参数(更新x1,x2…xn),找到损失函数最小的那个点.
自变量xi有时候与特征相对应,有时候与别的对应,具体要看损失函数是怎么定义的.
9 梯度下降法的缺点
1 靠近极小值时收敛速度减慢
2 直线搜索时可能会产生一些问题
3 可能会”之字形”地下降
10 补充:向量函数求导的问题
首先,向量求导只是矩阵求导的一个特例而已.
10.1对标量求导
1.向量对标量求导,结果是个向量
事实上就是向量的每一个元素对标量求导,举个例子对于y(x)=(y1,…,yn),其中x是个标量:
2.矩阵对标量求导,结果是个矩阵
事实上也就是矩阵的每一个元素对标量求导.对于矩阵Y(x)=(yij):
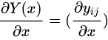
10.2对向量求导
1.标量对向量求导,结果是向量
事实上这就是所谓的Gradient,即对于一般标量函数f(x),其中x=(x1,…,xn):
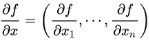,有时候也记为▽f
以上的向量同时指代行向量与列向量
2.向量对向量求导,结果是矩阵
行向量对列向量求导:
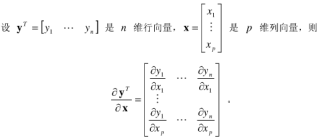
列向量对行向量求导:
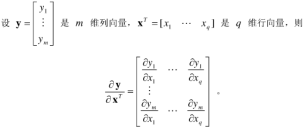
行向量对行向量求导:
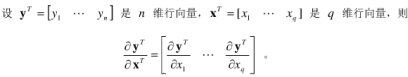
所以结果向量中的每一个元素都是一个向量对标签求导
列向量对列向量求导:
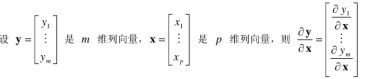
相当于结果向量中的每一个元素都是一个梯度.
3.矩阵对向量求导,结果是个三维object,先来个gradient,然后其中每个元素都是个matrix.