【信号与系统学习笔记】—— 连续时间信号的离散时间处理

在此之前，我想重新回顾一下理想采样的频谱特征，同样地，先看看框图：

这里是两个时间信号在时域上的相乘运算。根据傅里叶变换的特性： $x(t)s(t) \space \underleftrightarrow{\mathscr{F}} \space \frac{1}{2π}\int_{-∞}^{+∞}X(jθ)S(j(ω - θ))dθ$
而我们知道， $S(ω)$ 是一系列周期为 $T_s$，幅度是 $\frac{2π}{T_s}$ 的冲激串。跟外面的系数 $\frac{1}{2π}$ 相乘，我们可以知道：

经过理想采样之后的信号的频谱，就是首先原信号 $x(t)$ 的频谱幅度变成了 $\frac{1}{T_s}$，然后再以 $ω_s$ 做周期延拓所得到的。 如下图示所示：

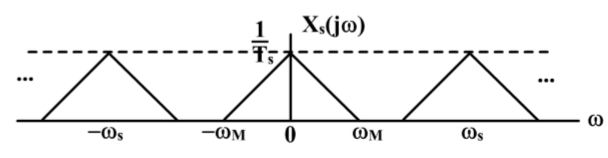
OK！这就是上一次博客的内容。下面我们进入正题—— “连续时间信号的离散时间处理”。这名字这么绕口，为什么要这样做呢？

首先，在很多应用里面，我们都是先把连续时间信号转化为离散时间信号，对这个离散时间信号做处理，然后再把离散时间信号转回连续时间信号。这样做有一个显著的好处：我们的计算机非常善于处理离散信号。

下面我们直接先来看看这个过程的框图：

我们学习这一部分的要求就是能够熟练地画出上图所示的各种信号的频谱。下面我们来看看：

Part1 包括两个部分 —— 理想采样 + 冲激串到序列（这两个部分构成的就是我们所说的 C/D 转换，也叫 A/D 转换）即连续时间信号转离散时间信号。我们先从时域分析一下：

这是 $x_c(t)$ 的波形：

那么我们就可以画出 $x_s(t)$ 的波形：

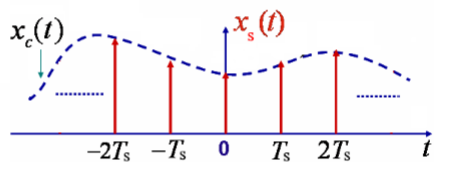
到这里有些读者可能就会纳闷了 —— 你这经过采样之后不就已经是离散信号了吗，那为什么还要加上 “ 冲激串到序列”这一步呢？其实大家注意：虽然看起来已经是离散的形式了，可是我们的横轴还是 “t" ！我们需要转为 “n” ，才是真正完成了离散化的步骤。

因为对于离散信号而言，n 都要死整数，所以我们希望得到下面的离散时间信号：

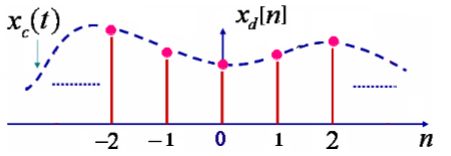
那么，我们就会发现：只要对 $x_s(t)$ 的横轴都除以 $T_s$ ，就可以得到这个 $x_d[n]$ 了！这就完成了离散化处理。

下面我们从频域分析一下：根据对偶性给我们带来的启发——如果在时域上做除以 $T_s$ 的处理，那么在频域上就需要做 乘以 $T_s$ 的处理！

首先， $x_c(t)$ 的频谱大家已经非常熟悉了：

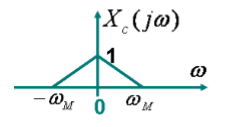
经过理想采样得到的频谱就是：

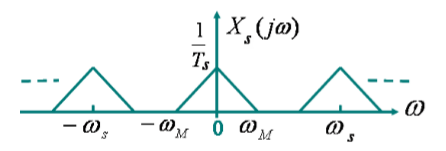
如果我们设离散时间信号的频谱的横坐标用 $Ω$ 表示，那么可以得到：

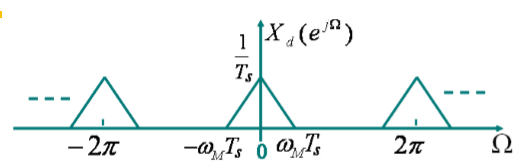
$ω_s$ 乘上 $T_s$ 就会得到 $2π$

我们把时频放在一起对比：

我们得到了一个重要结论：对于连续时间下的冲激串要转换为离散时间的序列

1. 时域上有： $n = \frac{t}{T_s}$
2. 频域上有： $Ω = ωT_s$

---

有了 C/D的基础，D/C 也不在话下了：D/C 过程中，我们同样是遵循上面两条公式的。