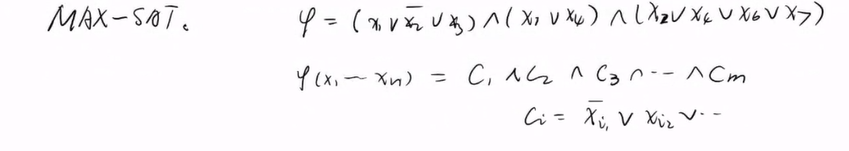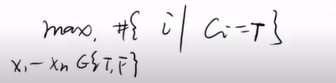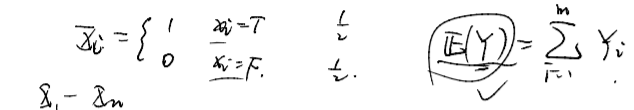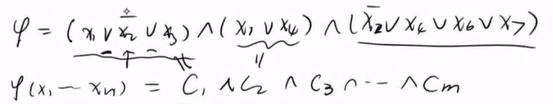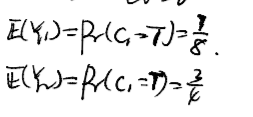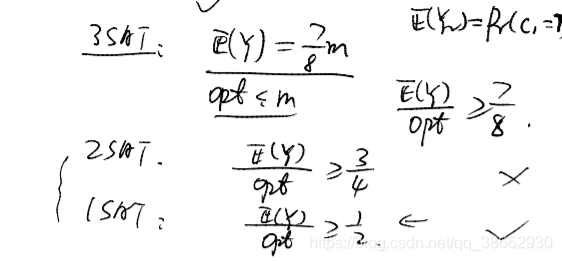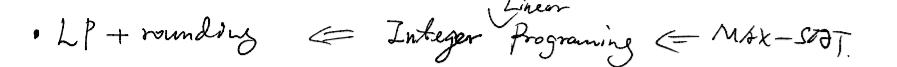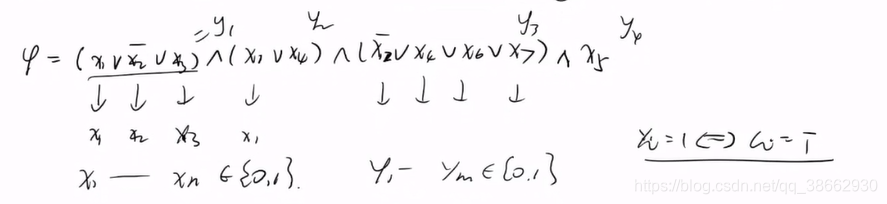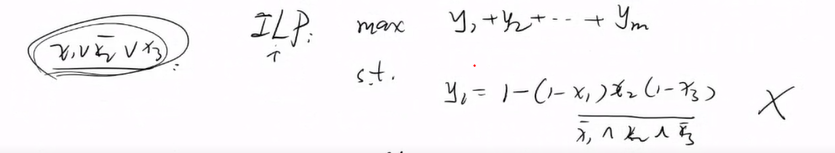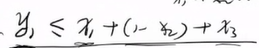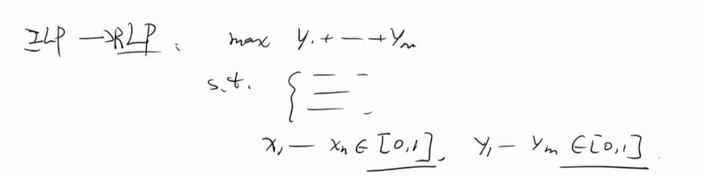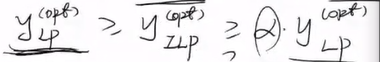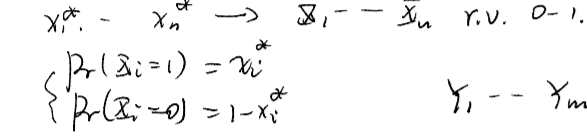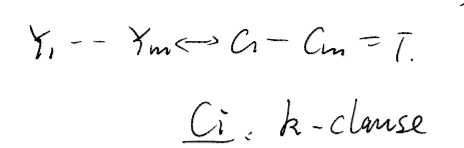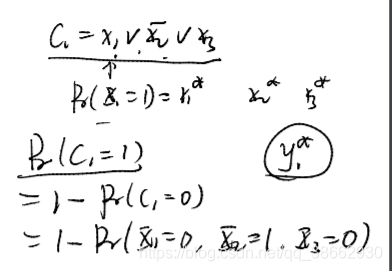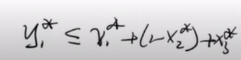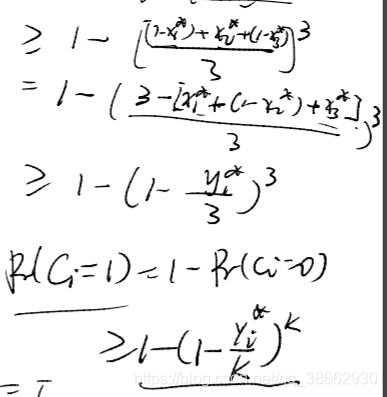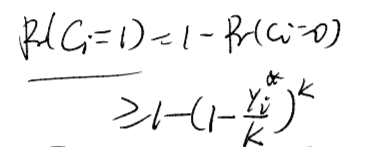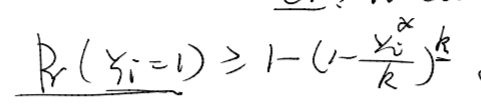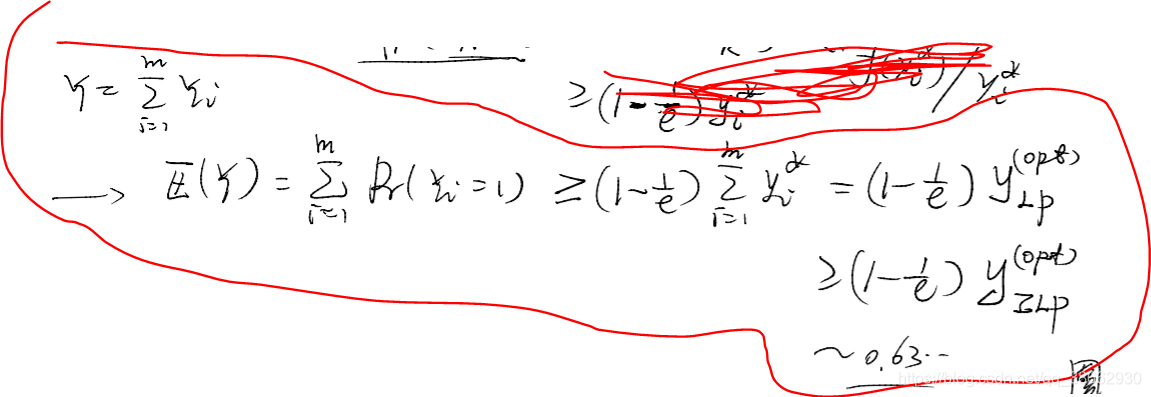高级算法设计分析-- Max-SAT（随机算法>近似算法）

笔记来源：高级算法设计（孙晓明老师部分）
https://en.wikipedia.org/wiki/Maximum_satisfiability_problem#Weighted_MAX-SAT
随机算法在近似算法中的应用
本节问题可能利用条件期望去随机化，将随机化算法转化为近似算法，也可以利用LP+rounding+ 条件期望去随机化

1. MAX-SAT定义

SAT，NP问题是否存在一系列变量的取值为真或假使得给定句子为真，SAT不身是不可判定的问题。

MAX-SAT，输入是一系列析取表达式，存在n个变量，m个子句，每一个子句合取表达式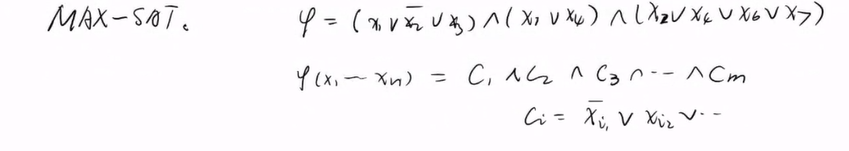
输出是最大化可以取真的子句的数量，n个变量可以为真，也可以为负。

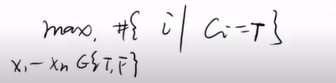
2. MAX-SAT 求解

希望作一个近似算法，求出的值 $A$尽可能的接近最优的最大值 $OPT$,使其比值 $A/opt$尽可能为1。

2.1 条件期望去随机化近似算法

先设计一个不太差的随机算法，然后再去随机化 ：设计0-1变量 $X_i$,将 $X_1,\dots,X_n$随机赋值。，求出期望能满足的子句个数 $E(Y）$

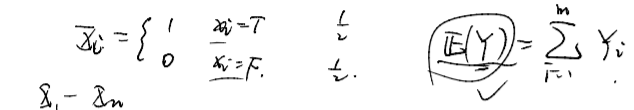
$Y_i对应子句C_i,如果子句C_i为真，则Ｙ_i=1$

例如表达式

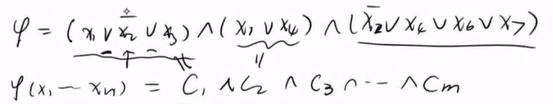
而每个子句期望或者说为真的概率与子句中变量有关，变量个数越多，则对应的概率越高。

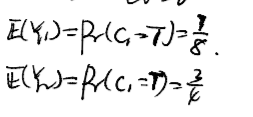
因此对于3SATR,，则对应的E(Y)/opt可以达到一个7/8的近似。

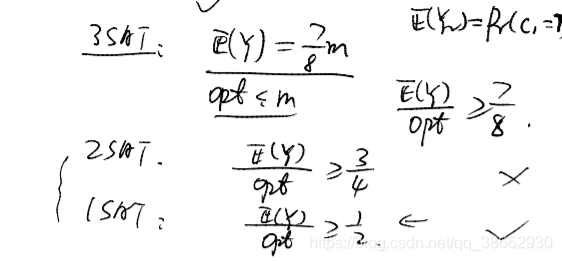
对于混合的SAT通过不同的权重都可以获得一个比较高的E(Y)
接下来可以通过去随机化获得一个较好的近似算法

2.2 接下来考虑另外一种算法LP+rounding

思路转化：

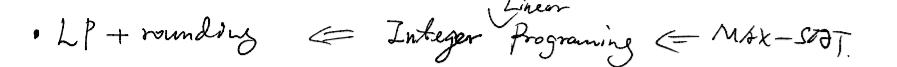
2.2.1 MAX-SAT转化为ILP。

MAX-SAT 转化为ILP，两者是等价的，即整数线性规划的解 $y_{ILP}^{opt}$是精确解，这里没有采用近似，但是不易求解，因此松弛为线性规划 ，线性规划的解是近似的，且有 $y_{LP}^{opt}>y_{ILP}^{opt}$

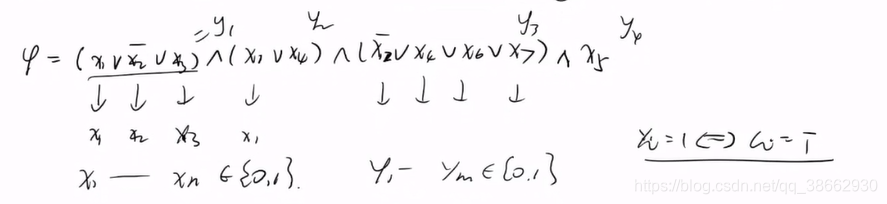
将不同的变量用 $X_1\dots,X_n$表示，不同的子句对应一个变量 $y_i\{i=1,2,\dots,m\}$
如何将每一个子句用变量形式化表达？（1）代数化方法

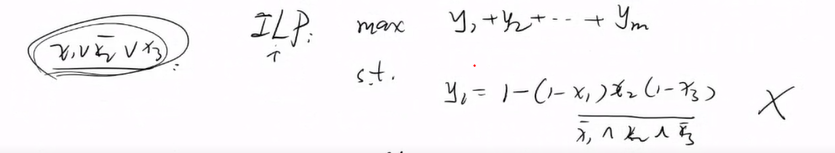
若将 $y_1$表示成这样的方式，约束条件不是线性规划了。
只要析取表达式中变量只要有一个是1 就是1，当所有变量为0 时，y为零，因此与以下等价


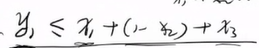
这就是如何将MAX-SAT 转化为等价的整数线性规划，

2.2.2 ILP转化为RLP。

将整数线性规划松弛为线性规划

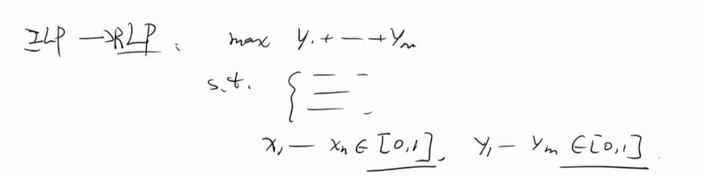
椭球法和内敛法可以多项式时间复杂度内求解Relaxiation LP
由于松弛后可行域变大因此 $y_{LP}^{opt}>y_{ILP}^{opt}$.我们希望 $y_{LP}^{opt}$能否大于 $\alpha y_{LP}^{opt}$,这样的话可以得到一个 $\alpha$近似（比值）

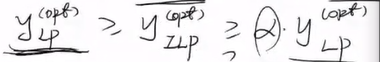
2.3 ·LP->LP+Rounding

用 $x_1^*,\dots,x_n^*,y_1^*,\dots,y_n^*,$表示松弛后的LP的解 $y_{LP}$，然后利用Rounding （随机舍入）方法由 $x_1^*,\dots,x_n^*,y_1^*,\dots,y_n^*,$出发得到一个最终的近似解 $x_1,\dots,x_n,y_1,\dots,y_n$,且有 $y\ge?y_{ILP}{opt}$

接下来求Rounding 后的解：设独立的随机变量 $X_i$,表示子句 $C_i$中的合取变量
目前已经求出了LP的解 $x_1^*,\dots,x_n^*$由于其属于0-1 之间，因此可以将其看作是 $X_i$取不同值的概率值，那么 $X_i$最终确定下来的值作为最后的解。具体来说，

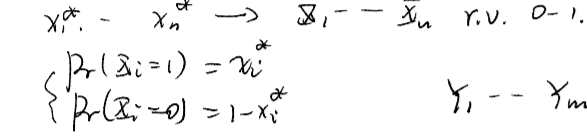
将不同的子句用取值0-1 之间的随机变量表示，即每一个子句的取值都有0-1

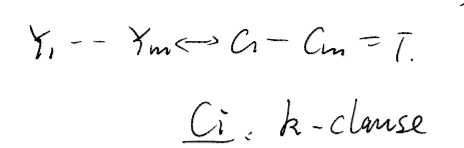
那么 $Y=\sum Y_i$即为rounding 后的最终的近似解，以下这里求出它的期望的界。

2.3.1 求期望的界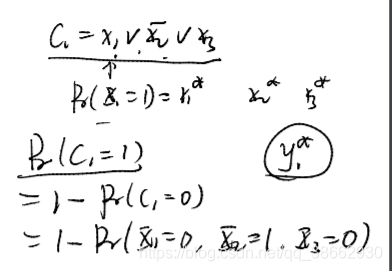

怎样将其和 $y_1^*$联系起来呢，由均值不等式及约束条件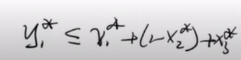

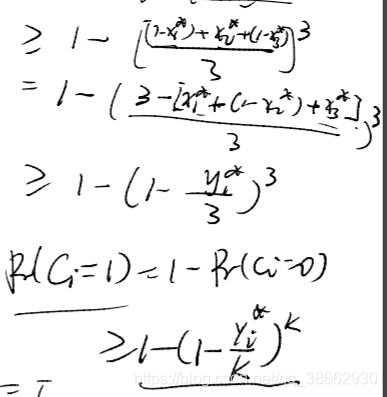
一般的对于有k个变量的 $C_i$子句有下列式子成立

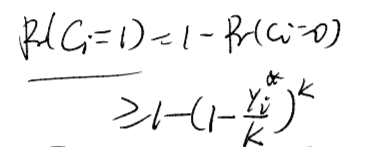
即我们将每一个 $y_i$与 $y_i^*$联系起来了

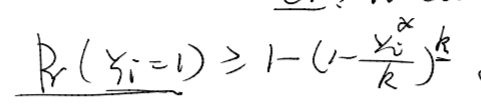
它是关于 $y_i^*$为变量的函数，其中这里的k是常数

可以令 $1-(1-\frac{y_i^*}{k})^k=f(y_i^*)$
$\frac{f(y_i^*)}{y_i*}$求导，当 $y_i^*=1$有极小值，并利用放缩求得
$f(y_i^*)\ge(1-(1-\frac{1}{k})^k)*y_i^*\ge(1-\frac{1}{e})*y_i^*$

之所以变成这样的形式，是为了求出先前提到的 $\alpha$

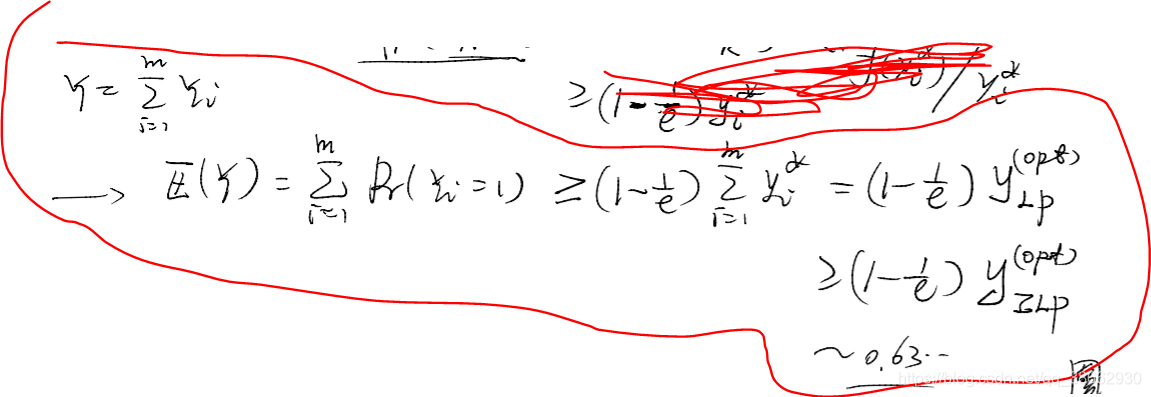
即做到0.63的近似，(LP是松弛后的结果，实际中比它大，因此这个界只会大于0.63)
在实际中当每个 $C_i$出现的变量不一致时，实际中，对于每个 $X_i$根据其出现次数作为权重进行概率赋值，而不是1/2，比如X_i 的补出现的次数比X_i出现的多，则 $P{X_i=1}<\frac{1}{2}$

上面近似算法利用LP+ rounding (随机舍入)求得一个不低于0.63的期望值，

因此可以通过条件期望去随机化，
求得一个 $Y=f(x_1,x_2,\dots,x_n)\ge E(Y)\ge0.63opt$
这里用到了条件期望去随机化算法的原理，可以参考之前的介绍

主要思路：还是逐个固定不同的变量，然后放缩

$0.63opt \leq E(Y)=Pr(X_1=1)E(Y|X_1=1)+Pr(X_1=0)E(Y|X_1=0)=x_1^*\phi_{1,1}+(1-x_1^*)\phi_{1,0} \le \max(\phi_{1,1},\phi_{1,0})<\dots<\dots<E(Y|X_1=x_1,X_2=x_2,\dots,X_n=x_n)=f(x_1,x_2,\dots,x_n),$
其中的 $E(Y|X_1=x_1,X_2=x_2,\dots,X_i=x_i,X_{i+1},\dots,X_{n})的下界求法用上面的Rounding ,即类似于E(Y)下界 的求解$