一、优化问题(Optimization Problem)
一个优化问题要么是最小化问题要么是最大化问题,其主要由以下三个部分组成:
1)一个问题实例集; 2)求出所有实例的所有解作为候选解; 3)对候选解进行检测的方法;
在候选解中最小(最大)的称为最小解(最大解)
二、近似算法(Approximation algorithm)
绝对近似算法(absolute algorithm):如果一个算法对优化问题A的所有实例都有解,并且该算法对实例产生的解决方案
A(I)和最优方案OPT(I)对所有实例都满足|A(I)-OPT(I)|<=K,则为绝对近似算法;
相对近似算法(relative algorithm):如果一个算法对优化问题A的所有实例都有解,并且该算法对实例产生的解决方案
A(I)和最优方案OPT(I)对所有实例都满足A(I)/OPT(I)<=K,则为相对最小化算法;OPT(I)/A(I)<=K,则为相对最大化算法;
三、几种相对近似算法的证明(2-VC,2-Bin Pack,1.5-Metric TSP)
1)VC问题的相对近似算法,证明A(I)/OPT(I)<=2;
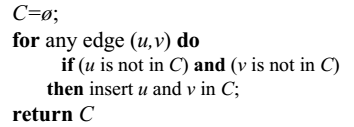
对于一个图G=(V,E),根据上述算法加入集合C中点所对应的边之间是相互独立的;
在这里A(I)=|C|,OPT(I)>=|C|/2;联立上述两个式子得证A(I)/OPT(I)<=2;
用这个算法求解出来的点的个数为|C|个,构造的这些边之间是相互独立的,要想覆盖这些边最优解OPT(I)所确定的
点的个数一定是大于等于|C|/2的;
上述算法的时间复杂度为O(|E|),算法的时间复杂度只与边数有关;
2)Bin Pack问题的相对近似算法,证明A(I)/OPT(I)<=2;

问题描述:将n个不大于1的数放入不大于1的桶中,确定最少的桶的个数为多少?

对于这个算法需要的桶的个数最多为2A个,A是这些数据的和;
两个相邻的桶之和是大于1的(即:U[k]+U[k+1]>1),在感官上每一个桶的容纳量是大于1/2的,A(I)<=2|A|;
最优解OPT(I)所需要的桶的个数一定是>=|A|的(最优情况每个数都是1,就需要A个桶,但实际一定大于它);
联立上述两个式子得OPT(I)>=A(I)/2,由此得证A(I)/OPT(I)<=2;
上述算法的时间复杂度为O(n),算法的时间复杂度与输入数据的个数有关;
3)Metric TSP问题,证明A(I)/OPT(I)<=3/2;

问题描述:在一个完全图G中,各边满足三角形法则,在图中找出一个哈密顿回路使得花费最小;
1)找出各个图的最小生成树T;时间复杂度为O(eloge)
2)将图中的奇数度的顶点加入到集合Q中;时间复杂度O(n)
3)对这些奇度顶点集计算最优匹配M;时间复杂度O(|Q|^3)
4)将3步骤中新增添的边M加入T中,这样T中的所有点所对应的度数都为偶数,此图为欧拉图,在每次经过
相同的点时都都走最短的路径到达另一个点;时间复杂度O(n)
在新构造的图G中存在一个欧拉回路使得能够遍历所有的边这些边长度和为d(T)+d(M)(欧拉回路长度)
则这个哈密顿回路的路径长度(算法求解的路径)A(I)<=d(T)+d(M);
OPT(I)>=d(T) OPT(I)/2>=d(M)联立上述三个式子得出3OPT(I)/2>=A(I),得出A(I)/OPT(I)<=3/2;
在最优哈密顿回路中删去一条边此图变成了一颗生成树,显然OPT(I)>d(T)成立;
(某一棵生成树的长度一定大于它最小生成树的长度)
四、不可近似算法(Inapproximation algorithm)
问题是不能够通过绝对近似解决或者问题没有恒定的近似比(即不能通过绝对近似和相对近似求解)
五、其他
1)一个问题(程序)包含两部分因素:时间和空间;(如何度量一个算法:问题规模和语句频度)
2)时间(时间复杂度)对于一个算法来说占绝对因素;
一个算法所要考虑的唯一目标就是高效率的解决问题,那么对此就要求算法的执行时间短,而且在运行过程中
所占用的内存低。而空间复杂度一般取决于问题本身(问题规模),与算法无关。算法的时间复杂度追求的是
效率,对于这两种复杂度在通常情况下是对立的,在两者不能统一的时候,往往牺牲空间来追求时间上的高效
率。而且现如今随着计算机的内存容量越来越大,价格也越来越便宜了。
3)高效的算法是能够在多项式复杂程度内解决问题的算法;
