文章目录
前言
本文是对于算法设计的学习笔记，如有错误，请不吝赐教。
在讨论了NP完全性和一般情况下的计算难解性后，我们考虑下面这个问题：对于那些在多项式时间内难以达到目标的问题应该如何设计算法？
在这一节，我们考虑近似算法，它在多项式时间内运行并找到保证接近最优的解。（接近，保证）
我们考虑四个用以设计近似算法的一般技术：
1.贪心算法：找到能产生可证明接近最优解的贪心规则
2.定价法：考虑为了强制服从问题的每一个约束需要付出的成本
3.线性规划：利用线性规划。
4.经过舍入的输入使用动态规划
一、贪心算法和最优值的界限：负载均衡问题
负载均衡问题产生于多服务员需要处理一组工作或者请求的情况。我们认为所有的服务员都一样，每一个都可以服务任何一个请求。
1.1 问题
负载均衡的问题描述如下：给定m台机器M1.。。Mm和n项作业，每一项作业j有处理时间tj，要把每一项作业分配给一台机器使得所有机器的负载尽可能的均衡。
更具体：设有一个作业对机器的分配，令Ai表示分配给机器Mi的作业集，机器Mi需要工作的总时间为
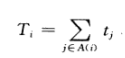
我们把这个称作是机器Mi的负载。
我们要求工期即所有机器的最大负载T=maxiTi最小。
（求这个最小工期分配的调度问题是NP难的）
1.2 算法设计
对这个问题，我们先考虑一个简单的贪心算法，即以任意顺序排序所有的作业，对于每一个作业都将它分配到至今负载最小的机器。
贪心算法：
开始时没有已分配的作业
对于所有的机器Mi，令Ti=0和Ai=0;
for j=1,,,n:
令mj是有最小值Tj的机器
把作业j分配给机器Mj
令A(j)=A(j）+j
令Tj=Tj+tj
endfor
1.3 算法分析
在这里，我们考虑将我们得到的值与最优值T进行比较。
但由于我们无法得到最优解T，所以我们这里考虑最优值的下界。
这里我们考虑m台机器中至少有一台做总工作量的1/m、
或者考虑这样一个下界：
我们需要证明以下结论：
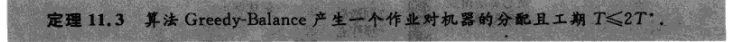
我们考虑当将任务j分配给机器Mi时，此时的Mi时所有机器中负载最小的。其他的机器的负载不小于Ti-tj
所有的相加可得：
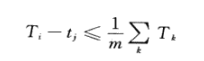
同样我们可以知道Ti-tj<=T*
由此得证。
1.4 一个改进的近似算法
我们现在考虑如何开发一个更好的近似算法。我们需要保证我们的解偏离最优解严格小于2.这里我们考虑上述算法的最坏情况：
即：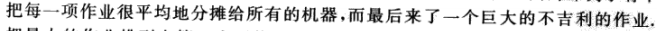
我们改进算法：按照处理时间降序排列，然后其余和之前一样。
我们可以证明改进的算法所得到的分配不超过最优质的1.5倍。
开始时没有已分配的作业
对所有的机器Mi,令Ti=0 和Ai=空
按处理时间tj的递降顺序排列作业
设t1>=t2>=...tn
for j in 1,n:
设机器Mi达到最小值minTk
把作业j分配个机器Mi
令A（i）=A（i）+j
令Ti=ti+tj
endfor
同样考虑负载最大的机器，考虑tj时发配给Mi的最后一项作业，此时tj<=tm+1<=1/2T*
所以得证。
二、中心选址问题
和上一节一样，本节考虑的中心选址问题也与多服务员工作分配有关。中心选址的核心问题是服务员放在什么地方最好。
2.1 问题
中心选址问题：我们有n个地点的集合S，要选择k个中心建设大型购物中心，要选择这k个购物中心的地址成为中心的。
中心成为中心的含义：定义地点s到中心集的距离dist(s,C)=min(dist(s,c)
如果每一个地点距离某一个中心的距离不超过r，那么称C构成一个r-覆盖使得C是r-覆盖最小的r成为C的覆盖半径，我们的目标是选择k个中心的集合C使得rc尽可能的小。
给定整数k，n个地点的集合S以及距离函数。
距离函数满足一下条件：
1.对于所有的s属于S，dist(s,s）=0
2.距离是对称的：对于所有的地点s,z属于S，dist(s,z)=dist(z,s)
3.满足三角不等式：dist(s,z)+dist(z,h)>=dist(s,h)
我们对此设计的贪心算法能够用于任何满足这三条性质的距离函数，而且他也依赖于这3条性质。
2.2 算法设计与分析
我们最容易想到的贪心算法是把第一个中心选在只有一个中心时的最佳可能位置，然后依次添加中心，使得覆盖半径尽可能的缩小。
但是上述的贪心策略在某些情况下会导致非常坏的结果。
例如下面这个例子：
只有两个地点s和z，并且k=2，此时上述算法会得到较差的结果。
我们假设已知最优解，那么对于任意一个地点s，一定有一个中心c属于C，覆盖地点s，且距离不超过最优半径r。我们这里考虑用s代替c，通过将半径扩大到2r来覆盖c所覆盖的地区。（三角不等式）
算法如下：
S'表示还需要覆盖的所有地点
初始化S=S'
令C=空集
while S'不为空集
我们任意选择一个s属于S' ，把s加入到C
从S'中删去与s距离不超过2r的所有地点
endwhile
if(|C|<k then
return C
else
不存在半径不超过r的k个中心的集合
endif
证明：假设不成立，那么有一个不大于k的中心集C*，它的覆盖半径rc<=r。上述算法中选择的c，一定有dist(c,c*)<=r
接下来我们要证明的是对于C中的两个不同的中心，没有一个中心c能够靠近这两个节点。具体证明可用三角公式：
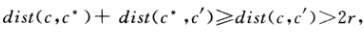
所以得到不存在，所以|C|>=|C|>k
所以得证。
上述算法是我们已知最优半径，那么在未知最优半径时如何考虑呢？
第一种：我们猜测最优解的大小。我们对于算法中的两种情况：1.找到一个半径不超过2r的k个中心的集合 2.得出结论没有覆盖半径不超过r的解。
我们先用两个点间最大的距离rmax/2来运行，此时算法会有两种情况。
我们对于这两种情况可以用不同的猜想值。对于第一种，我们可以猜想更小的半径r
另外一种，我们猜想更大的半径值r.
对于每一次的迭代，我们都考虑r0和r1两个值，代表最优半径大于r0小与2r1，算法的终止应该是r0与r1接近，我们就知道了最优半径接近于r0
第二种：我们可以巧妙的绕过假设已知半径。
在未知r时，我们考虑选择与之前选择的中心里的最远的地点S，如果有离前面选择中心不小于2r的地点，那么这个最远的地点s一定是它们中的一个。
设k<=|S|
任意选择一个地点，令C={
s}
while|c|<k
选择一个地点s使得sC最大
把s加入到C中
endwhile
return C
证明见P427
三、集合覆盖：一般的贪心启发式方法
本节考虑一个在第八章出现过得问题集合覆盖问题。
3.1 问题
我们回想之前看考虑的集合覆盖问题。它给定n个元素的集合U和一组U的子集和S1，S2.。。Sn，如果这些子集中的若干个的并集等于整个U，那么就称这若干个子集是一个集合覆盖。
现在，我们对于每一个子集Si关联一个权Wi，我们的目标是找一个集合覆盖使得权重最小。
3.2 算法设计
我们现在需要开发解决这个问题的一个贪心算法。通过每次选取一个集合来使得我们的结果朝着目标迈进一步。这里有两个重要的参数，一个是权值，另一个是覆盖的元素个数。但是其中的任何一个都不是好的贪心指标，所以我们这里采用两者结合采用Wi/|Si|。
所以算法如下：
开始是令R=U并且没有被选择的集合
whileR ！=空集
选择wi/|si交R| 最小的集合si
从R中删去集合si
endwhile
return 所有被选择的集合si
但该算法依旧存在问题。
例子如下：
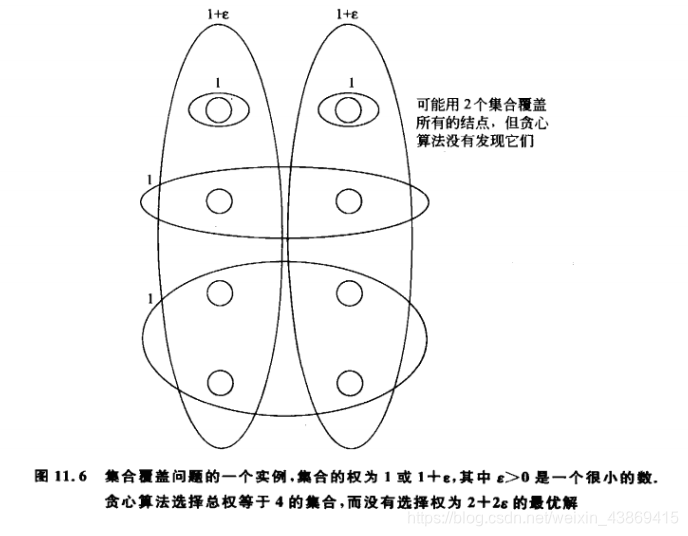
3.3 算法分析
我们考虑cs=wi/|si交R|
其中H函数为调和函数。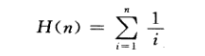
四、定价法：顶点覆盖
我们现在考虑定价法。正如第八章所说的那样，顶点覆盖实际上是集合覆盖的特殊情况。
4.1 问题
顶点覆盖问题：给定图G=（V,E），其中一个集合S属于V，使得每一条边至少有一个端点在集合S中。我们在这里给定每一个顶点一个关联的权值wi，目标是找到一个权值最小的顶点覆盖S。
在开发设计算法前，我们考虑能够利用归约做近似吗？
我们已经知道顶点覆盖很容易归约到集合覆盖。那么我们能否从上一节的集合覆盖问题所提出的算法中得到什么相关的信息？
首先我们考虑无权的情况。因为顶点覆盖可以归约到集合覆盖，所以这意味着我们能够利用集合覆盖的近似算法给出带权的顶点覆盖问题的Hd近似算法。
具体结论如下：
证明：我们已经证明了顶点覆盖<=P集合覆盖,这个归约也可以推广到带权的情况。
我们定义集合覆盖如下：基础集U，对于每一个顶点i，定义集合Si由所有的与顶点i关联的边组成，他的权重等于wi。由此集合覆盖转变为顶点覆盖。其中si的大小为点的度数。由此得证。
我们可以知道当d较小时，上述算法性能较好，但当d较大时，他会变差。
注意并不是所有的归约都能设计近似算法。
例子如下：
4.2 算法设计：定价法
最小化费用的定价法：我们将顶点的权看做费用，并认为每一条边必须为找到的顶点覆盖支付它的一份费用。
我们首先选择一个顶点i覆盖所有与i相关联的边，我们假设所有边支付的总和小与wi则认为是公平的。
证明：对于每一个顶点i属于S*，总是公平的。那么下述成立：
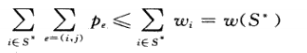
由于每条边至少对坐班的表达式贡献一个pe，所以左边至少和所有的价格pe之和一样大，证毕。
如果
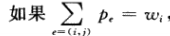
那么就趁顶点i是紧的。（付清的）
Vertex-Cover-Approx(G,w)
对所有的e属于E，令pe=0
while存在边e(i,j) 使得i和j都不是紧的
选择这样一条边e
在不违反公平性的条件下加大pe
endwhile
令S是所有紧顶点的集合
return S
4.3 算法分析
考虑当一条边的两个顶点都在集合中时，那么该边支付了两次。在上述算法中，每条边最多被要求支付两次。
五、用定价法最大化：不交路径问题
5.1 问题
给定有向图G以及k对节点（s1,t1）(s2,t2)…(sk,tk)和整数容量c，我们把每一对(si,ti)看做一个路由请求，他要求一条从s1到t1的路径。我们所求的解包括需要满足的请求自己，以及满足这些请求的路径，并且没有一条超载的边。
我们认为对于每一个请求i，有一条从si到ti的路径pi，并且每一条边最多被c条路径使用。目标是求|I|的最大解。
我们可以发现当c==1时，问题为求不交路径。
5.2 算法设计
我们首先考虑当c=1时的一个简单的算法。
算法如下：
Greedy-Disjoint-Paths
令I=空集
while 没有新的路径
设pi是与前面选择的路径边不交的、连接还没有被连接的某对si,ti的最短路径（如果有的话）
把i加入到I，选择路径Pi连接si和ti
endwhile
其中m为图的边数。
证明：我们考虑最优解I*，对于每一个i属于I*，pi是它对应的路径。
同时我们设I是算法返回的对应解。我们考虑图中有至少根号m条边的路径是长的，否则是短的。我们设Is为I中表示短的路径的集合，Is为I中短路径的集合。
因此I中最多有根号m条路径是长的。
如果I比I大，那么考虑短路径pi，贪心算法在选择长路径之前应该考虑这条路径，而不存在只可能因为有一条边e在之前的pj中已经被选择，我们称这条边e阻止路径pi*
我们可知}pj}<=|pi*|<=根号m，并且pj中的每一条边至多阻止一条路径。
由此得到每条短路径最多阻止最优解中的根号m条。
从而得到以下式子：
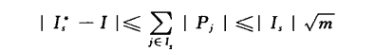
同时I*有以下三类路径组成：
1.长路径
2.在I中的路径
3.不在I中的短路径，不超过|Is|*根号
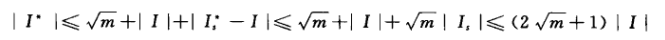所以得证。
5.3 设计与分析一个定价算法
我们现在考虑允许c>1时的情况。
采用定价法的思路：我们认为路径必须为消耗边付款，每条边由单位成本，同时为了让算法摊开它的路径，不要总是选择一条边，我们考虑增加乘法参数，每用一次便增加它的长度。
算法如下：
Greedy-Paths-with-Capacity
令I=空集
对于所有的e属于E，令边的长度le=1
while 没有新的路径
设Pi是连接尚未连接的点对（si,ti），并把它加入选中的路径集合后没有一条边使用尝过c次的最短路径
把i加入I，选择路径Pi连接si到ti
Pi上所有边的长度乘以β
endwhile
分析：我们与之前的分析类似，这里对于短路径的定义需要根据情况而定，假设此时C=2那么我们认为当边长小与β^2时为短路径。
算法保证了不会有三条路径同时选择一条短路径，因为当第三条选择是边e已经是β^2了，根据定义它为长路径。
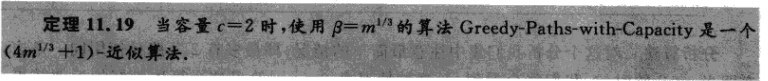证明：我们对于所有I*-I中的路径长度求和可得如下：
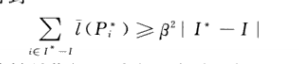
由于每一条边最多被最优解I*中的两条路径使用所以：
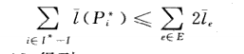
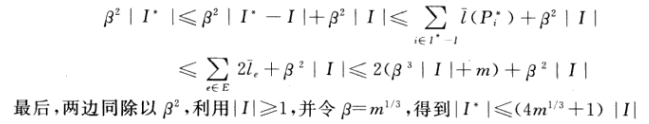
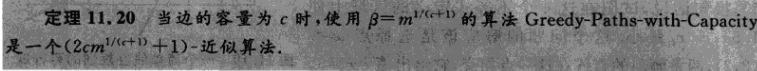
注意：本算法适用于任意容量c>0的不交路径问题。其中选择被β=m^1/c+1 并认为小与β^c的路径是短路径。
六、线性规划与舍入：对顶点覆盖的应用
6.1 线性规划
线性规划：
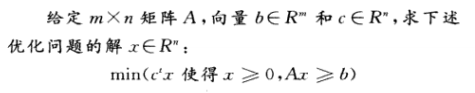
我们称C^t x是线性规划的目标函数，Ax>=b是一组约束。
（内点法，单纯形法？）
6.2 顶点覆盖作为一个整数规划
我们考虑给出一个与顶点覆盖问题紧密对应的线性规划。
考虑每一个顶点i带有权wi>=0的图G=（V,E）线性规划以使用变量向量为基础。这里对每一个点i有一个决策变量x来模拟i是否包含在顶点覆盖的选择中。
(x=0表示顶点i不在这个选择中）
因此我们可以引入一个n维向量x，它的第i个坐标对应第i个决策变量xi。
我们用线性不等式来描述构成顶点覆盖的需求，同时用目标函数来使得整个的权最小的目标。对于每一条边(i,j），我们写成xi+xj>=1
总而言之得到对应的线性规划形式的描述如下：
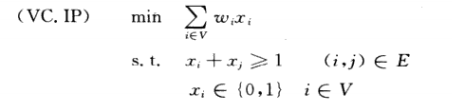
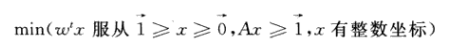
此时上述问题被称为整数规划。
6.3 把线性规划应用于顶点覆盖
对于整数规划问题是NP的，但如果我们将其中x必须取整数这个约束条件去掉，那么这就变成了一个线性规划问题。
其中wlp是线性规划得到的最小值。
我们对于线性规划的解采用舍入的方式即四舍五入法。
此时得到的S集合有以下性质：
七、再论负载均衡：一个更高级的LP应用
本节我们考虑一个更为一般的负载均衡问题，我们采用和上述类似的算法利用线性规划来得到近似算法。
7.1 问题
我们现在对于之前所说的问题加上一个约束条件，即对于每项作业有一个机器中的子集，他只能被分配给这个子集中的机器。我们的目标未变，依旧是要求所有机器上的负载最小。（广义负载问题）
7.2 算法设计
我们考虑用整数规划和线性规划来进行描述：
我们用变量xij来对应每一对机器i属于M和作业j属于J。令xij=0表示作业j没有分配给机器i。令xij=tj表示作业j的全部负载tj都分配给机器i。
因此我们可以把x看做一个mn维向量。
具体可以如下：
然后我们将要求放低，即0=<xij<=tj
由之前的结论我们可以知道：
但在这里我们对于舍入做一点改变。
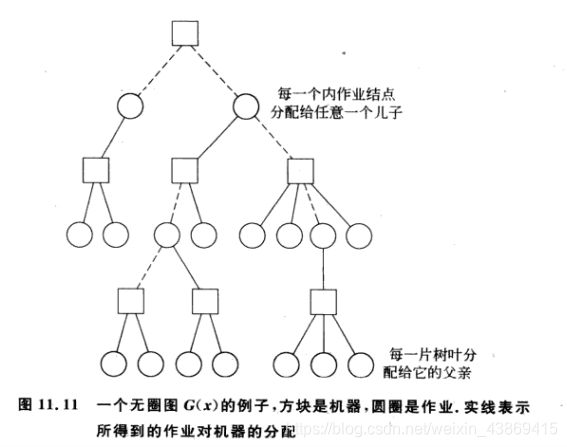
由此我们要考虑如何在线性规划的解中消去圈。
我们考虑一下这个网络流：
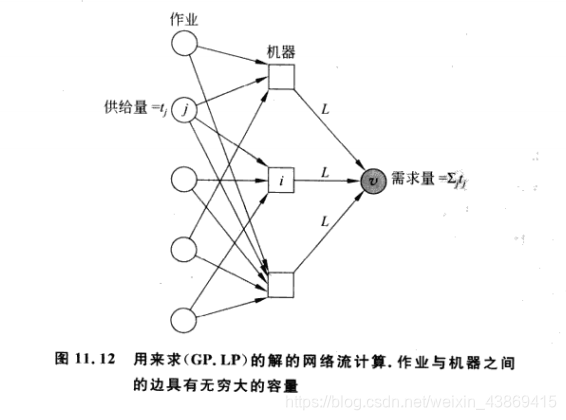我们需要在Gx中修改解以消去Gx中的圈，其中Gx是忽略掉G的边的方向，删去汇点v以及所有关联的边。删去所有从j到M中不带流量的边所得到的的图。
我们在每一步中删去Gx的一条边并且不增加负载L，也不引入任何新的边。（网络流中的augment算法）
八、任意好的近似：背包问题
在实际中，许多人会考虑对于NP完全问题给出一个与最优解不超过百分之1的近似解。
从这个观点来看，我们之前的算法是相当弱的。
8.1 问题
这里我们考虑一个简单的问题：假设有n件物品，你考虑把他们装入到一个背包中，每一件物品i有两个整数参数，重量wi和价值vi。我们给定背包的总容量W，目标找到一个物品子集有最大的价值。
在这个问题上我们考虑给出一个非常强的近似算法。
那么我们如何去得到我们算法的精度呢？我们希望算法能够找到一个最优值不低于最大的1/(1+x)，且算法在多项式时间内运行，但对x的依赖不是多项式的。（多项式时间近似方案）
8.2 算法设计
对于v值小的情况我们直接考虑动态规划，但对于v值较大时，我们可以考虑将价值变为舍入参数b的整数倍，然后采用动态规划进行解决。
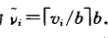
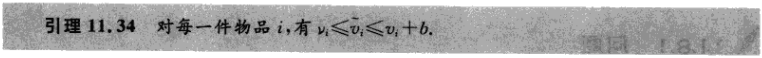
Knapsack-Approx（x）
b=(x/n)maxivi
解价值为vi的背包问题
return 找回的集合
8.3 算法分析
证明：
8.4 新动态规划算法
我们可以知道当重量较大时，子问题的规模较大，所以我们将子问题改为OPT（i,V）
其含义为：能够得到价值不小于V的解的最小背包重量。
由此我们将问题改为OPT（n,V）<=W
由此我们得到算法如下：
Knapsack(n)
M[0-n,0-V]
for i in 0,n
M[i,0]=0
endfor
for i in 1,n
for v in 1,1-i的v的总和vj
if V> vj then
M[i,v]=wi+M[i-1,V-vi]
else
M[i,v]=min(M[i-1,v],wi+M[i-1,max(0,V-vi)]
endif
endfor
endfor
return M[n,V]
此时算法需要O（n^2 v）