连续系统的时域分析
LTI连续系统的响应
连续系统的表示
1. 二阶常系数线性微分方程
在上一章中我们对系统进行分类的时候即说过,对于线性时不变性系统,可以用【常系数线性微分方程】来对系统进行数学建模。

2. 相似系统
“能用相同的数学方程描述的系统称为相似系统”

其本质就是将具体的现实系统用抽象的数学语言进行描述,这样更容易发现系统之间的共性,也可以类比移植研究方法。
3. 微分方程的模拟框图
(1)基本运算↔基本部件

(2)模拟框图
将微分方程用基本部件的相互联接表征出来的图即称作框图。
(3)微分方程→系统框图
①输入信号只有f(t)
【方法论】
因为使用积分器来表达微分运算,所以要注意积分运算和微分运算的互逆特性。
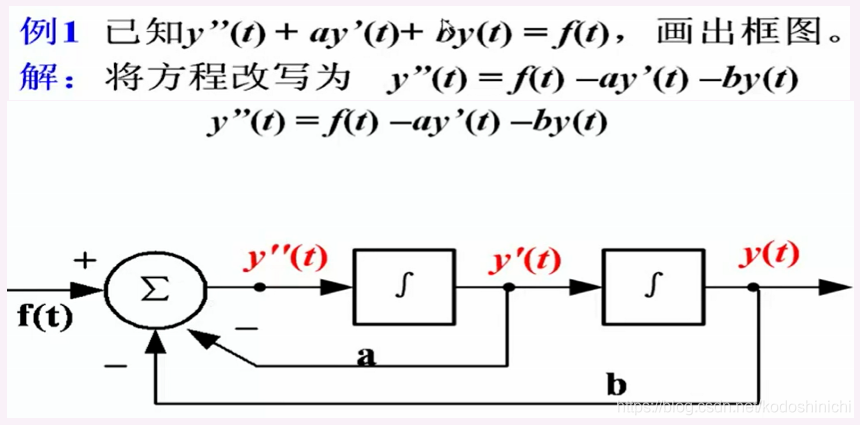
对于一个微分方程的通式【y’’(t)+a1y’(t)+a0y(t)=f(t)】要转换成【y’’(t)=-a1y’(t)-a0y(t)+f(t)】的形式,yn(t)通过积分器即可得到yn-1(t)
①最高阶为几阶导数,系统就是几阶的,就要相应使用几个积分器;
②将最高阶的导数项写在最左边积分器的最左侧
③以最右边的积分器的输出作为y(t)
②输入信号是f(t)的组合形式
【方法论】
如果想要利用积分器来表示f’(t)与f(t)之间的关系,就需要再增加一个积分器,但这样就会违背【系统有几阶就使用几个积分器】的原则。
对于形如【y’’(t)+a1y’(t)+a0y(t)=af(t)+bf’(t)】这样的系统
①先构造一个响应x(t),该x(t)对应系统【:
】的响应
②再根据LTI系统的线性性以及微分特性,可以得到,原系统的响应y(t)=ax(t)+bx’(t)

(4)系统框图→微分方程
【方法论】
①找准求和器,求和器隐含着等式关系
②如果输出的响应信号y(t)前还设有一个求和器,则需要引入辅助变量x(t),x(t)设立在最右边的积分器的输出位置;于是可以根据积分器的运算关系陆续推出各个节点的信号
③逆向使用LTI系统的线性性和微分特性:
根据框图的关系得到了x’’(t)+a1x’(t)+a0x(t)=f(t),然后又有y(t)=ax(t)+bx’(t);
那么便可组合得到y’’(t)+a1y’(t)+a0y(t)=af(t)+bf’(t)

微分方程的经典解法
1. 经典微分方程的解结构
齐次线性微分方程(LTI系统的数学模型就是齐次线性微分方程)的通解=齐次解+特解

2. 微分方程齐次解的形式

3. 微分方程特解的形式

4. 示例

连续系统的响应
- 连续系统的初始值和初始状态
- LTI连续系统的零状态响应
- LTI连续系统的零输入响应
- LTI连续系统的响应的分类
1. 初始值与初始状态
(1)概念介绍
①初始值:n阶系统在t=0时接入激励,其响应在t=0+时刻的值,即y(j)(0+)(j=0,1,2,…,n-1)
②初始状态:系统在激励尚未接入的t=0-时刻的响应值y(j)(0-)j=0,1,2,…,n-1),这个值反映了系统的历史情况,而与激励无关。
在求解微分方程的时候往往需要初始条件来代入求解未知系数,因此我们需要从已知的初始状态y(j)(0-)中求出初始值y(j)(0+)。
(2)从初始状态求解初始值
①方法论
如果激励f(t)中含有冲激函数及其导数,那么当t=0时激励接入系统时,响应及其导数从y(j)(0-)值到y(j)(0+)值可能会发生跃变。因此需要我们掌握方法从初始状态求解出相应的系统初始值。
- 将输入f(t)代入微分方程,根据【等式两端各奇异函数的系数相等】的原理,可以得到方程左端y(t)的最高阶导数中含有δ(t)的最高阶导数。
- 假设等式右端δ(t)的最高阶项为δn(t),那么可设yn(t)=anδn(t)+an-1δn-1(t)+…+a0δ(t)+r0(t),其中r0(t)中不含有δ(t)及其各阶导数
- 对yn(t)进行逐次积分,得到yn-1(t),…,y(t),将这些项全都代入微分方程中,根据方程等号两端奇异函数项的系数相等的原则,从而可以求得所有的未知待定系数
- 最后再将所有确定了的各阶导数yn(t),…,y’(t)关于[0-,0+]区间进行积分,即可以求得n阶微分方程的n个初始值。
若yn(t)的式子中含有冲激导数或其各阶导数,则说明函数yn-1(t)在[0-,0+]区间中发生了跃变;反之,如果某个函数的导数不含有冲激函数及其各阶导数,就说明该函数在区间[0-,0+]中不发生跃变。
②示例

2. 零输入响应
(1)定义
零输入响应yzi(t)(yx(t))是激励为零时仅由系统的初始状态{x(0)}所引起的响应。
在零输入的条件下,系统对应的数学方程应该是一个齐次线性微分方程。
(2)零输入状态的初值条件
因为零输入状态下不对系统加入任何激励,那么在t=0这一刻系统自然不会发生任何状态的突变。且在t=0-时刻,按照初始状态的定义,y(j)(0-)反映的也是该时刻系统的所有历史数值。
故有 y ( 0 − ) = y z i ( 0 − ) = y z i ( 0 + ) y(0_-)=y_{zi}(0_-)=y_{zi}(0_+) y(0−)=yzi(0−)=yzi(0+)

(3)零输入响应的求解
①方法论
- 将y(t)=0代入系统,得到系统相应的零输入状态下的齐次线性微分方程组
- 按照上述结论求得相应的零输入初始值
- 按照齐次线性微分方程组的求解方法,求解特征方程,得到相应的通解形式,并利用初始值求解待定系数。
②示例

3. 零状态响应
(1)定义
零状态响应yzs(t)(yf(t))是系统的初始状态为零时,仅由输入信号f(t)所引起的响应。
在零状态的条件下,LTI系统对应的数学方程仍然是一个非齐次线性微分方程。
(2)零状态情况下的初值条件
因为是零状态,根据【初始条件】的定义可知系统在0-及之前的时刻没有任何的历史信息。也就是说零状态响应在0-时刻的各阶数值都为0.
故有 y z s ( j ) ( 0 − ) = 0 , j = 0 , 1 , . . . y_{zs}^{(j)}(0_-) = 0,j=0,1,... yzs(j)(0−)=0,j=0,1,...
但是我们求解通解的待定系数需要的是【初始值】,所以需要用到前文中【从初始状态求初始值】的待定系数法进行求解——将f(t)=ε(t)代入原微分方程,求出yzs(j)(0+)和yzs(j)(0-)之间的关系。
(3)零状态响应的求解
本质上和求解一个非齐次线性微分方程组的通解是一样的。
①方法论
- 将f(t)=ε(t)代入微分方程,按照系数匹配法求得系统的各阶初始值
在上式代入了将f(t)=ε(t)的基础上,令t>0——此时δ(t)=0,ε(t)=1
- 根据特征方程,求得零状态响应中的齐次部分的形式(此时含有未知系数)
- 根据激励的形式,确定零状态响应中的特解部分的形式,并将特解代入上述方程,可以求出未知系数
- 将特解和齐次解合并(得到的即为零状态响应的通解,且其内含有齐次部分的未知系数),再代入上述方程,根据【等式两边相同项的系数对应相等】的原则求解出剩下的未知系数。
②示例

4. 响应的分类
我们可以从三个角度去划分一个系统的响应。
①零输入响应和零状态响应
之前在讲述系统的线性性质的时候曾说过,对于一个LTI系统,全响应=零输入响应+零状态响应。
这是从作用于该系统的激励的角度来进行分类,将系统的响应划分成系统的历史状态引起的和外加输入信号引起的。
②固有(自由)响应和强迫响应
- 固有响应:仅仅与系统本身的特性有关,与激励的函数形式无关。比如说方程的齐次解(yh(t))的形式仅仅由特征方程的根确定,所以齐次解往往就被称作是系统的【固有响应】,而特征方程的根相应称作系统的【固有频率】。
- 强迫响应:与激励的函数形式有关,比如微分方程的特解(yp(t))形式往往需要根据激励的函数形式来确定。
③暂态响应和稳态响应
- 暂态响应:响应中暂时出现的分量,随着时间的增长,该部分将会消失
- 稳态响应:稳定的分量,如果存在则通常表现为阶跃函数和周期函数。e.g. 电路系统中的直流稳态响应和正弦稳态响应。
【响应分类的示例】

基本信号响应的定义与求解
讲述信号系统中的两类典型信号:冲激信号和阶跃信号,作用于系统时,系统会有怎样的响应。
p.s. 值得注意的是,冲激响应和阶跃响应都是零状态响应。
冲激响应的定义与求法
1. 冲激响应的定义
对一个LTI系统,当其初始状态为零时,输入为单位冲激函数δ(t)所引起的响应即为(单位)冲激响应,表示为h(t)。
一言以蔽之,冲激响应是激励为单位冲激信号δ(t)时系统的零状态响应。
h ( t ) = T [ 0 , δ ( t ) ] h(t)=T[{0},δ(t)] h(t)=T[0,δ(t)]
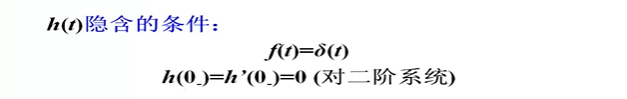
2. 冲激响应的求法

3. 示例

阶跃响应的定义与求法
阶跃响应的求解与冲激响应的求解思路大同小异,只不过作用于系统的信号性质不同,读者在学习此处内容时可以与上文进行类比。
1. 阶跃响应的定义
对一个LTI系统,当其初始状态为零时,输入为单位阶跃函数ε(t)所引起的响应即为(单位)阶跃响应,表示为g(t)。
一言以蔽之,冲激响应是激励为单位阶跃信号ε(t)时系统的零状态响应。
g ( t ) = T [ 0 , ε ( t ) ] g(t)=T[{0},ε(t)] g(t)=T[0,ε(t)]
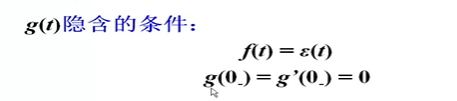
2. 阶跃响应的求法

3. 示例

4. 冲激响应与阶跃响应之间的关系

信号的卷积
信号的【卷积】是一种很重要的运算,我么学习它的思路是——利用卷积将输入信号分解成众多的冲激函数之和(或积分)的形式,利用前面所学的冲激响应,求解LTI系统对任意激励的零状态响应。
由此可知,【卷积的本质是分解】。
信号的时域分解
所谓的【信号分解】就是把信号f(t)分解成基本信号δ(t)和ε(t)的线性组合。
1. 门函数的表示

2. 任意信号的分解

- 首先,我们使用fhat(t)来近似f(t),是采用了微积分中的微元思想,用很多的锯齿状的折线段来逼近原函数,当折线段的间隔取得越小,拟合就越精准;
- 注意体会f(△)△p(t-△)的含义,其本质就是将一个门函数在f(t)曲线上进行移动和升降操作,使之尽量贴合原曲线;
- 因为要使得fhat(t)=f(t),需要用到极限的运算,在极限运算下——离散量变成连续量,间隔量变成微元,求和变成积分。
在后续的课程中,我们马上就会学到,上图最后得到的积分式子,就可以定义成f(t)与δ(t)的卷积操作。
这也进一步验证了【卷积的本质就是信号的分解】。
卷积积分的定义与求解
1. 理解——定义【卷积】是为了完成信号的分解
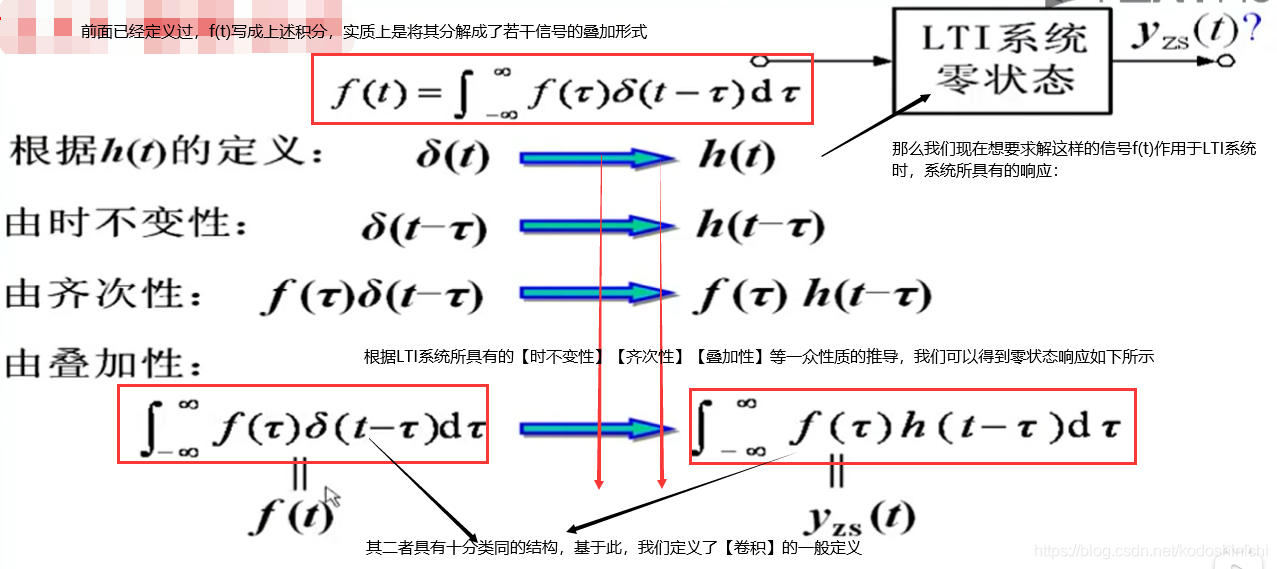
2. 卷积积分的一般定义

【卷积的运算小技巧】
在定义式中积分运算是在(-∞,+∞)的积分限中完成的,但实际运算中f1(t)和f2(t)往往都含有阶跃或者冲激的成分,所以可以根据这些基本信号的性质调整上下限:
一句话概括,就是f1(t)影响积分的下限,f2(t)影响积分的上限。
3. 计算示例

4. 卷积积分的图解法
(1)方法论

(2)过程理解
把握图解法求解卷积积分,需要理解以下两点:
①使用图解法是为了更加清晰直观地确定积分运算的上下限,而被积函数是不变的。
②卷积积分只有当f1(t)和f2(t-τ)这两者的函数图像有重叠的时候才有值
③卷积积分的集合意义并不是两个图像重叠部分下的面积,而应该是重叠部分下f1部分的面积乘上f2部分的面积。

(3)评价
- 图解法主要是解释卷积的过程,只适合简单的函数图像
- 使用图解法可以方便求解某一时刻的卷积值

卷积积分的性质
1. 卷积积分的代数性质

2. 复合系统的冲激响应
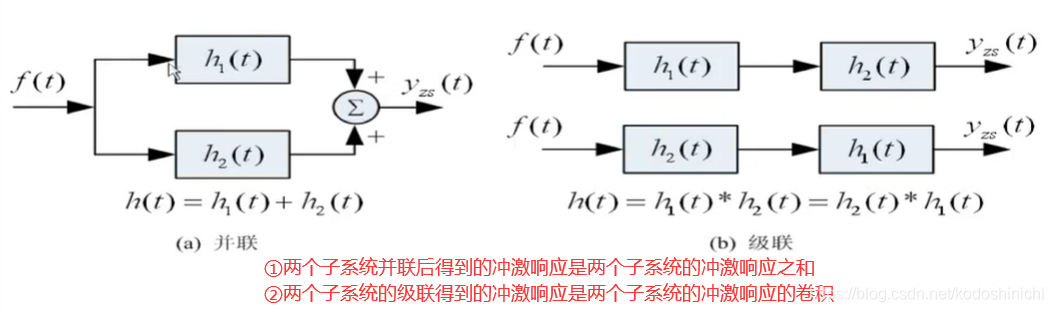
【理解】
- <并联>因为零状态响应具有线性性质,所以并联是将两个子系统单独的冲激响应相加
- <级联/串联>而在串联中,经过第一个系统得到的输出,同时是第二个系统的输入,根据前文在【卷积积分的定义】中讨论的零状态响应的一般式,可知将两个系统的冲激响应进行卷积运算即可得到最终系统的响应。
3. 奇异函数的卷积特性

4. 卷积运算的微积分特性
(1)性质描述

(2)示例——求解两个函数的卷积积分f1(t)*f2(t)
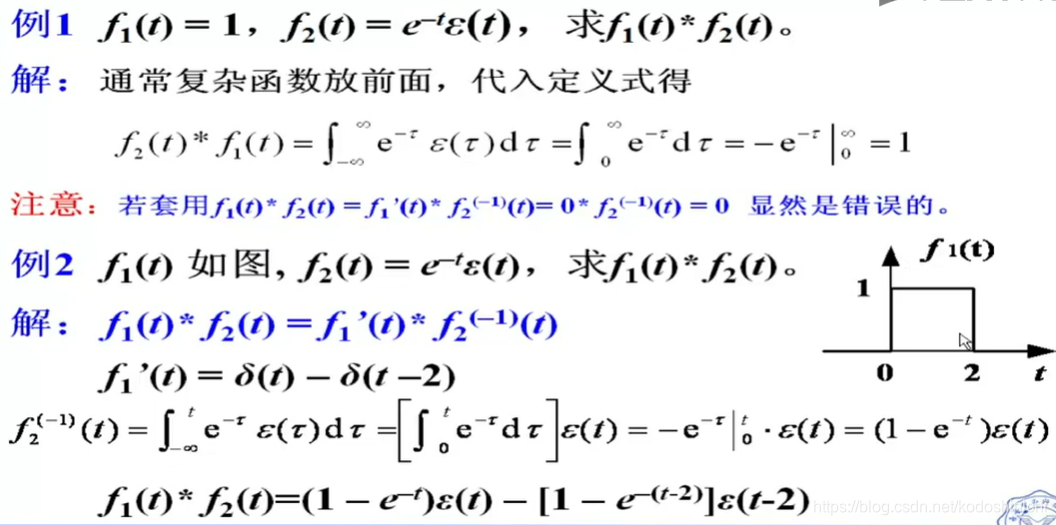
【方法论】-怎样求解两个函数的卷积运算?
- 使用卷积运算的定义进行求解,选择好合适的f1(t)和f2(t)代入式子中,注意应尽量选择形式简单的函数作为f2(t),因为在卷积的时候需要对f2进行f2(τ-t)的运算。
- 使用卷积运算的微积分性质第三点进行运算,但是要注意验证该性质成立的条件是否满足。
5. 卷积运算的时移特性

信号卷积的求解
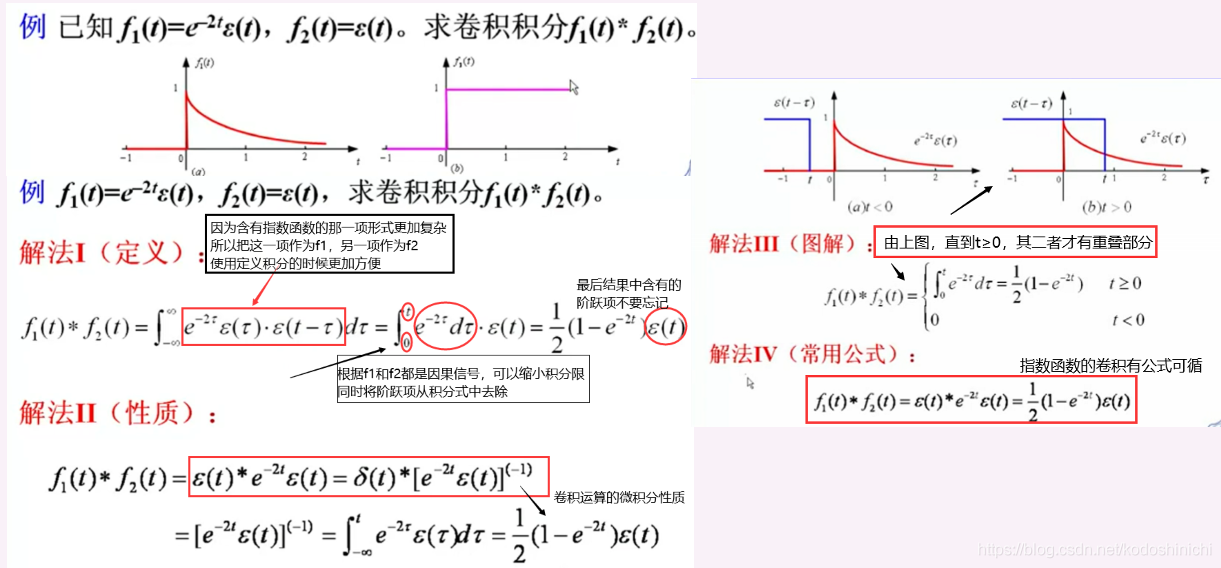
1. 常用的卷积公式

2. 卷积的求解方法
(1)方法论

(2)示例
利用卷积产生信号波
1. 周期信号的产生
(1)梳状函数的定义
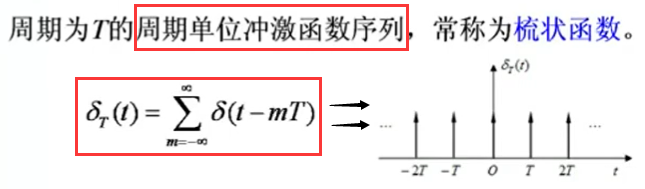
(2)利用梳状函数产生周期函数

2. 矩形波的卷积
(1) 结论: 两个门函数的卷积结构是一个梯形波、
- 特别地,当两个门函数的门宽相同时,得到的就会是一个三角波
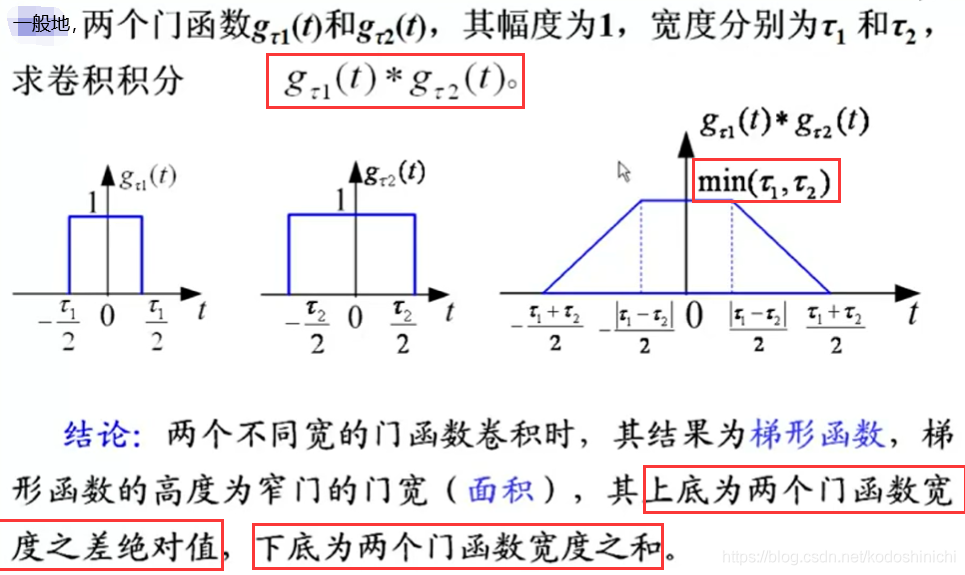
(2)示例,理解
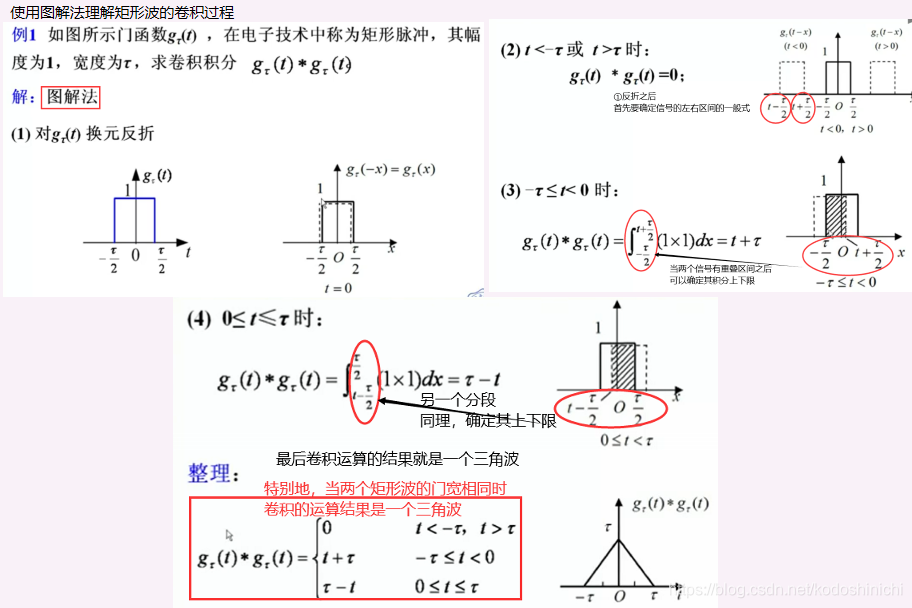
卷积与相关
1. 互相关与自相关
为了比较某个信号和另一个延时τ信号之间的相似度,需要引入相关函数的概念。
相关函数是用于鉴别信号的工具,其也称为相关积分,与卷积的运算方法类似。
(1)互相关函数
- 定义:给定两个实函数f1(t)和f2(t),若其二者为能量有限信号,则:

- 含义:互相关函数是两个信号之间时间相差τ的函数。
一般来说,R12(τ)≠R21(τ);R21(τ)=R12(-τ)
R21(τ)=R12(-τ)和R12(τ)=R21(-τ)都是成立的,其含义理解如下:
2函数比1函数领先一个τ相当于1函数比2函数落后一个τ(领先一个-τ)。
(2)自相关函数
- 定义:如果互相关定义中的两个函数f1(t)和f2(t)是同一信号,则无需区分R12和R21

- 含义:互相关函数衡量的是两个不同的信号相差某一时延的相关程度,自相关函数衡量的是同一个信号自身相差某一时延的相关程度。

2. 相关v.s.卷积
(1)相关运算与卷积运算的定义比较

(2)相关运算与卷积运算的图示对比
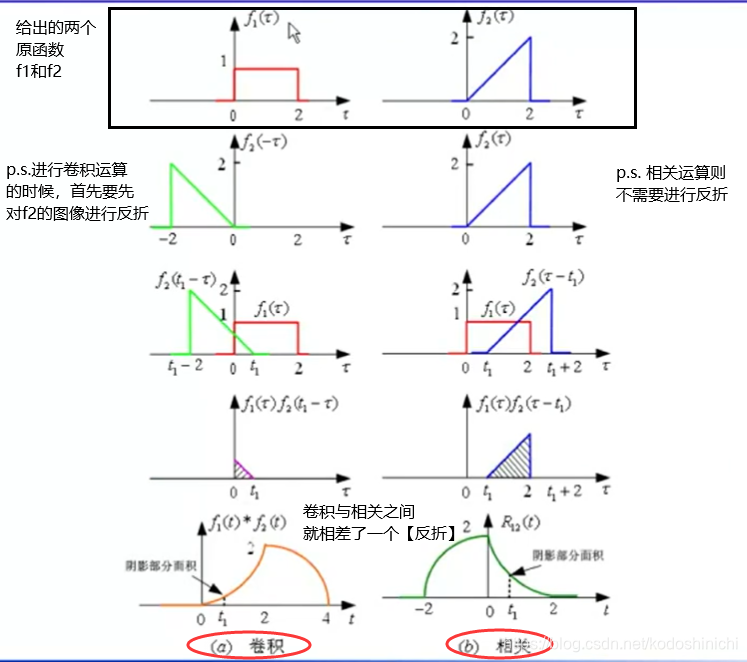
(3)卷积与相关的性质
- 相关运算不需要进行反折,直接进行积分即可
- 卷积与相关运算就相差一个【反折】操作
- 如果进行卷积(或相关)运算的两个函数都是偶函数,那么卷积和相关的操作是相同的

微分算子模型
这一节是从另一个角度来说明这一章的整个内容,读者可以将这一部分作为整章内容的回顾与梳理。
微分算子的定义

注意:这里P和(1/P)都只是代表一种运算标志,并不是变量符号。
【例】使用微积分算子来描述线性微分方程

微分算子的性质
1. 正幂多项式可以因式分解

2. 正幂因式的乘法满足交换律
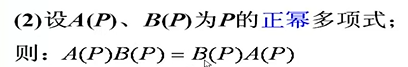
3. 微分算子等式两边的共同因式不能随意消去

4. 原函数=先积分再微分≠先微分再积分

传输算子

本质上,用H§来代替原先的微分方程,且其二者是一一对应的。
