系统的时域分析,主要包括下面三个内容:
- 线性时不变系统的描述及特点
- 连续时间LTI系统的响应
- 离散时间LTI系统的响应
在求解系统的响应的时候,不对系统的物理量进行任何的变换,而是在时域里面直接进行独立的变量分析,这种方法叫做时域分析法。时域分析法的特点是非常直观、物理概念非常清晰,它也是进一步学习其他变换域分析法的基础。在时域分析法里,连续变量用t来表示,离散变量用k来表示。
1. 线性时不变系统的描述及特点
连续时间系统的数学描述

互不相同的物理系统,描述系统输入输出的微分方程的形式却可以相同。

- 等号左边:响应及各阶导数线性叠加(最高阶n)
- 等号右边:激励及各阶导数线性叠加(最高阶m)
离散时间系统的数学描述
[例1] 假设某人从当月起,每月初到银行存款x[k]元,月息为r,设第k个月末总存款为y[k]。试写出描述总存款数y[k]与月存款数x[k]关系的方程式。
这是一个银行零存整取的例子,我们分析一下第k月末总存款由哪几部分组成:
- 首先第k月初之前有一个总存款数,也就是y[k-1]
- 其次是第k月初存入的款数x[k]
- 再有就是第k月初之前的总存款数y[k-1]经历了第K月产生的利息,r·y[k-1]。
也就是说,第K月的总存款数由这样三个部分组成,也就是:
- y[k] = y[k-1] + x[k] + r·y[k-1]
把这个方程整理一下,把跟y有关的挪到等号左边,等号右边只有x[k]:
- y[k] - (1 + r) · y[k-1] = x[k]
最后,这个方程就成为一阶常系数后向差分方程。
[例2] 某地区在第k年人口总数为y[k],人口正常出生率和死亡率分别为a和b,而第k年从外地迁入人口为x[k],写出描述第k年人口总数y[k]的方程式。
第k年人口总数y[k],包括这样几个部分:
- 第k年之前也就是K-1年人口总数 y[k-1]
- 第k年出生的人口总数系数a乘以前一年的人口总数,也就是 a·y[k-1]
- 第k年死亡的人口总数,也就是 b·y[k-1]
- 最后一部分是第k年从外地迁入的人口 x[k]
最后可以得到:
- y[k] = y[k-1] + a·y[k-1] - b·y[k-1] + x[k]
整理一下:
- y[k] - (1 + a - b)·y[k-1] = x[k]
显然,这也是一个一阶常系数后项差分方程
从上面的几个例题,我们可以看出,互不相同的物理系统,描述系统输入输出的差分方程的形式却可以相同。

- 等号左边:响应及各阶差分线性叠加(最高阶n)
- 等号右边:激励及各阶差分线性叠加(最高阶m)
线性时不变系统
用差分方程近似表示微分方程
在物理系统中,连续系统和离散系统是有一定的关系的,连续信号我们可以用微分的形式来表示,相应的离散信号可以用差分的方式来表示。描述一个连续系统可以用微分方程来描述,那么离散系统可以用差分方程来描述,那么如何将连续系统的微分方程,用离散系统的差分方程来近似呢?
下面以一个一阶的LR电路为例来说明:

这是一个电感电阻的串联电路,其中的输入是电压源x(t),输出是回路的电流i(t),为了表示方便,系统的响应统一用y(t)来表示。根据基尔霍夫电压定律可以得到LR电路的方程,也就是总的电压源x(t)等于电感上的电压加电阻上的电压
线性时不变系统由线性常系数微分方程/差分方程描述
线性包括均匀性和可加性两部分,同时具有均匀性和可加性的系统称之为线性系统。
系统的时不变性由微分方程或者差分方程的系数来决定,如果是常系数,则为时不变系统,如果是变系数,则为时变系统。

微分、差分、积分和求和运算,都是线性的
微分的运算其实包含着加减乘除,积分是求和取极限,差分是平移相减,求和是平移叠加。
下面来看一道例题:
已知一个连续时间线性时不变系统,在x1(t)的激励下,产生了响应为y1(t),求该系统在x2(t)激励下产生的响应y2(t)。
 左图是一个单位阶跃信号,也就是输入信号x1(t),在它的作用下,y1(t)是一个指数信号。
左图是一个单位阶跃信号,也就是输入信号x1(t),在它的作用下,y1(t)是一个指数信号。
那么另外一个输入信号x2(t)是一个斜坡信号,我们可以看出,x1(t)和x2(t)的关系,也就是斜坡信号是阶跃信号的积分。
既然第二个输入信号是第一个输入信号的积分,对于已知的系统为线性时不变系统,这样一个系统,在第二个信号的作用下,得到的响应y2(t)也应该是y1(t)的积分。
 这道题使用的原理就是线性时不变性
这道题使用的原理就是线性时不变性
2. 连续时间LTI系统的响应
对一个系统来说,响应的时域求解方法主要有以下几种:
- 第一,经典法,也就是求解微分方程;
- 第二,卷积法。系统的全响应可以分解为零输入响应和零状态响应之和
零输入响应可以用解齐次微分方程的方法得到
零状态响应可以通过求卷积积分的方法得到
连续时间LTI系统的零输入响应
零输入响应是指输入信号为零,仅由系统的初始状态单独作用下而得到的响应,用 来表示
电容放电的过程就是一个零输入响应,这个系统没有外部的输入,只有电容的初始储能,它按照指数规律逐渐衰减直至为零:

零输入响应对应的数学模型,按照定义,没有输入信号,所以所对应的微分方程就是等号右边为零:

齐次解的形式,常见的有这样三种:
- 第一种特征根是不等实根的情况,有n个不等的实根,那么齐次解的形式就是n个指数信号线性叠加;
- 第二种情况,特征根是相等的实根,齐次解的情况和不等实根略有不同,是k1倍的e的st次方加k2倍的t乘以e的st次方一直加加到Kn乘以e的n减1次方e的st次方;
- 第三种情况,特征根是成对的共轭复根,一共有二分之n对,齐次解的形式是实指数信号乘以括号余弦信号和正弦信号的线性叠加,一共有二分之n对。



下面看一道例题:

连续线性时不变系统的零状态响应
当系统的初始状态为零时,由系统的外部激励x(t)作用下产生的响应,称之为系统的零状态响应,用 来表示
在实际物理系统中,电容的充电过程就是一个零状态响应,前提条件是电容两端没有初始储能,完全由电压源来提供电荷;电容的充电过程是一个指数上升的过程:


求系统零状态响应的方法:
- 首先是经典法,就是直接求初始状态为零的非齐次方程,这个解包括齐次解和特解,经典法可以参阅吴大正先生的《信号与线性系统分析》这本教材;
- 第二种方法叫卷积法,又称之为卷积积分法,就是利用信号分解和线性时不变系统的特性来求解。
卷积法求系统的零状态响应的思路:
首先将任意信号分解为冲激信号的线性组合,然后求出冲激信号作用在系统上的零状态响应,称之为冲激响应,用h(t)来表示,第三,利用线性时不变特性,求出冲激信号的线性组合,也就是任意一个信号作用在系统的响应。

卷积积分法求解系统零状态响应的推导

连续时间线性时不变系统的冲激响应
冲激响应是指系统初始状态为零的条件下,以单位冲激信号激励系统产生的响应,用h(t)来表示。
简单地说,单位冲激响应就是单位冲激信号作用下的零状态响应。也就是说,从物理概念上来说冲激响应属于零状态响应
冲激响应对应的数学模型:

- 等号的左边就是冲激响应h(t)和它的各阶导数的线性叠加
- 等号的右边就是冲激信号δ(t)和它的各阶导数的线性叠加
冲激平衡法求系统的单位冲激响应

下面来看几道例题:

按照冲激响应的定义,把输入信号替换为δ(t),把响应y(t)替换为h(t)
显然动态方程的特征根S等于-4,而且n大于m,这里方程左边最高阶导数是1,所以n等于1,右边输入信号最高阶导数为0,所以m等于0,满足n大于m的条件。
所以按照前面给出的齐次解的形式的公式,我们可以确定单位冲激响应的形式,再把h(t)和它的一阶导数分别代入方程,便可以解出最终结果。
下面来看另一道例题:

依然是按照冲激响应的定义,把x(t)用δ(t)代替,y(t)用h(t)代替,得到一个新的微分方程。观察一下,等号两边最高阶导数的阶次,响应的最高阶导数是1,输入信号的最高阶导数也是1,也就是特征根S等于-4,m等于n。

下面来对比一下上面这两道例题:

下面是对冲激平衡法做的总结:

卷积积分

从卷积积分的定义我们可以看出,x(t)和h(t)相卷积,其实最终就是一个求积分的过程,但是其中包含了x(t)和h(t)的变量代换,按照公式,左边的x(t)变成x(τ),右边的h(t)变成h(t-τ),然后在一定的上下限范围内进行积分运算。
卷积积分的计算方法有多种,主要包括图解法、解析法、数值计算法和查表法。
图解法
具体步骤如下所示:

下面看几道例题:

分成5段进行分析:


综上可知:

也就是说,两个不等宽的矩形脉冲的卷积,为一个等腰梯形信号,卷积运算其实是一个变上限积分,两个信号卷积,卷积的结果仍然为一个信号,卷积最终得到的信号的起点,等于两个信号起点之和,终点等于两个信号的终点之和
解析法

下面来看几道例题:

首先画出u(τ)的波形,为了画出u(t-τ)的波形,或者说画出u(-τ+t)的波形,我们首先画出u(τ+t)的波形,t大于0,左加右减,在u(τ)的基础上向左平移t个单位;然后以纵轴为对称轴调转180度,就求得了u负(-τ+t),或者说画出u(t-τ)的波形。
用红线标识出u(τ)和u(t-τ)两个波形它们的公共的时间范围。两个函数不等于0的时间范围是0到t,所以u(t)卷积u(t)最终的积分时间范围上下限是0到t,在0到t的范围内函数值为1,最终积分结果是t。t乘以u(t)也就是斜坡信号r(t)。
再看看下面这道例题:

这里依然要注意变量为τ,与变量τ无关的e的负5t次方可以挪到积分符号以外,积分符号以内就是在u(τ)乘以u(t-τ)的范围内对一个指数信号e的2τ次方求积分。
总结一下就是:

连续时间LIT系统的零状态响应以及全响应分解
以一道例题讲解:

先来看第一部分:


首先根据冲激平衡法来判断冲激响应里面是否含有δ(t)或者它的高阶导数。
方程的右边只有一个δ(t),相应的方程的左边最高阶导也就是h"(t)对应的是δ(t)向右积分, h’(t)里面只有u(t)这样的形式,所以由此可以判断冲激响应h(t)里面也不会含有冲激信号δ(t)。
然后根据前边得出的特征根,两个不等的特征根,我们可以得出冲激响应的形式:A倍的u(t)加B倍的e的负2t次方u(t)。
冲激响应是在单位冲激信号作用下的零状态响应,生活中有很多例子是在某一个时间很短、幅值很大的一个信号作用下得到的。比如说,电闪雷鸣是模拟了冲激信号,啄木鸟通过敲击树洞听响声也是,判断树洞里边是空心的还是实心的;同样道理,在菜市场买西瓜其实也是求冲激响应,当然,给西瓜的不是幅值为无穷大的冲激信号,而是给了一个时间比较短、相对来说幅值比较大的一个信号来判断西瓜的成熟程度,这就是冲激响应。
 把输入信号二倍的e的负t次方u(t),和刚刚计算出的单位冲激响应:1减去e的负2t次方乘以u(t)进行卷积计算
把输入信号二倍的e的负t次方u(t),和刚刚计算出的单位冲激响应:1减去e的负2t次方乘以u(t)进行卷积计算

最后,把零输入响应和零状态响应两个表达式加在一起就是全响应。
下面对刚刚这道例题得出的解进行分解,也就是将全解分解或者说将全响应进行分解:


全响应除了可以分解为齐次解加特解、分解为固有响应和强迫响应之外,系统的全响应还可以分解为暂态响应加稳态响应:
- 稳态响应是完全响应中不随时间的增加而衰减的部分
- 暂态响应是完全响应中随着时间的增加很快衰减趋于零的部分
卷积的性质及奇异信号卷积
卷积的性质
 可以看出,卷积积分的这样三个交换律、分配律和结合律这个性质,和乘法的交换律、分配律、结合律非常的相似。
可以看出,卷积积分的这样三个交换律、分配律和结合律这个性质,和乘法的交换律、分配律、结合律非常的相似。

- 位移性质,已知x1(t)卷积x2(t)等于y(t),那么x1(t)向右平移t1再卷积x2(t)向右平移t2,卷积的结果是y(t)向右平移t1加t2,这是位移性质。
- 微分性质,已知x(t)和h(t)卷积,当然也满足交换律,那么y(t)的一阶导数就等于x(t)的一阶导数卷积h(t),或者等于x(t)卷积h(t)的一阶导数。

-
积分性质,也是已知y(t)等于x(t)和h(t)的卷积,那么y(t)的积分等于x(t)的积分卷积h(t),或者等于x(t)卷积h(t)的积分。
-
等效性质,仍然是已知x(t)和h(t)的卷积等于y(t),那么x(t)的积分卷积h(t)的一阶导数,就等于x(t)的导数卷积h(t)的积分。最终结果仍然等于y(t),这个就是等效性。
奇异信号的卷积
奇异信号卷积的性质和普通信号卷积性质类似,只是普通信号卷积性质的一个特例。

- 延迟特性,普通信号x(t)卷积冲激信号δ(t-t0),结果就等于x(t)平移,向右平移t0。同样的道理,普通信号x(t-t1)卷积δ(t-t2),结果就是x(t)向右平移t1加t2。
- 微分特性,x(t)卷积冲激偶信号,也就是x(t)卷积冲激信号的一阶导数,其结果就等于对x(t)求导。
- 积分特性,是用普通信号和阶跃信号卷积,其结果就是对该信号x(t)的变上限积分,或者说就是结果等于对x(t)的一次积分。
来看一下例题:
这道例题跟上面讲的例题是完全一样的,只不过在这里要利用平移特性计算这样两个矩形脉冲的卷积:

首先把x(t)和h(t)分别用阶跃信号表示,x(t)等于u(t)减u(t-1),h(t)等于u(t)减u(t-2)。
首先要用到分配律将 u(t)-u(t-1) 和 u(t)-u(t-2) 进行分别卷积
然后利用平移特性来计算最终的结果,按照这道题的已知条件,u(t)卷积u(t)等于r(t),也就是阶跃信号和自身卷积等于斜坡信号,那么后面的u(t-1)卷积u(t),就是r(t)向右平移一个单位;依此类推,后边第三项和第四项也可以用平移特性。

两个信号进行卷积的结果,图像也是一个梯形脉冲。
再来看一道例题:

首先我们对左边的x(t)求它的一阶导数,这是一个矩形脉冲,在t等于0时刻和t等于1时刻,分别有向上的跳跃和向下的跳跃,所以一阶导数就是δ(t)减δ(t-1)。然后我们利用微分性质,y(t)的一阶导数等于x(t)一阶导数卷积h(t),也就是用δ(t)减δ(t-1)卷积h(t),那么结果就是h(t)再减h(t-1)。这是利用微分性质。
最后由一阶导数倒过来积分运算,得到原函数y(t),也就是对h(t)减h(t-1)进行变上限积分,那y(t)的一阶导数、波形,如右图所示,对它进行积分,阶跃信号积分得斜坡信号,就可以得到右下角的波形,就是最终的要求计算的x(t)和h(t)的卷积积分。
3. 离散时间LTI系统的响应

比较线性系统和离散系统

离散LTI系统的零输入响应
离散系统的零输入响应概念和连续系统是相同的

离散系统零输入响应(齐次解)的形式
 下面看一个求解离散系统零输入响应的例题:
下面看一个求解离散系统零输入响应的例题:


离散LTI系统的单位脉冲响应
- 系统的零状态响应:
当系统的初始状态为零时, 由系统的外部激励x[k]产生的响应称为零状态响应,用 表示。

卷积法求解系统零状态响应
推导:

离散系统的单位脉冲响应
单位脉冲序列δ [k]作用于离散时间LTI系统所产生的零状态响应称为单位脉冲响应,用符号h[k]表示。

求解方法:
- 迭代法
- “脉冲函数平衡法” +齐次解形式
下面看一道具体的例题:



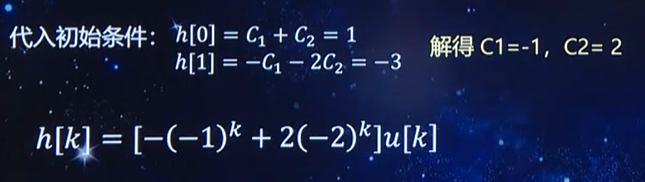
再来看另一道例题:



卷积和法求离散系统零状态响应
序列的卷积和常用的求解方法包括图解法、列表法和解析法。这里主要讲列表法和解析法。
列表法
列表法计算序列卷积和,进而用卷积和法求离散系统零状态响应:

以上求解过程可以归纳成列表法。

下面看一道例题:

把x[k]写成一行,把h[k]写成一列。彼此相对应的各个交差点相乘,然后画一个对角线,画上每一处的对角线,把对角线的各个数值相加,最终得到卷积和的结果
x[k]这个信号的起点是k等于2时刻,h[k]的起点是k等于1时刻,两者相加,最终卷积和y[k]的起点就是k等于3时刻
下面是解法二:

不管是列表法还是竖式乘法,这两种方法都适用于两个序列是有限长序列的情况,否则的话最终求的结果是无穷无尽的。
再来看一道综合性的例题:




接下来再看一道例题:

这道例题是在前一个例题的基础上,要求求出系统的固有响应和强迫响应,以及瞬态响应和稳态响应:


冲激响应表示的系统特性
冲激响应表示的系统特性包含这样四个部分,分别是:连续系统的级联和并联,以及离散系统的级联和并联。
冲激响应表示的系统特性

可以看出,响应曲线是不相同的,也就是说系统不同,它的冲激响应h(t)也不相同。那么,利用冲激响应就可以表示系统的时域特性。
级联系统的冲激响应

并联系统的冲激响应

单位脉冲响应表示的系统特性

级联系统的脉冲响应

并联系统的脉冲响应
