信号的时域分析

信号的时域分析

0.前言

主要内容为：基本信号，基本运算，基本分解

代码演示图像参考

一.连续时间基本信号

1.普通信号

（一）指数类信号

$f(t)=K\,e^{\sigma t +j\omega t } \begin{cases} 直流信号\quad f(t)=K &\sigma=0, \omega=0 \\ 实指数信号 \ f(t)=K\,e^{\sigma t } & \sigma\neq0, \omega=0 \\ 等幅振荡正弦信号\ f(t)=K\,e^{ j\omega t}& \sigma=0, \omega\neq0 \\ 不等幅振荡正弦信号 \ f(t)=K\,e^{\sigma t+j\omega t }& \sigma\neq0, \omega \neq0 \end{cases}$

$其中 -∞ < t < +∞，K 为振幅$

其中 -∞ < t < +∞，K 为振幅， $\omega为角频率$

（1）直流信号

$f(t)=K$

（2）实指数信号

$f(t)=K\,e^{\sigma t}$

• $\sigma$是决定信号幅度随时间增长或衰减的因子。

• $\tau= \frac {1}{|\,\sigma \,|}$ ,称为实指数信号的时间常数。

  当 $t= \tau$ 时， $f(\tau)= K e^{-1}=0.368K$ ,表示实指数信号衰减为初始值的36.8%

（3）等幅振荡正弦信号

$f(t)=K \, e^{ j \omega t}$

由 Euler 得
$f（t）=Ke^{j\omega t}=Kcos \omega t+jKsin\omega t$

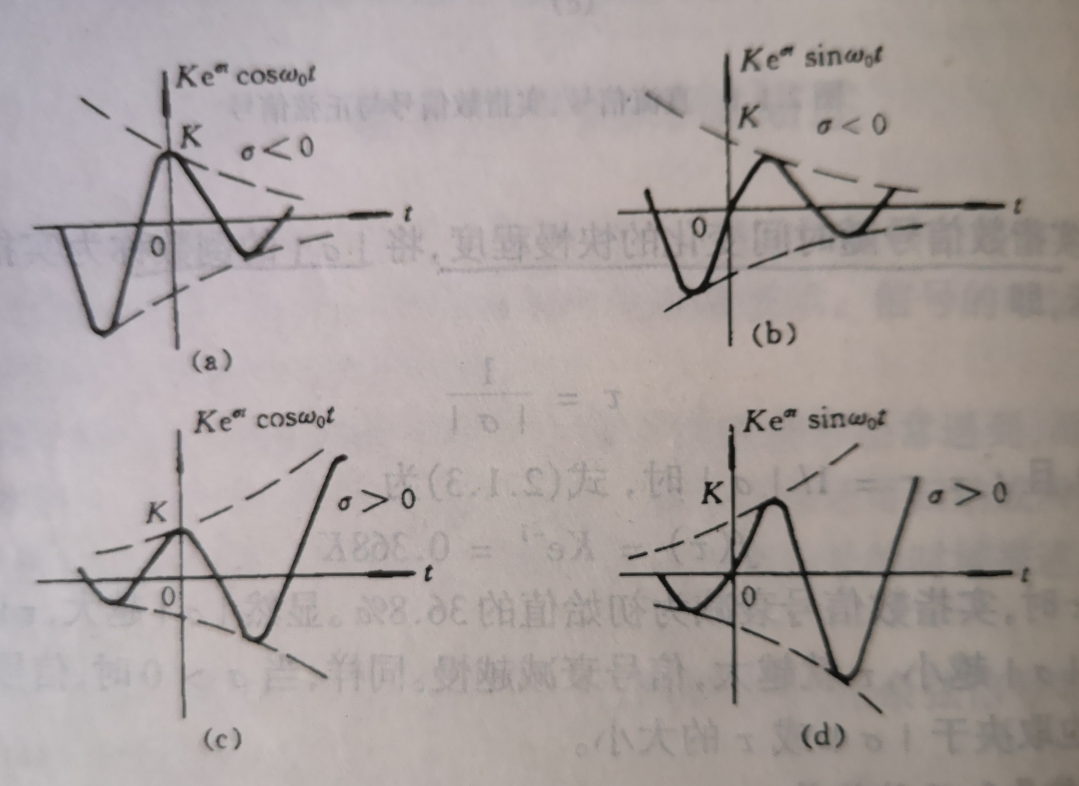
（4）不等幅振荡正弦信号

$f(t)=K\,e^{\sigma t+j\omega t}$

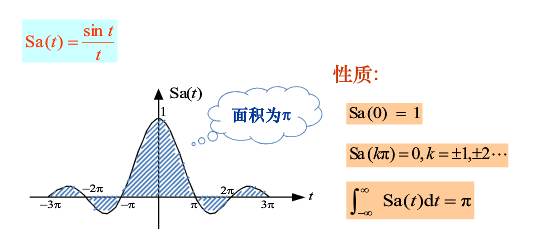
(二)取样信号

2.奇异信号

特征：数学表达式属于奇异函数，即在函数本身或其导数或高阶导数具有不连续点（跳变点）。

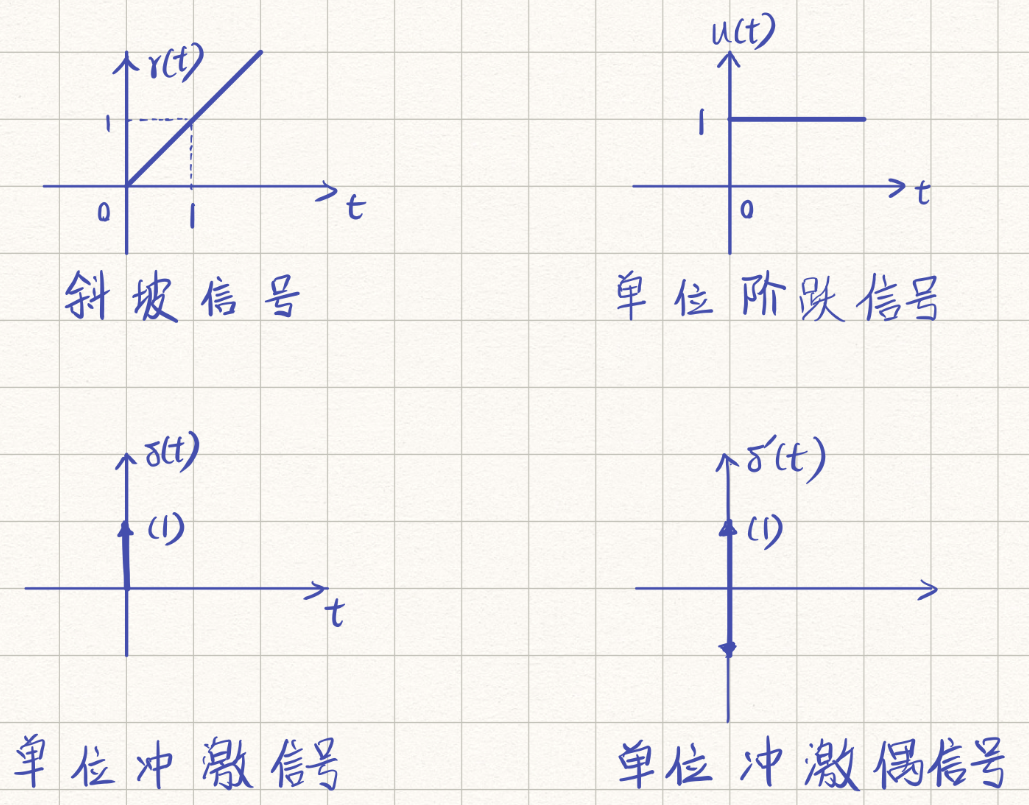
（1）斜坡信号 $\quad r（t)$

$r(t)= \begin{cases} t & t>0 \\ 0& t<0 \end{cases}$

（2）单位阶跃信号 $u(t)$

$u(t) = \begin{cases} 1 & t>0 \\ 0& t<0 \end{cases}$

作用：A. 阶跃信号可以表示任意矩形脉冲信号

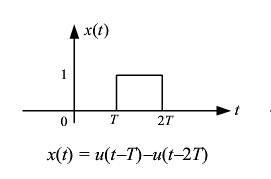
​ B.利用阶跃信号的单边性表示信号的时间范围
$例：\quad sin\ wt·u(t-t_0) = \begin{cases} sin\ wt & t>t_0 \\ 0& t<=t_0 \end{cases}$

（3）单位冲激信号 $\delta(t)$

$\delta (t) = \begin{cases} 0 & t\neq 0 \\ \rightarrow ∞& t=0 \end{cases}$

也可以运用泛函数 表示，$ \phi (t) 为任意一个在t=0处连续的普通函数 $
$\begin{aligned} \int_{-∞}^{∞} \delta(t) ·\phi(t) \mathrm{d} t=\phi(0) \end{aligned}$
性质：

A.筛选特性

$x(t)\delta(t-t_0)\ = x(t_0)\delta(t-t_0)$

B.抽样特性

$\begin{aligned} \int_{-∞}^{∞} \delta(t-t_0) ·\phi(t) \mathrm{d} t=\phi(t_0) \end{aligned}$

C.展缩特性

$\delta(at)=\frac{1}{|a|}\delta(t)$

D.卷积特性

（4）单位冲激偶信号 $\delta’(t)$

$\delta’(t)=\frac{d\delta(t)}{dt}$