前言
汇总版在这篇文章:自动控制原理上课笔记
线性系统的根轨迹法
根轨迹简称根迹,它是开环系统某一参数从0变到 ∞ \infty ∞ 时,闭环系统特征方程式的根在 s 平面上变化的轨迹。
根轨迹的分类:180度根轨迹 、参数根轨迹、零度根轨迹、根轨迹簇。
当闭环系统没有零点与极点相消时,闭环特征方程式的根就是闭环传递函数的极点,我们常简称为闭环极点。
从已知的开环零、极点位置及某一变化的参数来求取闭环极点的分布,实际上就是解决闭环特征方程式的求根问题。
因为系统的稳定性由系统闭环极点唯一确定,而系统的稳态性能和动态性能又与闭环零、极点在 s 平面上的位置密切相关,所以根轨迹图不仅可以直接给出闭环系统时间响应的全部信息,而且可以指明开环零、极点应该怎样变化才能满足给定的闭环系统的性能指标要求。
根轨迹法应用前提条件是受控系统的传递函数没有零极点相消。
- 闭环系统根轨迹增益,等于开环系统前向通路根轨迹增益。对于单位反馈系统,闭环系统根轨迹增益就等于开环系统根轨迹增益。
- 闭环零点由开环前向通路传递函数的零点和反馈通路传递函数的极点所组成。对于单位反馈系统,闭环零点就是开环零点。
- 闭环极点与开环零点、开环极点以及开环根轨迹增益均有关。
根轨迹是系统所有闭环极点的集合:
根轨迹方程 K ∗ ∏ j = 1 m ( s − z j ) ∏ i = 1 n ( s − p i ) = − 1 \text{根轨迹方程 }K^*\frac{\prod_{j=1}^{m}(s-z_j)}{\prod_{i=1}^{n}(s-p_i)}=-1 根轨迹方程 K∗∏i=1n(s−pi)∏j=1m(s−zj)=−1
模值条件:
K ∗ = ∏ i = 1 n ∣ s − p i ∣ ∏ j = 1 m ∣ s − z j ∣ K^*=\frac{\prod_{i=1}^{n}|s-p_i|}{\prod_{j=1}^{m}|s-z_j|} K∗=∏j=1m∣s−zj∣∏i=1n∣s−pi∣
相角条件:180度相角差
性质
- 由于闭环特征方程中的某些系数是根轨迹增益 K ∗ K^* K∗ 的函数,所以当 K ∗ K^* K∗ 从零到无穷大连续变化时,特征方程的某些系数也随之而连续变化,因而特征方程式根的变化也必然是连续的,故根轨迹具有连续性。
- 根轨迹必对称于实轴的原因是显然的,因为闭环特征方程式的根只有实根和复根两种,实根位于实轴上,复根必共轭,而根轨迹是根的集合,因此根轨迹对称于实轴。
- 根据对称性,只需做出上半 s 平面的根轨迹部分,然后利对称关系就可以画出下半 s 平面的根轨迹部分。
分离点
- 一般情况下,常见的根轨迹分离点是位于实轴上的两条根轨迹分支的分离点。
- 如果根轨迹位于实轴上两个相邻的开环极点之间,其中一个可以是无限极点,则在这两个极点之间至少存在一个分离点。
- 同样,如果根轨迹位于实轴上两个相邻的开环零点之间,其中一个可以是无限零点,则在这两个零点之间也至少有一个分离点。
180度根轨迹绘制法则
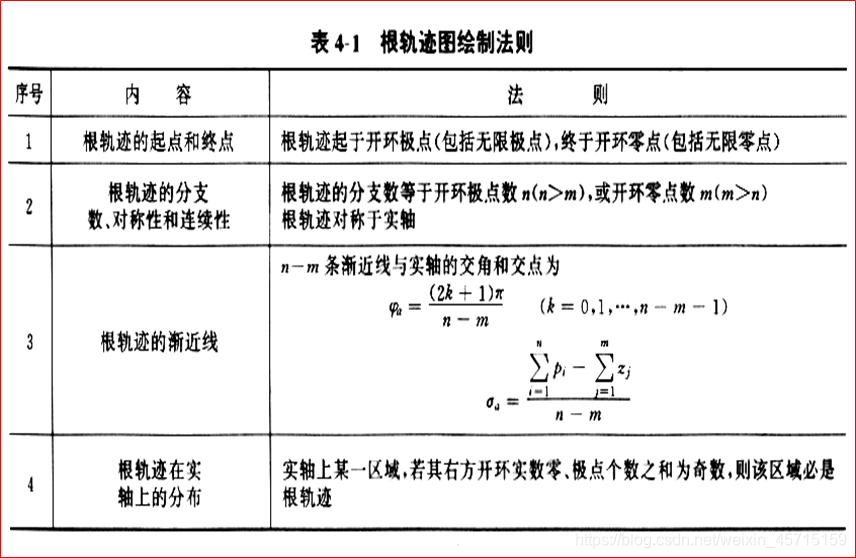
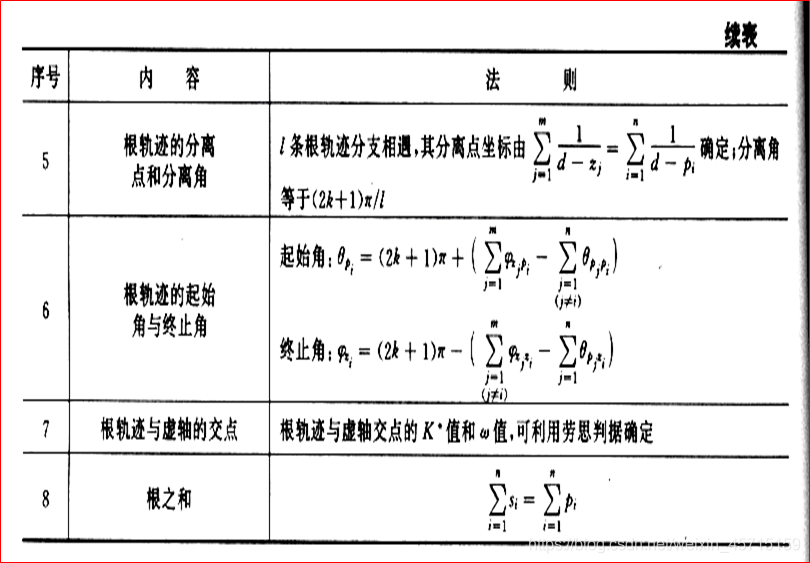
对于特定 K ∗ K^* K∗ 值下的闭环极点,可用模值条件确定。
在控制系统中,除根轨迹增益 K ∗ K^* K∗ 以外,其他情形下的根轨迹统称为广义根轨迹。包括:
- 参数根轨迹
- 零度根轨迹
- 非最小相位系统根轨迹
通常,将负反馈系统中 K ∗ K^* K∗ 由零变到无穷大时的根轨迹叫做常规根轨迹(或180度根轨迹)。
以非开环增益/根轨迹增益为可变参数绘制的根轨迹称为参数根轨迹,以区别于以开环增益 K K K /根轨迹增益 K ∗ K^* K∗ 为可变参数的常规根轨迹。
一般说来,零度根轨迹的来源有两个方面:
- 是非最小相位系统中包含 s 最高次幂的系数为负的因子。
- 是控制系统中包含有正反馈内回路。
零度根轨迹绘制法则
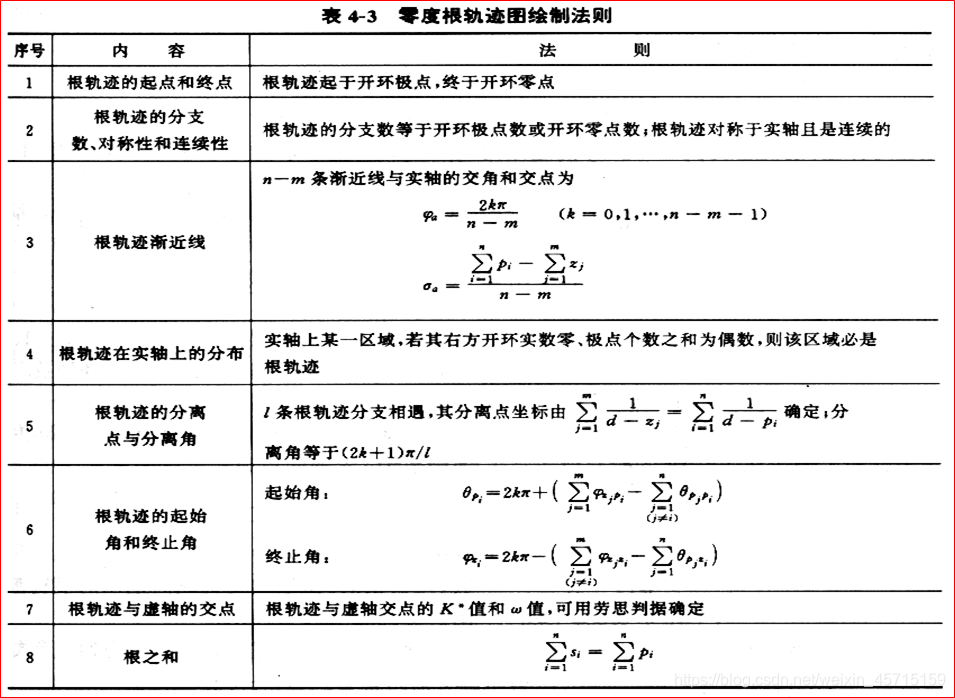
如果系统的所有开环极点和零点都位于s平面的左半平面,则称为最小相位系统。
若系统的开环传递函数在右半 s 平面有零点或极点,则该系统称为非最小相位系统:
- 正反馈系统
- 具有正反馈性质的系统
- 具有右半s平面极零点
闭环零点的影响
闭环零点对系统动态性能的影响,相当于减小闭环系统的阻尼,从而使系统的过渡过程有出现超调的趋势,并且这种作用将随闭环零点接近坐标原点的程度而加强。
在开环系统中增加极点,会使根轨迹向右移动,从而降低系统的相对稳定性,增加系统响应的调节时间。
如果闭环零、极点相距很近,那么这样的闭环零、极点常称为偶极子。偶极子有实数偶极子和复数偶极子之分,而复数偶极子必共轭出现。不难看出,只要偶极子不十分接近坐标原点,它们对系统动态性能的影响就甚微,从而可以忽略它们的存在。
闭环零点的存在,将使系统的峰值时间提前,这相当于减小闭环系统的阻尼,从而使超调量加大,当闭环零点接近坐标原点时,这种作用尤甚。
一般说来,闭环零点对调节时间的影响是不定的。
闭环实数主导极点对系统性能的影响是:闭环实数主导极点的作用,相当于增大系统的阻尼,使峰值时间迟后,超调量下降。
如果实数极点比共轭复数极点更接近坐标原点,甚至可以使振荡过程变为非振荡过程。