视觉SLAM学习笔记

本文是个人对《视觉SLAM十四讲》的内容进行个人理解说写下的笔记以备忘

第三讲

向量
向量一般为列向量,用小写字母表示。
向量相乘
点乘为内积，可表达为以下，<a,b>为向量a、b间夹角，结果可描述为向量间投影关系。

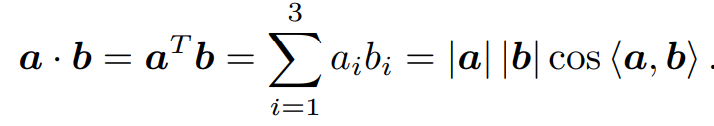
叉乘为外积，可表达如下，结果为列向量，同时该列向量垂直于向量a、b，为两个向量张成的四边形有向面积。

而在上述的运算中可知，向量a等价于反对称矩阵，如下，既向量转换为矩阵的一个重要的变换，用a^表示。反对称矩阵A有以下变换AT=-A。
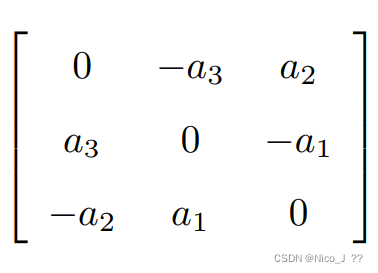
坐标
向量a(a1,a2,a3)T在基(e1,e2,e3)下，坐标为a1e1+2e2+a3e3，表达式如下。

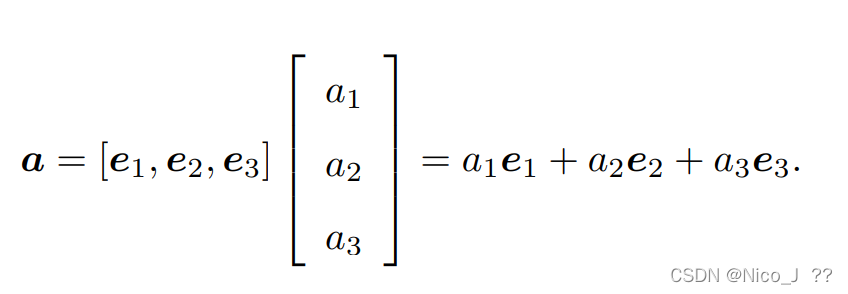
经过旋转，向量于基均发生改变，表达式如下

化简，得到旋转矩阵R，如下。
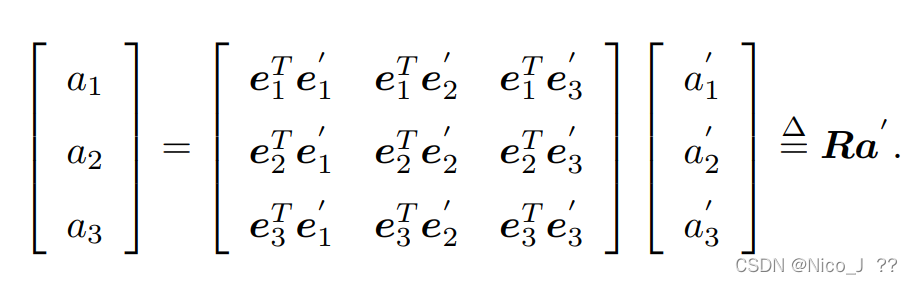
旋转矩阵
对于旋转矩阵R，定义李群SO(3)，如下。det()为计算行列式

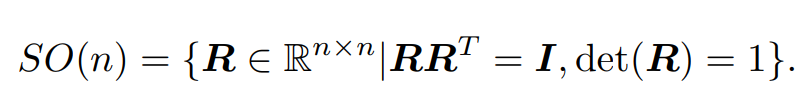
对于反向旋转可

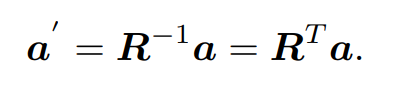
考虑到平移，需加上平移向量t，其中T为变换矩阵四维。

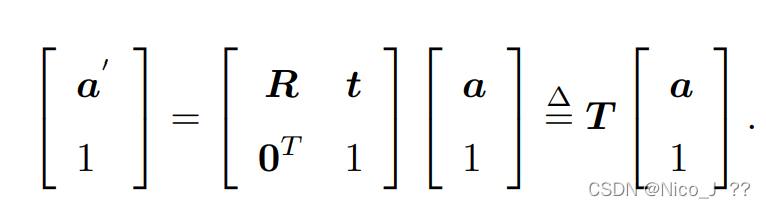
于是有定义李群SE(3)，如下。

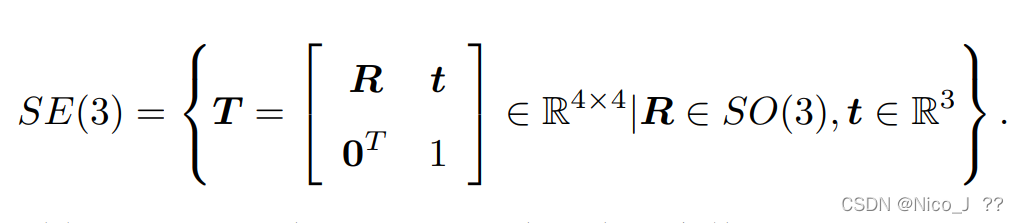
变换矩阵T的逆表示维。

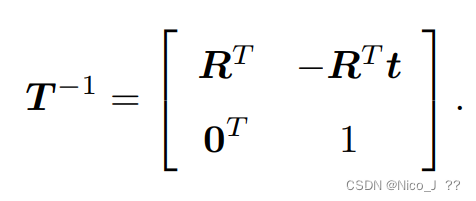
对于安装完成Eigen后编译索引失败，需运行以下命令复制文件夹。
```
sudo cp -r /usr/local/include/eigen3/Eigen /usr/local/include
```
旋转向量
旋转矩阵必须是一个正交矩阵且行列式需为1，变换矩阵也是如此，这些约束使得求解变得困难，考虑到数据的紧凑性，为此定义旋转向量。
任意旋转可用一旋转轴与旋转角刻画，用一单位向量表示旋转轴，其长度表示旋转角，单位为rad。有罗德里格斯公式，如下。

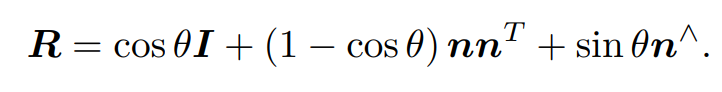
计算R的迹有

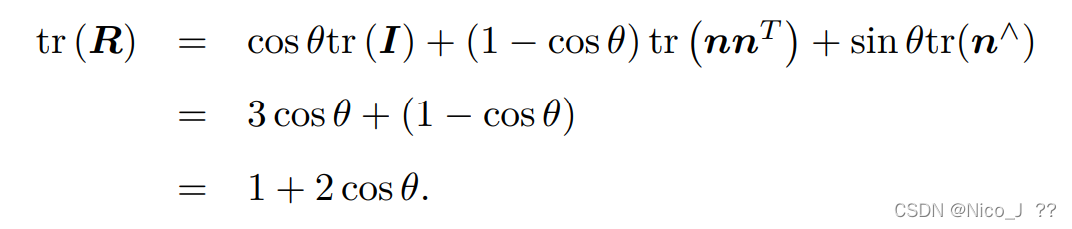
故旋转角

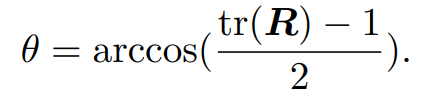
对于旋转轴n的旋转为：Rn=n
欧拉角
绕Z轴旋转-偏航-yaw
绕Y轴旋转-俯仰-pitch
绕X轴旋转-滚转-roll
故可以[r, p, y]T 三维的向量描述旋转，不过注意旋转顺序之分。
关于万象锁的问题，简单来说对三轴的旋转过程中，第二次旋转为90°时，会出现第一次的旋转轴与第三次旋转轴相同。
四元数
四元数由一个实部和三个虚部组成

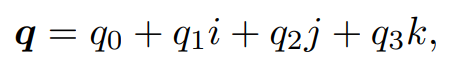
有以下关系

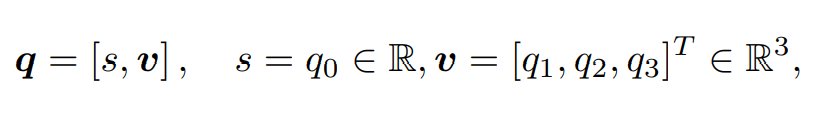
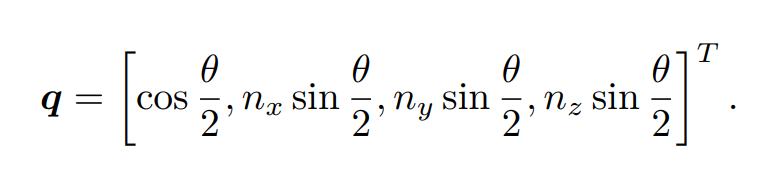
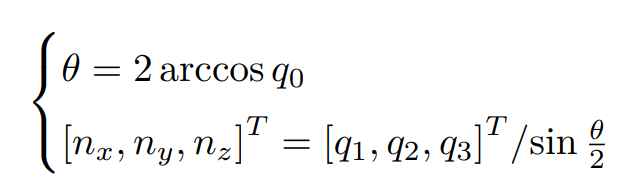
第四讲

李群
旋转矩阵与变换矩阵分别构成特殊正交群SO(3)、特殊欧氏群SE(3)，如下

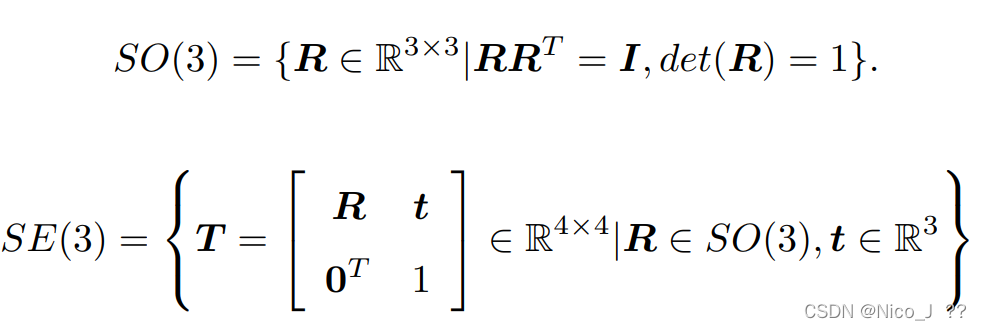
对于群是一种集合加上一种运算的数据结构。满足以下条件，简称封结幺逆
封闭性: ∀a1, a2 ∈ A, a1 · a2 ∈ A.
结合律: ∀a1, a2, a3 ∈ A, (a1 · a2) · a3 = a1 · (a2 · a3).
幺元: ∃a0 ∈ A, s.t. ∀a ∈ A, a0 · a = a · a0 = a.
逆: ∀a ∈ A, ∃a−1 ∈ A, s.t. a · a−1 = a0.

关于旋转矩阵满足 RRT=I
求导化简得

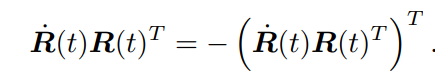
得知为反对称矩阵
回忆反对称矩阵，如下，^为向量转换为矩阵，而∨为矩阵转换为向量

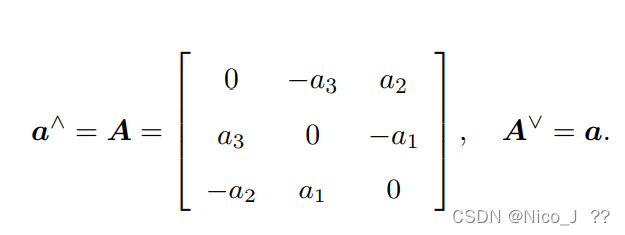
于是对R(t)R(t)T = ϕ(t)∧化简得同时得知对旋转矩阵求导只需左乘一个反对称矩阵即可
ϕ 反映了 R 的导数性质，故称它在 SO(3) 原点附近的正切空间

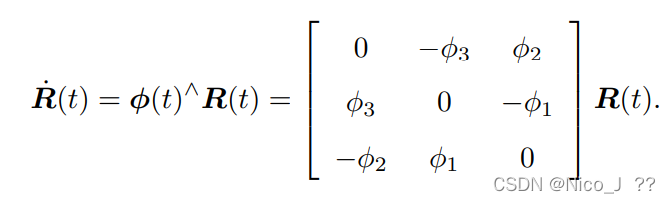
一阶泰勒展开为 f(x)=f(x0)+f’(x0)(x-x0)+o(x-x0) o为极小量
f(x)≈f(x0)+f’(x0)(x-x0)
于是

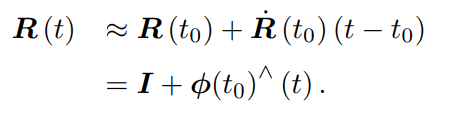
注意这里，R(t)与0处一介泰勒展开后，近似认为R(t)为t的一介函数，而ϕ(0)^为正切，即斜率。
R(t)=I+ϕ(0)^ * t
微分有 dR(t)=ϕ(0)^ … … …(1)
而求导公式为R(t)‘=ϕ(t)^ * R(t) … … … .(2)
理解一下(1)和(2)
R(t)’=ϕ(0)^ * R(t) … … …强行解释为用斜率ϕ(0)^ 替代ϕ(t)^ ???还是不太理解
求积分得到
R(t)=e^(ϕ(0)t)

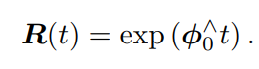
在这里插入图片描述
存在一个问题，根据上述及书上公式化简，普遍存在 R=exp(ϕ△)=I+ϕ△，那我们计算这个行列式会发现det®=1+a1²+a2²+a³≠1，那这也反映了这个约等于的误差

李代数
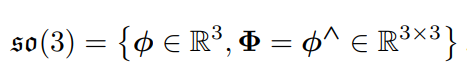
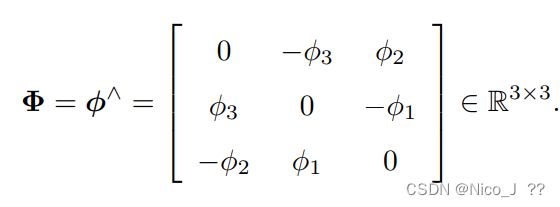
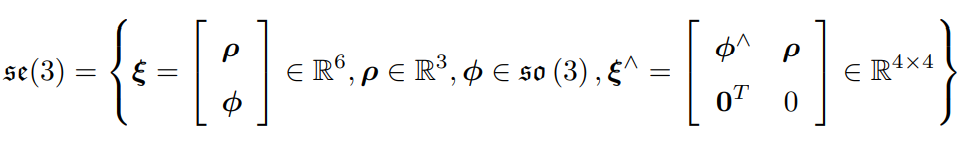
指数与对数映射
SO(3)指数与对数映射
ϕ 是三维向量等价于ϕ^这个反对称矩阵，而这个反对称矩阵在允许误差范围加一个I则表示为旋转矩阵，现在用ϕ既然是三维向量，尝试定义这个向量的模长和方向，分别记作 θ 和 a，于是有 ϕ = θa。这里 a 是一个长度为 1 的方向向量，满足以下两个性质。
a∧a∧ = aaT − I,
a∧a∧a∧ = −a∧

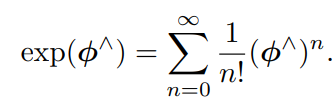
然后进行推导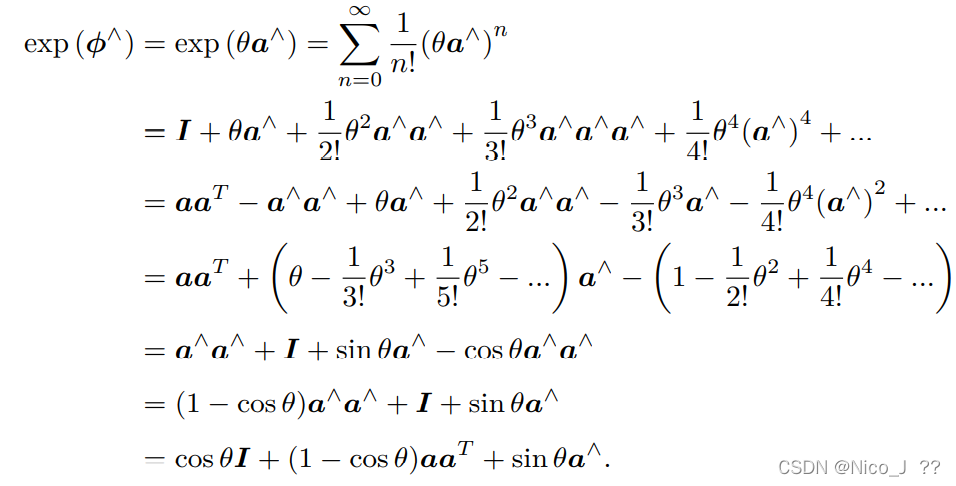
发现这个推导的结果与旋转向量的罗德里格斯公式相同，那么得到一个重要的推断，反对称矩阵对应的向量就算旋转向量，既ϕ就是一个旋转向量，既李代数so(3)就是旋转向量！！！！！！
那旋转向量可由对数映射得到，既如下等式

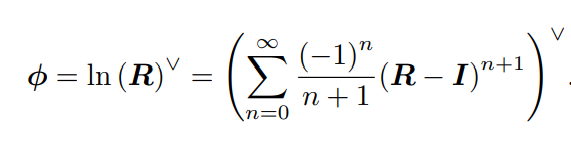
SE(3)指数与对数映射

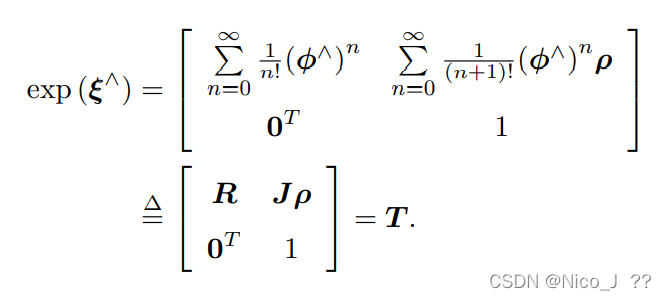
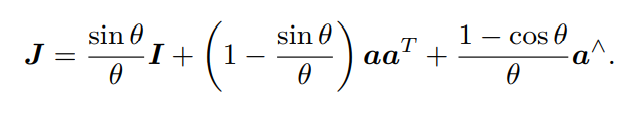
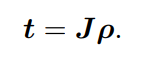
于是大总结
李代数求导与扰动模型
两个李代数指数映射乘积的完整形式，由 Baker-Campbell-Hausdorff 公式（BCH 公
式）得到

当 ϕ1 或ϕ2 为小量时，小量二次以上的项都可以被忽略掉。此时，BCH 拥有线性近似表达为

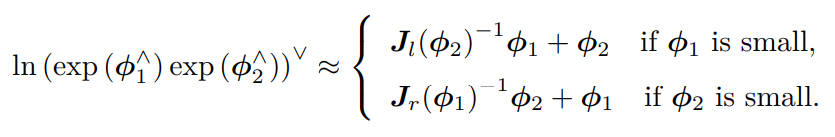
左乘 BCH 近似雅可比 Jl如下

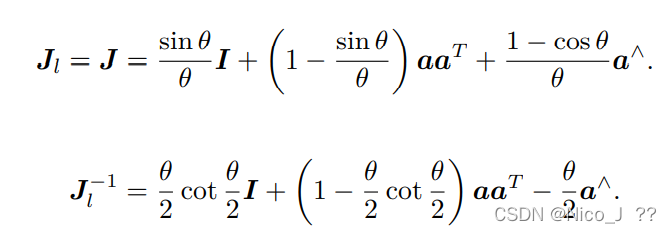
左乘 BCH 近似雅可比 Jl

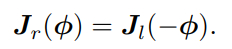
假定对某个旋转 R，对应的李代数为 ϕ。我们给它左乘一个微小旋转，记作 ∆R，对应的李代数为 ∆ϕ。那么，在李群上，得到的结果就是 ∆R · R，而在李代数上，根据 BCH近似，为：J⁻¹(ϕ)∆ϕ + ϕ。合并起来，可以简单地写成

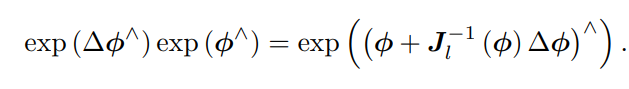
反之，如果我们在李代数上进行加法，让一个 ϕ 加上 ∆ϕ，那么可以近似为李群上带
左右雅可比的乘法：

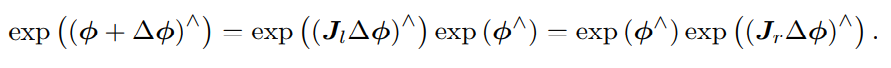
同样的对于SE(3)，有如下

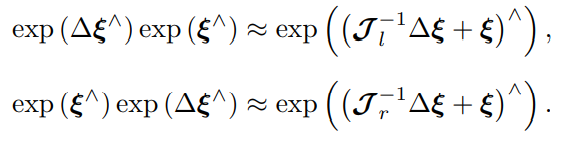
于是有有一点点点点点点点点点点点点点点点看不懂了
存在一点，坐标为p，相机位姿为T，对该点进行观测，得到贯彻数据z，噪声为w如下
z = T p + w.
那么实际数据与观测数据的误差e
e=z-Tp
如果存在一系列的点与观察那么需要寻找一个合适的T，以使整体误差最小

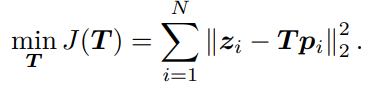
求解此问题，需要计算目标函数 J 关于变换矩阵 T 的导数。我们经常会构建与位姿有关的函数，然后讨论该函数关于
位姿的导数，以调整当前的估计值。然而，SO(3), SE(3) 上并没有良好定义的加法，它们
只是群。如果我们把 T 当成一个普通矩阵来处理优化，那就必须对它加以约束。而从李代
数角度来说，由于李代数由向量组成，具有良好的加法运算。因此，使用李代数解决求导
问题的思路分为两种：
1.用李代数表示姿态，然后对根据李代数加法来对李代数求导。
2.对李群左乘或右乘微小扰动，然后对该扰动求导，称为左扰动和右扰动模型。
1.李代数求导

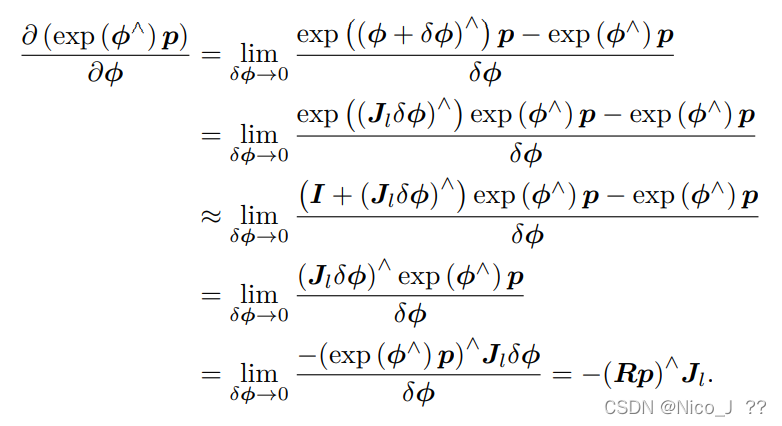
求导结果得到较复杂的 Jl
2.扰动模型
另一种求导方式，是对 R 进行一次扰动 ∆R。这个扰动可以乘在左边也可以乘在右
边，最后结果会有一点儿微小的差异，以左扰动为例

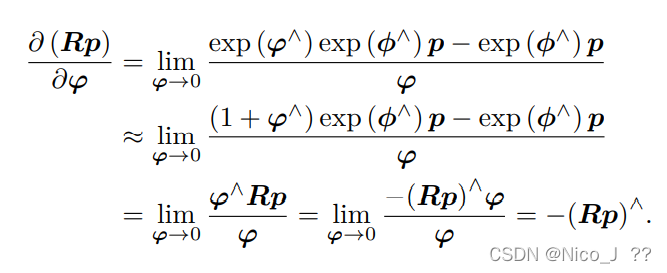
其实发现这两种方法的差别为右乘的一个Jl
于是对SE(3)进行求导，用扰动模型

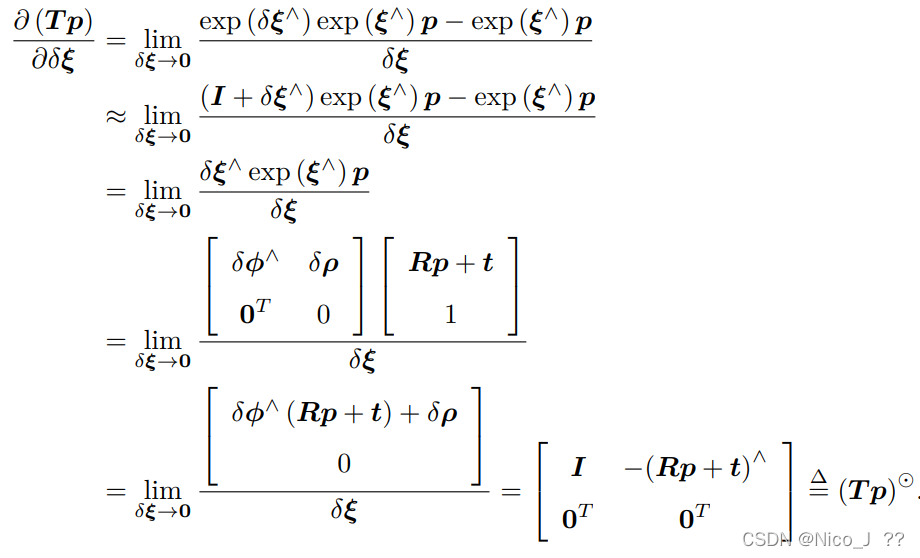
第五讲

相机模型
空间点P 的坐标为 [X, Y, Z]T，成像点P′ 为 [X′, Y ′, Z′]T

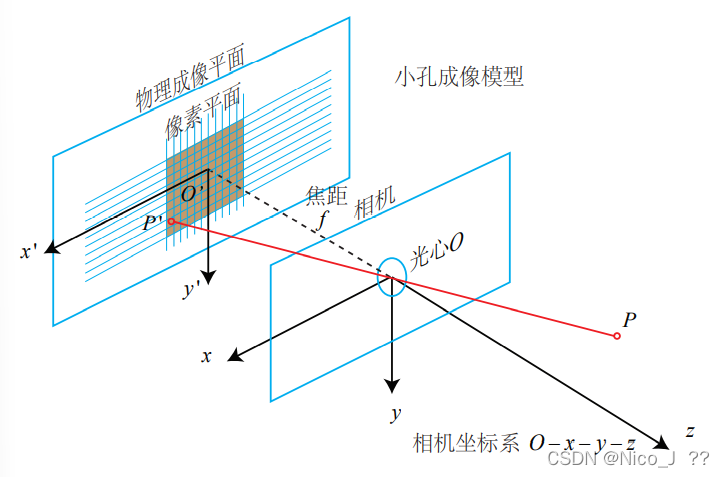
有三角关系，因成象是倒立的，所以有负号。

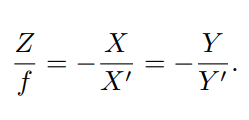
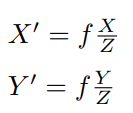
定义像素坐标系定义为原点 o′ 位于图像的左上角，u 轴向右与 x 轴平行，v轴向下与 y 轴平行。像素坐标系与成像平面之间，相差了一个缩放和一个原点的平移。设像素坐标在 u 轴上缩放了 α 倍，在 v 上缩放了 β 倍，同时这样优化了图像处理，使坐标系相同。因为原点平移了[cx,cy]T，P′ 的坐标与像素坐标 [u, v]T 的关系为，并把 αf 合并成 fx，把 βf 合并成 fy，如下

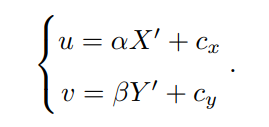
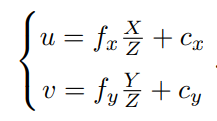
其中，f 的单位为米，α, β 的单位为像素每米，所以 fx, fy 的单位为像素，转化为矩阵，其中K命名为内参数矩阵。如下：

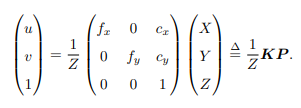
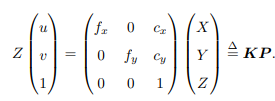
其中K命名为内参数矩阵,P为在相机坐标系下的坐标，由于P的相机坐标应该是世界坐标Pw，那相机的位姿由旋转矩阵R和平移向量t描述，那么

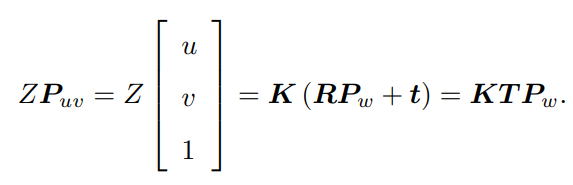
上式两侧都是齐次坐标。因为齐次坐标乘上非零常数后表达同样的含义，所以可以简
单地把 Z 去掉，如下：

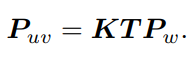
但这样等号意义就变了，成为在齐次坐标下相等的概念，相差了一个非零常数。对于归一化处理，既对最后一维赋值为1， Pc 可以看成一个二维的齐次坐标，称为归一化坐标。
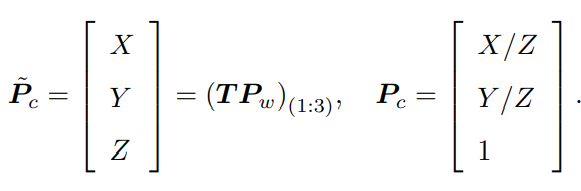
相机畸变
简单来说，径向畸变因为透镜形状发生改变而产生的畸变，导致图像中直线变曲线。切向畸变为透镜和成像面不平行也会引入切向畸变。
任意一点 p 可以用笛卡尔坐标表示为 [x, y]T, 也可以把它写成极坐标的形式[r, θ]T，其中 r 表示点 p 离坐标系原点的距离，θ 表示和水平轴的夹角。径向畸变可看成坐标点沿着长度方向发生了变化 δr, 也就是其距离原点的长度发生了变化。切向畸变可以看成坐标点沿着切线方向发生了变化，也就是水平夹角发生了变化 δθ。
对于径向畸变，无论是桶形畸变还是枕形畸变，由于它们都是随着离中心的距离增加
而增加。我们可以用一个多项式函数来描述畸变前后的坐标变化：这类畸变可以用和距中
心距离有关的二次及高次多项式函数进行纠正，其中 [x, y]T 是未纠正的点的坐标，[xcorrected, ycorrected]T 是纠正后的点的坐标，注意它们都是归一化平面上的点，而不是像素平面上的点。如下：

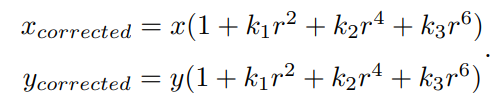
对于切向畸变，可以使用另外的两个参数 p1, p2 来进行纠正：

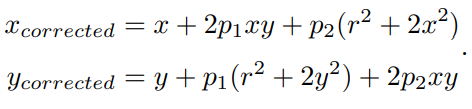
第六讲非线性优化

先验、后验、似然
以下为相机的一状态方程和一观测方程，其中xk为当前相机位姿，xk-1为上一刻相机位姿，uk为运动输入，wk为噪声，设定为符合正态分布。zk,j为在位姿xk处对路标yi观察得到的像素位置，yj为路标，xk为相机位姿，vkj为噪声，符合正态分布。

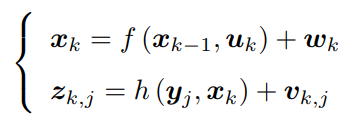
其中K 为相机内参，s 为像素点的距离，严格来说相机的观测方程可以表达为：

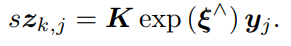
机器人状态的估计，是求已知输入数据 u 和观测数据 z 的条件下，计算状态 x 的条件概率分布

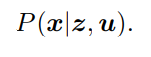
只有一张张的图像时，即只考虑观测方程带来的数据时，相当于估计 P(x|z) 的条件概率
分布。简单来说是根据照片对路标j的观察推断位姿x的可能性。该问题也称为 Structure from Motion（SfM），即如何从许多图像中重建三维空间结构。在这种情况下，SLAM 可以看作是图像具有时间先后顺序的，需要实时求解一个 SfM 问题。为了估计状态变量的条件分布，利用贝叶斯法则，贝叶斯法则的分母部分与待估计的状态 x 无关，因而可以忽略，简单来说就是P(x|z)正比于P(z|x) 与P(x)的乘积，求解最大后验概率，相当于最大化似然和先验的乘积。

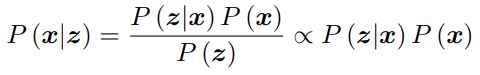
左侧通常称为后验概率，右侧的 P(z|x) 称为似然，P(x) 称为先验。直接求后验分布是困难的，但是求一个状态最优估计，使得在该状态下，后验概率最大化（Maximize a Posterior，MAP），则是可行的： arg max P(x|z)的意思是当P(x|z)最大时，变量的取值

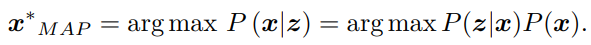
现在，在只有图像数据且无位置信息时，那么就没有了先验P(x)，那么求解x的最大大似然估计（Maximize Likelihood Estimation, MLE）：

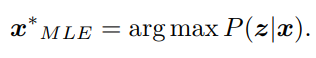
那么这个的意思可以理解为：观察的数据在最可能的位置姿态。
最小二乘
观测方程如下：

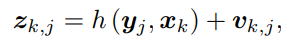
假设噪声项 vk ∼ N (0, Qk,j )，所以观测数据的条件概率为：

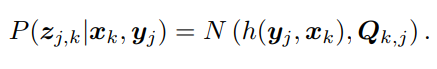
代入后依然符合高斯分布，为了计算使它最大化的 xk, yj，我们往往使用最小化负对数的方式，来求一个高斯分布的最大似然。
对于高维高斯分布 x ∼ N(µ, Σ)，概率密度函数展开形式为，并取负对数：

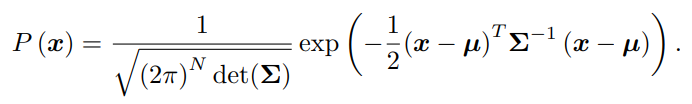
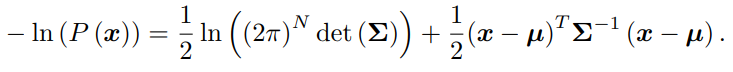
对原分布求最大化相当于对负对数求最小化。在最小化上式的 x 时，第一项与 x 无关，可以略去。于是，只要最小化右侧的二次型项，就得到了对状态的最大似然估计。简单来说：求最大化的P(x)，等价于求最小化的负对数，化简后，第一项与x无关，略去，于是只需最小化第二项，就可以得到对状态的最大似然估计，代入SLAM的观测模型，相当于求：

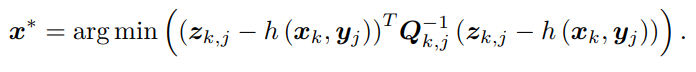
该式等价于最小化噪声项（即误差）的平方（Σ 范数意义下）。因此，对于所有的运动和任意的观测，我们定义数据与估计值之间的误差：

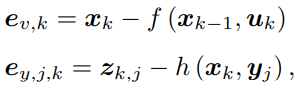
并求其误差的平方和

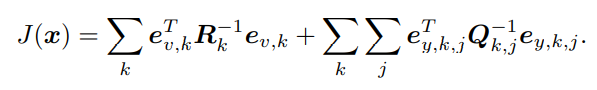
这就得到了一个总体意义下的最小二乘问题（Least Square Problem）。我们明白它的最优
解等价于状态的最大似然估计。直观来讲，由于噪声的存在，存在误差，为此，把状态的估计值进行微调，使得整体的误差下降一些。当然这个下降也有限度，它一般会到达一个极小值。这就是一个典型非线性优化的过程。
• 首先，整个问题的目标函数由许多个误差的（加权的）平方和组成。虽然总体的状
态变量维数很高，但每个误差项都是简单的，仅与一两个状态变量有关。例如运动
误差只与 xk−1, xk 有关，观测误差只与 xk, yj 有关。每个误差项是一个小规模的约
束，我们之后会谈论如何对它们进行线性近似，最后再把这个误差项的小雅可比矩阵
块放到整体的雅可比矩阵中。由于这种做法，我们称每个误差项对应的优化变量为
参数块（Parameter Block）。
• 整体误差由很多小型误差项之和组成的问题，其增量方程的求解会具有一定的稀疏
性（会在第十讲详细讲解），使得它们在大规模时亦可求解。
• 其次，如果使用李代数表示，则该问题是无约束的最小二乘问题。但如果用旋转矩阵
（变换矩阵）描述位姿，则会引入旋转矩阵自身的约束（旋转矩阵必须是正交阵且行
列式为 1）。额外的约束会使优化变得更困难。这体现了李代数的优势。
• 最后，我们使用了平方形式（二范数）度量误差，它是直观的，相当于欧氏空间中距
离的平方。但它也存在着一些问题，并且不是唯一的度量方式。我们亦可使用其他的
范数构建优化问题。
简单的最小二乘问题

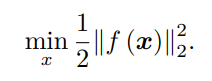
若f是一非线性函数，甚至有m维，对于这类问题一般采用迭代的方法。
1.给定某个初始值 x0。
2.对于第 k 次迭代，寻找一个增量 ∆xk，使得 ∥f (xk + ∆xk)∥22 达到极小值。
3.若 ∆xk 足够小，则停止。
4.否则，令 xk+1 = xk + ∆xk，返回 2
这让求解导函数为零的问题，变成了一个不断寻找梯度并下降的过程。直到某个时刻
增量非常小，无法再使函数下降。此时算法收敛，目标达到了一个极小，我们完成了寻找
极小值的过程。在这个过程中，我们只要找到迭代点的梯度方向即可，而无需寻找全局导
函数为零的情况，那么问题是如何求增量∆xk 。
求解增量最直观的方式是将目标函数在 x 附近进行泰勒展开：

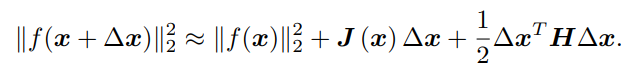
这里 J 是 ∥f(x)∥2 关于 x 的导数（雅可比矩阵），而 H 则是二阶导数（海塞（Hessian）
矩阵）。我们可以选择保留泰勒展开的一阶或二阶项，对应的求解方法则为一阶梯度或二
阶梯度法。如果保留一阶梯度，那么增量的方向为：

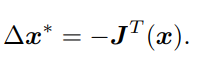
它的直观意义非常简单，只要我们沿着反向梯度方向前进即可。当然，我们还需要该方向上取一个步长 λ，求得最快的下降方式。这种方法被称为最速下降法。另一方面，如果保留二阶梯度信息，那么增量方程为：

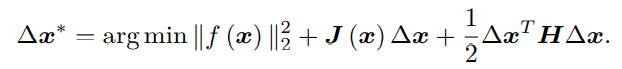
要使得最小，进行求导，∆x在等式中只含零次项、一次项、二次项，那么求导并令为0，则：

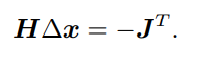
但存在H，增加计算量。
高数牛顿法它的思想是将 f(x) 进行一阶的泰勒展开（请注意不是目标函数 f(x)2）：

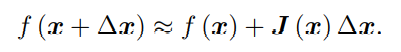
这里 J(x) 为 f(x) 关于 x 的导数，实际上是一个 m × n 的矩阵，也是一个雅可比矩阵。根据前面的框架，当前的目标是为了寻找下降矢量 ∆x，使得 ∥f (x + ∆x)∥2 达到最小。为了求 ∆x，我们需要解一个线性的最小二乘问题：

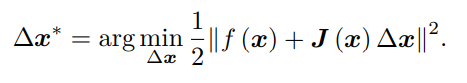
于是先开方，再对∆x进行求导，并令其为0，如下：

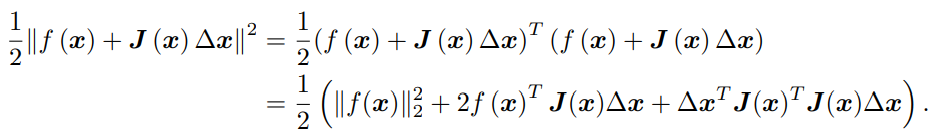
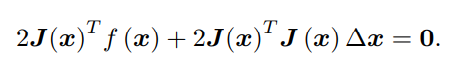
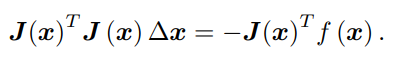
我们要求解的变量是 ∆x，因此这是一个线性方程组，我们称它为增量方程，也可以称为高斯牛顿方程 (Gauss Newton equations) 或者正规方程 (Normal equations)。我们把左边的系数定义为 H，右边定义为 g，那么上式变为：
注意注意注意这里的f(x)是误差是误差是误差！！！

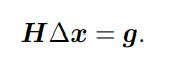
这里把左侧记作 H 是有意义的。对比牛顿法可见，高斯牛顿法用 JT J 作为牛顿法中二阶 Hessian 矩阵的近似，从而省略了计算 H 的过程。求解增量方程是整个优化问题的核心所在。如果我们能够顺利解出该方程，那么高斯牛顿法的算法步骤可以写成：
1.给定初始值 x0。
2.对于第 k 次迭代，求出当前的雅可比矩阵 J(xk) 和误差 f(xk)。
3.求解增量方程：H∆xk = g.
4.若 ∆xk 足够小，则停止。否则，令 xk+1 = xk + ∆xk，返回 2
对代码的理解，如下：
slambook2/ch6/gaussNewton.cpp

#include <iostream>
#include <chrono>
#include <opencv2/opencv.hpp>
#include <Eigen/Core>
#include <Eigen/Dense>
using namespace std;
using namespace Eigen;
int main(int argc, char **argv) {
    
    
  double ar = 1.0, br = 2.0, cr = 1.0;         // 真实参数值
  double ae = 2.0, be = -1.0, ce = 5.0;        // 估计参数值
  int N = 100;                                 // 数据点
  double w_sigma = 1.0;                        // 噪声Sigma值
  double inv_sigma = 1.0 / w_sigma;
  cv::RNG rng;                                 // OpenCV随机数产生器
  vector<double> x_data, y_data;      // 数据
  for (int i = 0; i < N; i++) {
    
    
    double x = i / 100.0;
    x_data.push_back(x);
    y_data.push_back(exp(ar * x * x + br * x + cr) + rng.gaussian(w_sigma * w_sigma));
  }
  int iterations = 100;    // 迭代次数
  double cost = 0, lastCost = 0;  // 本次迭代的cost和上一次迭代的cost
  chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
  for (int iter = 0; iter < iterations; iter++) {
    
    
    Matrix3d H = Matrix3d::Zero();             // Hessian = J^T W^{-1} J in Gauss-Newton
    Vector3d b = Vector3d::Zero();             // bias
    cost = 0;

    for (int i = 0; i < N; i++) {
    
    
      double xi = x_data[i], yi = y_data[i];  // 第i个数据点
      double error = yi - exp(ae * xi * xi + be * xi + ce);
      Vector3d J; // 雅可比矩阵
      J[0] = -xi * xi * exp(ae * xi * xi + be * xi + ce);  // de/da
      J[1] = -xi * exp(ae * xi * xi + be * xi + ce);  // de/db
      J[2] = -exp(ae * xi * xi + be * xi + ce);  // de/dc
      H += inv_sigma * inv_sigma * J * J.transpose();//关于inv_sigma,首先代码里赋值为1，并未改变数值
      b += -inv_sigma * inv_sigma * error * J;		 //其次再解方程会抵消掉，实际效果不清楚
      cost += error * error;
    }
    // 求解线性方程 Hx=b
    Vector3d dx = H.ldlt().solve(b); //ldlt()为进行LDLT分解
    if (isnan(dx[0])) {
    
    
      cout << "result is nan!" << endl;
      break;
    }
    if (iter > 0 && cost >= lastCost) {
    
    		//cost与上一次相同则结束
      cout << "cost: " << cost << ">= last cost: " << lastCost << ", break." << endl;
      break;
    }
    ae += dx[0];
    be += dx[1];
    ce += dx[2];
    lastCost = cost;
    cout << "total cost: " << cost << ", \t\tupdate: " << dx.transpose() <<"\t\testimated params: " << ae << "," << be << "," << ce << endl;
  }
  chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
  chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);
  cout << "solve time cost = " << time_used.count() << " seconds. " << endl;
  cout << "estimated abc = " << ae << ", " << be << ", " << ce << endl;
  return 0;
}

第三讲

第四讲

猜你喜欢