串匹配
串匹配问题即是:如何在字符串数据中,检测和提取以字符串形式给出的某一局部特征一般的,即:
对基于同一字符表的任何文本串T(|T|=n)和模式串P(|P|=m):
判定T中是否存在某一子串与P相同
若存在(匹配),则报告该子串在T中的起始位置
测评标准及策略
如何对任一串匹配算法的性能作出客观的测量和评估,多数人首先会想到采用算法性能的常规口径和策略:以时间复杂度为例,假设文本串T和模式串P都是随机生成的,然后综合其各种组合从数学或统计等角度得出结论。很遗憾,此类构思不适用。例如:
以基于字符表{0,1}的二进制串为例。任何长度为n的文本串,其中长度为m的串不过n-m+1个(m << n时接近n个)。另一方面,长度为m的随机模式串多达2^m个,故匹配成功的概率为n/2^m。以n=100000、m=100为例,这一概率仅有:
100000/2^100 < 10^-25
对于更长的模式串、更大的字符表,这一概率还将更低。因此,这一方法不能有效地覆盖成功匹配的情况,所得测评结论无法准确地反映算法的总体性能。
实际上,有效的涵盖成功匹配情况的策略时,随机选取文本串T,并且从T中随机取出长度为m的模式串
蛮力算法
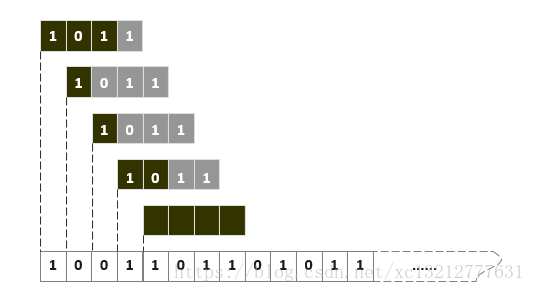
最直观的解法就是,自左向右以字符为单位,逐个移动模式串,直到在某个位置发现匹配,如下图所示:
具体有两种方法实现,两者原理相同,过程相仿,实现如下:
版本1:
int patternmatch(string T,string P)
{
int m=P.size();
int n=T.size();
int i,j;
for(i=0;i<n-m+1;++i)
{
for(j=0;j<m;++j)
if(T[i+j]!=P[j])
break;
if(j>=m) break;
}
return i;
}版本2:
int patternmatch(string T,string P)
{
int m=P.size();
int n=T.size();
int i=0,j=0;
while(i<n&&j<m)
{
if(T[i]==P[j])
{
++i;
++j;
}
else
{
i=i-j+1;
j=0;
}
}
return i-j;
}复杂度:在最好的情况下只需要经过一轮的比较即可,此时为O(m);在最坏的情况下,每一轮比对都要比较到模式串的末尾,且在最后一次比对成功,此时共要比较m*(n-m+1)次,则复杂度为O(n*m)。在m越大的时候,最坏的情况出现的概率越大
KMP算法
为了对蛮力算法进行改进,我们从最坏的情况分析入手。可以发现,在每一轮m次的比对中,仅最后一次可能失配。而一旦发生失配,文本串、模式串的字符指针都要回退,并且从头开始下一轮尝试。这样就会使得,之前匹配过的字符再次进行比较,实际上这类重复的字符比对操作没有必要,既然这些字符在前一轮的迭代中已经接受过比较,并且成功,我们也就掌握了它们的所有信息,我们可以利用这些信息来提高匹配算法的效率。例如:
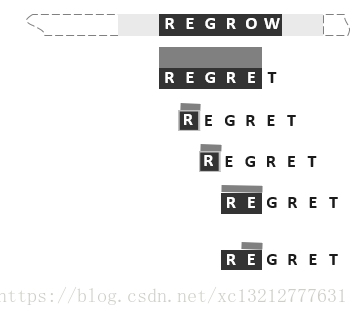
对于上图,在失配之后,可以直接跳过中间的三步,而直接到最后一步。这一技巧即:利用以往的成功比对所提供的信息(记忆),不仅可以避免文本串字符指针的回退,而且可以使模式串尽可能大跨度的右移(经验)。
- next表
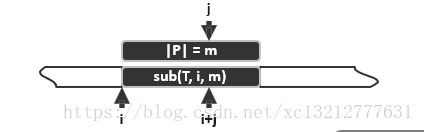
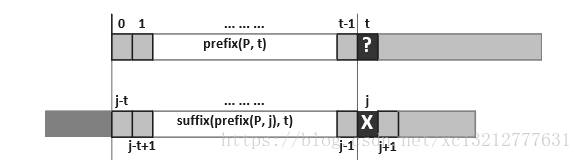
一般地,如下图所示当比对终止于T[i]!=P[j]。根据上面的想法,指针i不必回退,而是将T[i]与P[t]对齐并且开始下一轮的比较,那么t取多少?
上述满足的条件是:
P[0,t)=T[i-t,i)=P[j-t,j]
即,在P[0,j)中长度为t的真前缀,应该与长度为t的真后缀完全匹配,故t来自集合:
N(p,j)={ t | prefix(prefix(P, j), t) = suffix(prefix(P, j), t), 0 =< t < j}
一般而言,该集合中包含多个这样的t。其中具体的由哪些t值组成,仅取决于模式串P以及前一轮比对的首个失衡的位置P[j],而与文本串T无关。为了避免回溯,且知道位移量与t的大小成反比,所以:
next[j] = max(N(p,j))
则一旦发现P[j]与T[i]失配,即可转而将P[ next[j] ]与T[i]彼此对准开始下一轮的比对。
next表构造:
对于j>0则必有0在N(p,j)中,从而可以保证在其中取最大值,但是当j=0时该如何定义?在串匹配的过程中,如果在某一轮比对中首字符就失配,此时我们要将P直接右移一个字符,然后进行下一轮比对。所以在模式串前面加一个*作为通配符,让他与任何字符匹配,因此,我们可以取next[0]=-1。此时可以考虑如何求next表,考虑如下图:
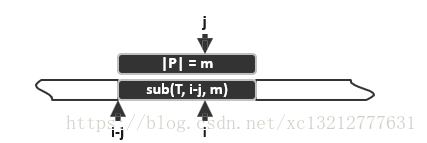
若next[j]=t,则意味着在P[0,j)中,自匹配的真前缀和真后缀的最大长度为t,所以必有next[j+1]<=next[j]+1,特别地当P[j]=P[t]时取等号,而当P[j]!=P[t]时该如何求next[j+1]?此时看如下图:
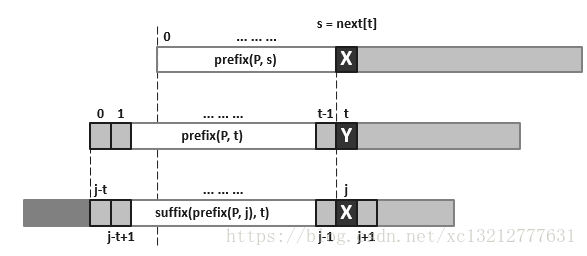
根据next表的功能定义,next[j+1]的下一个候选者依次是next[next[j]]+1,next[next[ next[j] ]+1……即挑选N(P,j)中的次大着继续比对。在此过程中,t必然单调递减,同时当t降到0时,必然会终止于通配的next[0]=-1,不至于下溢。
具体的可以实现如下:
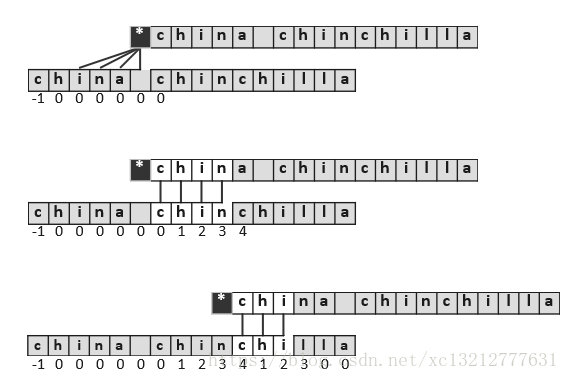
int *buildNext(char*p)
{
size_t m=strlen(p),j=0;
int *N=new int[m]; //next表
int t=N[0]=-1;
while(j<m-1)
{
if(t<0||p[j]==p[t]){
j++;t++;
N[j]=t;
}else
t=N[t];
}
return N;
}这一过程完全等效于模式串的自我匹配过程,下面看个实例如下:
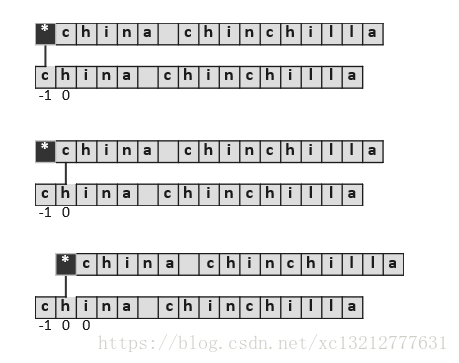
根据以上分析,可以得到KMP算法实现如下:
int match(char*P,char*T)
{//kmp算法
int *next=buildnext(P);//构建next表
int n=strlen(T),i=0;
int m=strlen(P),j=0;
while(j<m && i<n)
if(j<0||T[i]==P[j])//若匹配。判断次序不可以交换,j<0对应通配符的情况
{i++;j++;}
else
j=next[j];
delete [] next;
return i-j;
}复杂度分析:对于上面代码while循环至多执行2n次(这里不做证明),就KMP算法本身而言,运行时间不超过O(n),next表的构造与上述过程无本质区别,next表的构造时间为O(m),因此,KMP算法总的时间为O(m+n)。
改进KMP算法
尽管上述中的算法,已经达到了线性的时间,但是在某些情况下可以改进。
例如:
T = “000100001“
P = “00001“
next[ ] = {-1,0,1,2,3}
匹配过程如下:
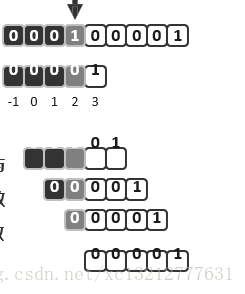
即:
T[3] 与 P[3] 比对,失败;与 P[next[3]] = P[2] 继续比对,失败;与 P[next[2]] = P[1] 继续比对,失败 ;与 P[next[1]] = P[0] 继续比对,失败;最终,才前进到 T[4]
其实已经知道P[0] = P[1] = P[2] = P[3] = ‘0’ (无需T串,即可在事先确定!),所以可以完全避免上述的三次比对。
就之前的KMP算法而言,我们使用next表实质就是利用以往成功比对的经验,将记忆力转换为预知力。同样我们可以利用失败的比对作为教训,同样可以从中受益。把这种“教训”引入next表,改进next表:
N(p,j) = {0 =< t < j | P[0, t)=P[j-t, j) 且 P[t]!=P[j]}
也就是说,除了自匹配长度以外,t还必须同时满足当前字符对不匹配的必要条件,才可以作为next表的候选,实现如下:
int *buildNext(char*p)
{
size_t m=strlen(p),j=0;
int *N=new int[m]; //next表
int t=N[0]=-1;
while(j<m-1)
{
if(t<0||p[j]==p[t]){
j++;t++;
N[j]=(p[j]!=p[t]? t : N[t]);
}else
t=N[t];
}
return N;
}改进后的算法原算法的唯一区别在于,每次在P[0, j )中发现长度为t的真前缀和真后缀相互匹配之后,还需要检查P[j]是否等于P[t]。只有在两个不等的时候,才可以将t赋给next[j];否则转而代之以next[t]。