串的kmp匹配算法

引言

串的模式匹配的基本概念是：给定主串S与模式串T，模式串t从s中位序为pos的字符开始往后匹配，在模式串中以第1位字符匹配主串的第pos位字符。如果相等，则开始比较pos位的后继位字符。否则，由主串的下一个字符开始起重新与模式串的字符进行匹配。当主串S中出现与模式串T完全相同的字符串序列时，则证明匹配成功。这种串匹配的过程主要用于字符串检查。

正文

KMP算法的核心优点在于：假设主串为 $s_{1}s_{2}s_{3}...s_{n}$ ，待匹配的模式串为‘ $p_{1}p_{2}p_{3}...p_{n}$ ’，当主串在第i位，模式串在第j位失去匹配（即 $s_{i}\neq p_{j}$ 时），可以将模式串向后滑动尽可能多的距离进行匹配。这种方式可以尽可能多地减少主串与模式串指针的回溯，从而降低算法的复杂度。由核心优点产生的主要问题是，既然处于失配的条件下，主串的第i个字符应当与模式串中的哪一个字符进行匹配（相当于求模式串允许向后滑行的距离）。

假设以下几个量，设：主串中失配的坐标为i，模式串中失配的坐标为j，后一次过程将主串s中的第i个字符与模式串的第k个字符进行比较（k<j），模式串中前k-1个字符的子串存在如下规律

‘ $p_{1}p_{2}p_{3}...p_{k-1}=s_{i-k+1}s_{i-k+2}...s_{i-1}$

与此同时，由于串的结构是字符逐个对应的，s串的i位置的前k个字符一一对应p串j位置的前k个字符。则已经得到的匹配结果为：

$p_{j-k+1}p_{j-k+2}..p_{j-1}=s_{i-k+1}s_{i-k+2}...s_{i-1}$

由以上两个式子有以下结论：

$p_{1}p_{2}p_{3}...p_{k-1}=p_{j-k+1}p_{j-k+2}...p_{j-1}$

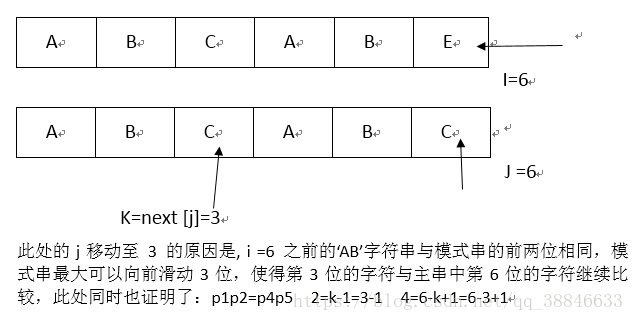
模式串中有着以上的结论：前k-1个位置的字符与失配位置前k-1个字符具有一一对应的关系。在移动完成后，需要重新检验模式串位置为k的字符与主串位置为i的字符是否相等。具体如下图所示：

kmp算法的必要过程是建立一个名为next的数组，建立完成后，需要在匹配之前求出假若位序为j（相当于第j+1个字符）的字符失配时，在模式串中需要移动的距离k。即每一个next[j]=k式子之中k的值。

匹配的整体过程如下：1）假设i的初始值为pos，j的初始值为1 2）进行条件判断，若 $s_{i}=p_{j}$ ，则i与j分别增加1。 3）若在此处模式串失配了，则i不变，同时j移动至next[j]的位置，继续返回过程2进行条件判断 4）过程3终止的条件有两种，一是出现字符串匹配，则i，j同时加1，继续匹配过程 二是当j通过next[j]进行递推后，当j最终为-1时，i 与 j需要同时加1（主串s的第i个字符与模式串p中第1个字符不相同，需要重新匹配s中第 i +1位字符）

在了解了kmp算法的整体过程后，需要掌握的是算法最大的难点：如何求出k的值。主要的方法是利用递归以及假设法

（1）当 j = 0 时，next [0] = -1，j初始化为-1，按以上的思路，之后 i 与 j 均需要加1 ，即模式串p的首位p[0]与主串s的i+1位字符s[i+1]开始匹配

（2）当 j = 1 时，next[1]=0，此时的 j 指针只能后移到下标为0，位序为1的字符。

（3）j 取任意自由值时，假设next [j]= k，此时由模式串p的性质易得以下结论： $p_{1}p_{2}p_{3}...p_{k-1}=p_{j-k+1}p_{j-k+2}...p_{j-1}$ ，此时，不可能存在k' >k会满足以上的结论。在以上的结论下有两种假设：

假设一： $p_{k}=p_{j}$

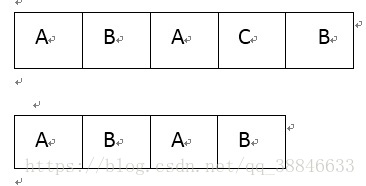
此时模式串中满足以下结论 $p_{1}p_{2}...p_{k-1}p_{k}=p_{j-k+1}p_{j-k+2}...p_{j-1}p_{j}$ ，next [ j+1]=k+1=next [ j ] +1 ，具体的示意图如下：

假设二： $p_{k}\neq p_{j}$

在该种情形下， $p_{1}p_{2}...p_{k}\neq p_{j-k+1}p_{j-k+2}..p_{j}$ ，这种情形下求next函数值可以等价于一个模式匹配：用模式串p去匹配主串p，由此时的已知条件 $p_{1}p_{2}...p_{k-1}=p_{j-k+1}p_{j-k+2}..p_{j-1}$ 可以求得，下标由1开始至k的字符与由j-k+1开始至下标 j-1的字符对应相等。换言之，相当于是需要将模式串滑动至下标为next[k]的字符，再将其与 $p_{j}$ 进行比较。假设next[k]=k'，且 $p_{j}=p_{k'}$ ，可以借助假设一的结论，推出: next[ j+1]=k'+1=next[k]+1 。若 $p_{k'}\neq p_{j}$ ，继续进行以上k=next[k]循环，直到 $p_{k'}=p_{j}$ 为止。若始终不存在某个k'满足字符匹配，则将next[j+1]赋值为0.

KMP算法的修正：

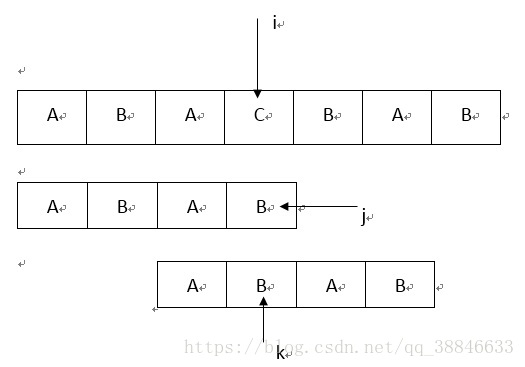
按以下图片中给出的案例：

其中next[0]= -1，next[1]=0，next[2]=0，next[3]=1，而不难发现，当位序为4的字符失配时，需要转至位序为2的字符，使得 $s_{4}$ 与 $p_{2}$ 继续进行匹配，但模式串中的 $p_{2}$ 字符与 $p_{4}$ 字符均是字符B，所以仍然是失配的状态，需要继续访问 $p_{next[1]}$ 字符。修正算法的条件是：若出现next[j]=k,同时又有 $p_{j}=p_{k}$ 时，主串 $s_{i}$ 需要直接与 $p_{next[k]}$ 进行比较。

KMP算法的求next数组操作：

void getnext(Hstring h,int next[max])
{
    next[0]=-1;
    int j=0;
    int k=-1;
    while(j<h.length-1)
    {
        if(k==-1||h.ch[j]==h.ch[k])
            {
                ++j;
                ++k;
                if(h.ch[j]!=h.ch[k])
                {
                    next[j]=k;
                }
                else
                {
                    next[j]=next[k];
                }
            }
    }
}

KMP算法的整体操作函数：

int KMP(Hstring h1,Hstring h2,int pos,int next[max])
{
    int i=pos;
    int j=0;
    while(i<=h1.length&&j<=h2.length)
    {
        if(j==-1||h1.ch[i]==h2.ch[j])
        {
            ++i;
            ++j;
        }
        else
        {
            j=next[j];
        }
    }
    if(j==h2.length)
    {
        return i-j;
    }
    else
    {
        return -1;
    }
}

猜你喜欢