一、整数划分问题
整数划分问题是算法中的一个经典命题之一,有关这个问题的讲述在讲解到递归时基本都将涉及。所谓整数划分,是指把一个正整数n写成如下形式:
n=m1+m2+...+mi; (其中mi为正整数,并且1 <= mi <= n),则{m1,m2,...,mi}为n的一个划分。
如果{m1,m2,...,mi}中的最大值不超过m,即max(m1,m2,...,mi)<=m,则称它属于n的一个m划分。这里我们记n的m划分的个数为f(n,m);
例如但n=4时,他有5个划分,{4},{3,1},{2,2},{2,1,1},{1,1,1,1};
注意4=1+3 和 4=3+1被认为是同一个划分。
该问题是求出n的所有划分个数,即f(n, n)。下面我们考虑求f(n,m)的方法;
1.递归法:
根据n和m的关系,考虑以下几种情况:
(1)当n=1时,不论m的值为多少(m>0),只有一种划分即{1};
(2)当m=1时,不论n的值为多少,只有一种划分即n个1,{1,1,1,...,1};
(3)当n=m时,根据划分中是否包含n,可以分为两种情况:
(a)划分中包含n的情况,只有一个即{n};
(b)划分中不包含n的情况,这时划分中最大的数字也一定比n小,即n的所有(n-1)划分。
因此 f(n,n) =1 + f(n,n-1);//这里就根据f的定义,由于划分中不包含n,最大的数字一定比n小,即比m小,所以f中第二个数为最接近n的数——n-1,而前一个数就是n,因为是对n进行划分,具体与下面f(n-m,m)处道理一样(个人理解,求不吐槽)
(4)当n<m时,由于划分中不可能出现负数,因此就相当于f(n,n);
(5)但n>m时,根据划分中是否包含最大值m,可以分为两种情况:
(a)划分中包含m的情况,即{m, {x1,x2,...xi}}, 其中{x1,x2,... xi} 的和为n-m,因此这情况下
为f(n-m,m)//这里开始一直看不懂,后来才明白一些:注意这里的前提是划分包含m,所以将m提出来一个,保证划分中一定会有m,剩下数字划分的和为n-m,而这n-m中可能不会出现m,也可能出现m,但由于我们已经提出了一个m,所以此处不用担心m是否再出现。根据f的定义,后f中的第二个数就是m了,而第一个数为什么是(n-m),原因是提出一个m后,已经保证了划分中一定出现m,而n-m还没有进行划分,这里忽略提出的m,对剩下的整数n-m进行划分,划分的最大值仍然是m
(b)划分中不包含m的情况,则划分中所有值都比m小,即n的(m-1)划分,个数为f(n,m-1);
因此 f(n, m) = f(n-m, m)+f(n,m-1);
综上所述:
f(n, m)= 1; (n=1 or m=1)
f(n,m) = f(n, n); (n<m)
1+ f(n, m-1); (n=m)
f(n-m,m)+f(n,m-1); (n>m)
#include<iostream>
using namespace std;
int equationCount(int n,int m)
{
if(n==1||m==1)
return 1;
else if(n<m)
return equationCount(n,n);
else if(n==m)
return 1+equationCount(n,n-1);
else
return equationCount(n,m-1)+equationCount(n-m,m);
}
int main(void)
{
int n;
while(scanf("%d",&n)!=EOF&&(n>=1&&n<=120))
{
printf("%d\n",equationCount(n,n));
}
return 0;
}二、Hanoi问题
我们在使用程序实现它之前我们来分析分析汉诺塔的解法:
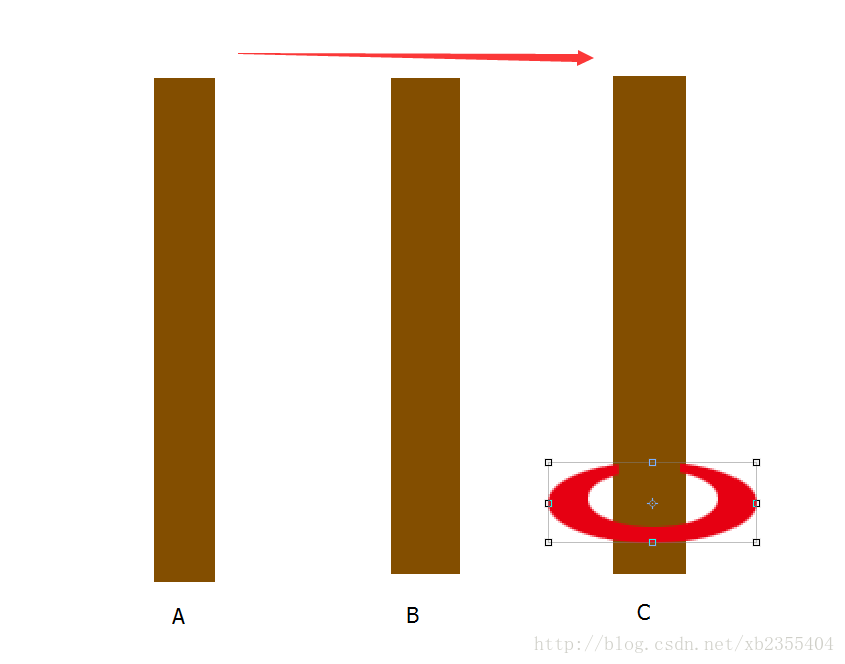
我们设定三个柱子A,B,C。我们的目的是将环从A–>C。
当N=1即一阶时它的路径很简单只需要从A->C进行移动。
当N=2时我们需要进行三步: 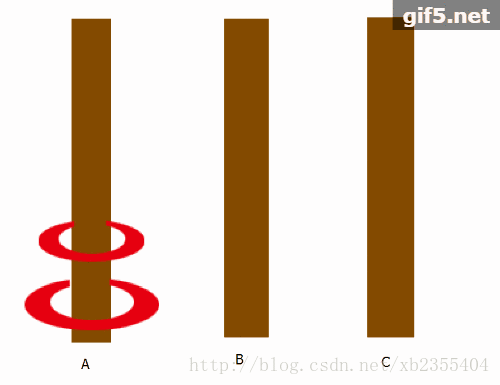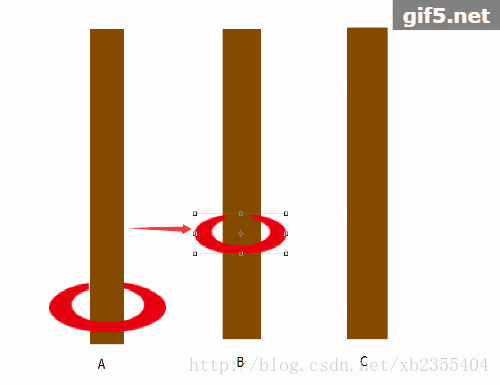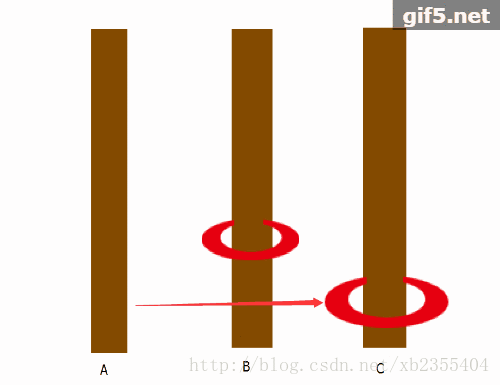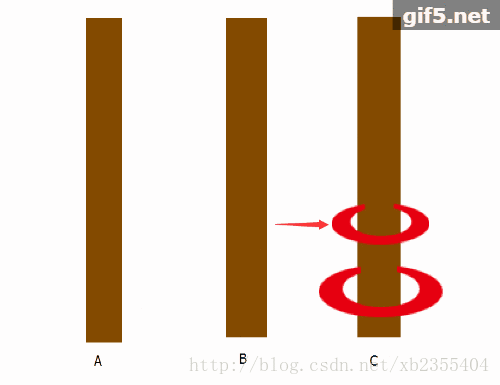
这里我制作了一个动图来演示了过程。当然N=3时中共7步8帧,由于繁琐的制图我就不继续使用动图演示了!
3阶汉诺塔其实我们都可以轻松的解决。
那么到底他们有什么共性呢?或者说和递归有什么联系呢?
我们还是来使用图片解释:
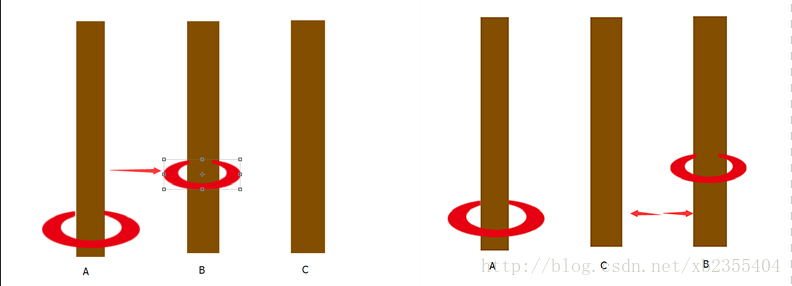
左图为2阶汉诺塔中间的步骤之一,我们已经将小环移动到了B柱,最大环此时可以视为不存在。那么如右图所示我们将B,C柱子交换位置,那么此步骤是否和移动1阶汉诺塔一样了呢?
然后我们中间执行了将最大环从A移动到C的固定步骤
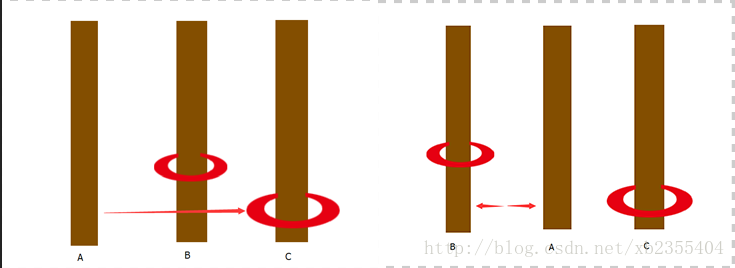
同理,在左图为2阶汉诺塔中间的步骤之一,我们已经将最大的环移动到了C柱,最大环此时可以视为不存在。那么如右图所示我们将A,B柱子交换位置,那么接下来的步骤是否和移动1阶汉诺塔一样了呢?
到这里我们总结出了如下特点:
其实2阶汉诺塔相当于执行了三大步骤:
1.在ACB的顺序下执行了一阶汉诺塔的移法
2.从A->C移动了最大盘
3.在BAC的顺序下执行了一阶汉诺塔的移法
那么推广到三阶的时候,我们将小环和中环视为一个整体,我们是否又变成了执行二阶汉诺塔方法了呢?
那么四阶前三个环视为整体,五阶前四个环视为整体……我们已经找到了解决汉诺塔方法的递归算法。下面,我们就用代码来实现它。
public class Hanoilmpl {
public void hanoi(int n, char A, char B, char C) {
if (n == 1) {
move(A, C);
} else {
hanoi(n - 1, A, C, B);//步骤1 按ACB数序执行N-1的汉诺塔移动
move(A, C); //步骤2 执行最大盘子移动
hanoi(n - 1, B, A, C);//步骤3 按BAC数序执行N-1的汉诺塔移动
}
}
private void move(char A, char C) {//执行最大盘子的从A-C的移动
System.out.println("move:" + A + "--->" + C);
}
public static void main(String[] args) {
Hanoilmpl hanoi = new Hanoilmpl();
System.out.println("移动汉诺塔的步骤:");
hanoi.hanoi(3, 'a', 'b', 'c');
}
}