递归、分治-整数划分问题

版权声明：转载请注明出处。 https://blog.csdn.net/baidu_38304645/article/details/83687135

将正整数n表示成一系列正整数之和。

n=n1+n2+...+nk;

其中n1>=n2>...>=nk>=1, k>=1

正整数n这种表示称为正整数n的划分。问题是求正整数n的不同划分个数。

例如正整数6有如下11种不同的划分

6；

5+1；

4+2，4+1+1；

3+3，3+2+1，3+1+1+1；

2+2+2，2+2+1+1，2+1+1+1+1；

1+1+1+1+1+1

输入：正整数n。

输出：n的不同划分个数。

运行结果：

分析：前面的几个例子中，问题本身都具有比较明显的递归关系，易用递归函数直接求解。

本例若设p(n)为正整数n的划分数，则难以找到递归关系

现考虑增加一个自变量，将最大加数n1不大于m的划分个数记做q(n,m).q(n,m)有如下递归关系。

(1) q(n,1) = 1 n>=1

当最大加数n1 不大于1时，任何正整数n只有一种划分形式，即

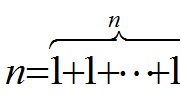
(2)q(n,m) = q(n,n), m>=n

最大加数n1 实际上不能大于n。因此，q(1,m) = 1.

(3)q(n,n) = 1 + q(n,n-1); n=m

正整数n的划分由n1=n的划分和n1<=n-1的划分组成。

(4)q(n,m) = q(n,m-1) + q(n-m,m), n > m > 1;

正整数n的最大加数n1,不大于m的划分，由n1 <= m-1的划分和n1=m的划分组成。

注意，正整数n的n1=m的所有划分形式为

m+m1+…+mi =n    where mj ≤ m, j=1,2,…,i

That is, m1+…+mi =n-m

因此，n的n1=m的划分个数是q(n-m, m)

所以，q(n,m)的递归关系：

q(n,m) =

1                                n=1, m=1

q(n,n)                         n<m

1 + q(n,n-1)                n=m

q(n,m-1) + q(n-m,m)   n>m>1

正整数n的划分数p(n) = q(n,n)

int q(int n, int m)
{
    if(n<1 || m<1)        //小于1说明不存在
        return 0;
    if(n==1 || m==1)      //只有一种划分形式
        return 1;
    if(m > n)             //最大加数m实际上不能大于n 因此q(1,m) = 1
        return q(n, n);
    if(n == m)            //正整数的划分由n1=n的划分和n1<=n-1的划分组成
        return q(n, m-1) + 1;
    return q(n, m-1) + q(n-m, m);    //由n1=m的划分和n1<=m-1的划分组成
}