从傅里叶到小波 3

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/poisonchry/article/details/80914127

从《从傅里叶到小波 1》给出了傅里叶公式的三角函数和形式，并且通过欧拉公式作为桥，将实数平面的三角函数和映射到了复平面上，于是在《从傅里叶到小波 2》中，有了我们常见的以复指数形式表达的傅里叶公式形式，并且给出了正交性的结论与表达方法。
在本章中，我们将试图证明傅里叶函数的收敛与收敛条件。如果傅里叶级数无法收敛，那么对于给定周期函数f(t)，我们就无法从数学定义上证明傅里叶级数可以拟合f(t)。

关于傅里叶级数的收敛性

这里我们将给出关于傅里叶级数收敛的证明，正如在之前的文章中所说，如果级数无法收敛，那么级数就没有应用的意义，我们之所以能使用这个数学工具去分析周期信号，就是因为傅里叶级数收敛这个关键因素。

通常，用纯数学的方法证明级数收敛，会使用L2平面和正余弦函数的正交性作为切入点，并且给出很多页的证明，论证收敛的充分必要条件，我们这里不打算采用这样的方法去证明，因为这篇《从傅里叶到小波》我们只打算做一些类似科普，或者说比科普稍微深入一点的说明，所以我们打算使用一种不完全的证明方法，以证明对于连续可积信号，它会满足这样一些性质或者说特征，使得傅里叶级数收敛。

首先，我们给出正弦函数的标准形式：$f(x) = A \cdot sin(nx + \phi) + C$，其中，A表示函数的振幅，n是角频率，$\phi$是相位，C是Y轴平移量。我们知道，无论修改$\phi$还是C，只会修改正弦函数在笛卡尔坐标里，XY轴上的位置，而对A的修改只是修改了正弦函数的振荡区间但不改变其频率，对频率真正有影响的，只有对n的修改，并且满足n值越大，频率越高的特点。

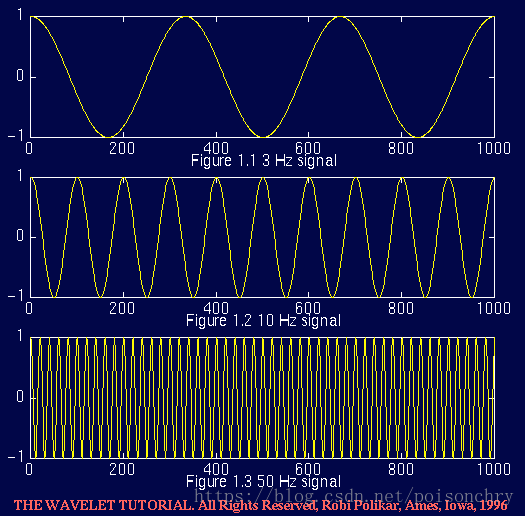
所以，我们如果用程序绘制不同频率的正弦函数，会得到这样一个图形：

因此如果对函数在正区间内进行积分，在一个$[0, \pi]$周期内，其积面积，必然与振幅A正相关，而与角频率负相关，所以我们可以得到：

$$\int_{0}^{\pi} sin(nx + \phi)dx \propto \frac{1}{n}$$

因此，当$n \to +\infty$，在正弦函数一个周期$[0, \pi]$内的积分就趋近于0，由于负轴方向也是一样的方法，所以，随着角频率的增大，正弦函数的积分趋近于0.

参考资料：

[1] “The wavelet tutorial”, Robi Polikar, January 12, 2001.

傅里叶分析与非周期信号

从热力学的角度看，这个世界不存在无限振荡的周期信号，即便是一个正弦信号，也会因为能量衰减，到最后某一时刻信号消失。所以说，正余弦信号，是理想的信号，因为它在正负轴无限延长，并且不存在能量衰减。

所以，严格来说，我们无法对非周期信号，或者有能量衰减的信号使用傅里叶分析。但是通过一些特殊的处理方法，我们可以让这些信号适用于傅里叶分析。

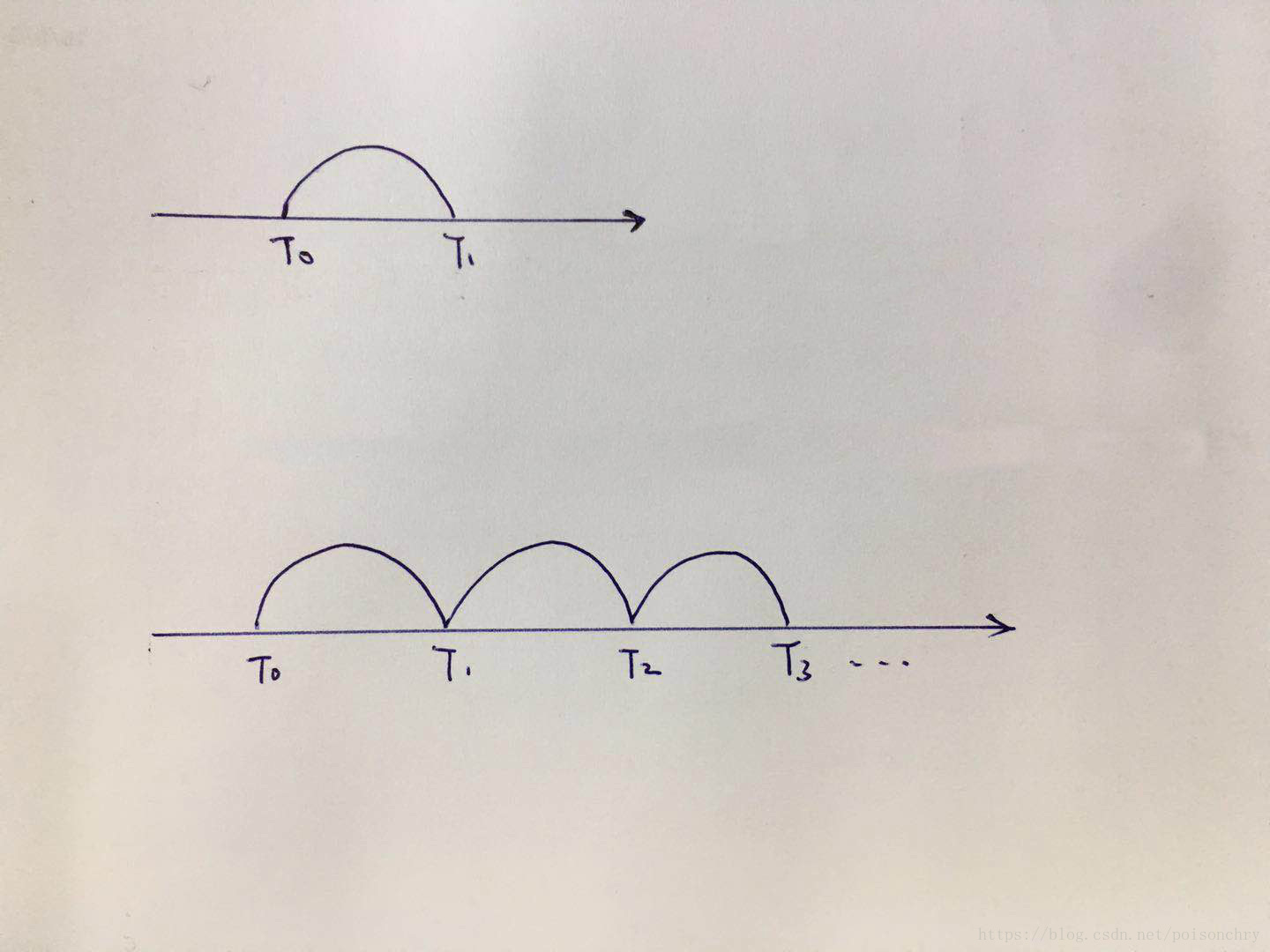
如果有一个非周期信号，$T_o$可以通过复制信号，使之成为周期信号，于是可以通过傅里叶分析获得信号包含的频率信息。这就是我们分析非周期信号常用的技巧。

如何阅读傅里叶频谱图

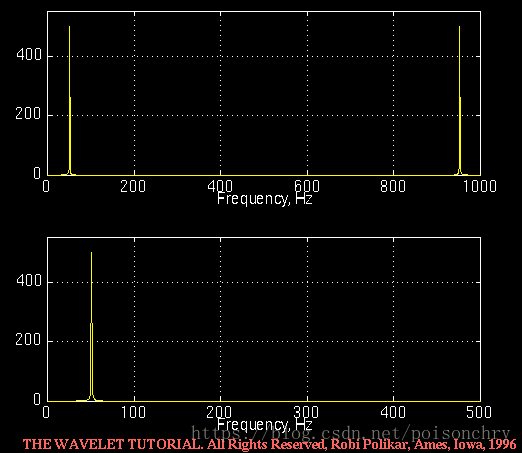
傅里叶分析由于对于信号进行了完整的时域分析，于是可以得出信号包含的全部频率信息。例如对于50Hz的正弦信号，通过FFT(Fast Fourier Transform)可以获得一个频谱图如下：

由于FFT算法采用蝶形计算，所以对比DFT(Discret Fourier Transform)，它的图形是对称的（这也是因为傅里叶级数是关于实轴对称的共轭复数，所以为了快速计算，算法设计者只处理了一半的数据），实际上我们只需要关心其图形的一半。坐标轴X上的数值表示对应第50个维度的地方，就是50Hz频率所在位置，因此，X轴也被称为正弦信号的频率。

而纵轴Y轴，数的含义则没有意义，参考傅里叶公式，我们可以知道由复数形式表示的傅里叶级数，其系数是一个包含了振幅、相位等信息的常熟，某些地方Y轴也被成为正弦信号的加权常数。

所以对于频率图来说，我们只关心在具体频率分量位置，是否常数>0。>0时，表示该频率存在，否则就是没有频率。在傅里叶频谱图上，当某个位置出现一个峰值时（peak），就说明在那个位置是有信号的。

那么，使用FFT之后，x轴上每个样本的频率是怎么计算的呢？

$$Freq(n) = n \times \frac{F_{sampling}}{Len(FFT)}$$

$F_{sampling}$是指信号采样率，时间为分钟，即你的程序是1分钟采样多少次数据，$Len(FFT)$是复数数组长度，比如你用1024长的复数数组计算某个信号的频率，n是对应的bin的频率。例如，采样率为1024Hz，FFT数组长度也是1024，那么对于：

bin 1 $\to$ 0 Hz
bin 2 $\to$ 1 Hz
……

这些知识点对于二维是一样的，所以很容易扩展到二维甚至高维情况。