从傅里叶到小波 4

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/poisonchry/article/details/81004560

关于傅里叶分析的缺点

使用傅里叶分析，可以对信号进行频率分析，但是由于傅里叶分析是对全时域的分析，所以它对于某些特殊信号频率在某时段的出现，以及突变信号，变频信号的分析就有不足。

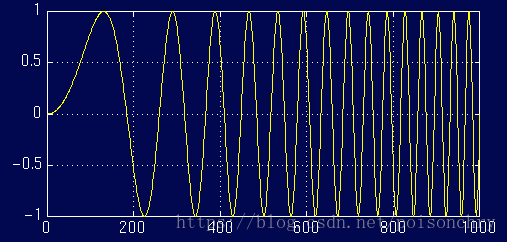
例如，对于如下变频信号1：

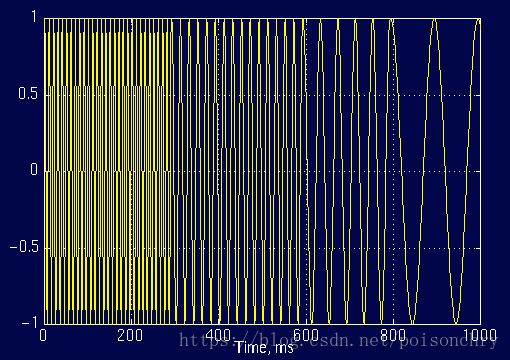
与变频信号2：

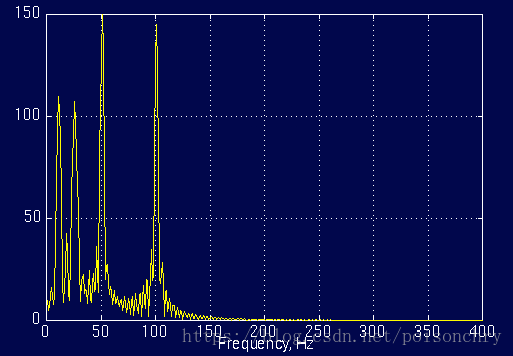
使用傅里叶分析，就会得到一样的频率图

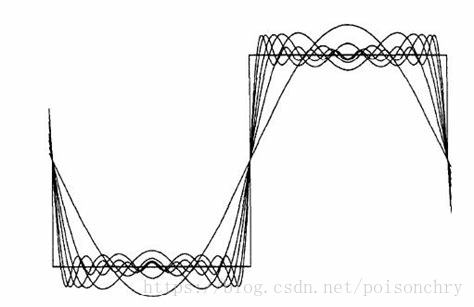
尽管频率分布都一样，但是我们无法从频率图上获得各频率出现的时间，或许你已经注意到了，与固定频率的周期信号相比，这个频率图上多出了很多锯齿状的频率分布，导致这个原因，也是傅里叶分析的另一个缺陷，它对于突变信号，非连续信号，需要使用大量高频信号去近似拟合，这也意味着傅里叶分析，对于这类信号，从而导致耗费大量的计算时间（吉布斯效应）。

傅里叶分析的改进方法——短时傅里叶方法（Short Time Fourier Transform）

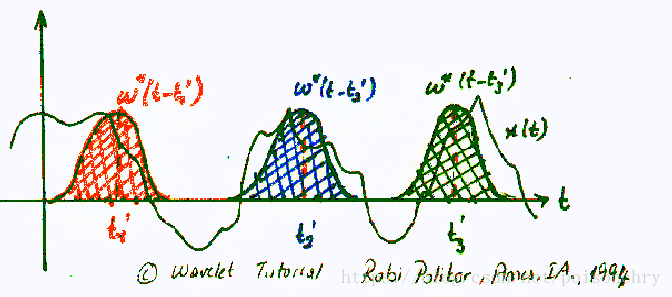
了解了傅里叶分析的基本概念，那么就很容易理解什么叫短时傅里叶方法，简写为STFT。它的核心思想是，将全局信号，依照时间间隔T，拆分为独立的信号块，再使用傅里叶分别求解各时间区间内的信号频率。

用公式进行表示，就是这样：

$$STFT(t, f) = \int_0^1 [f(t) \cdot \omega(t-t^*)] \cdot e^{-2\pi ikt} dt$$

其中，$f(t)$是原函数，$\omega(t)$ 是窗口函数，其中，$(t - t^*)$表示该函数在时间轴上的位移。如果我们将高斯函数作为平移窗口函数，那么对于信号$f(t)$，在$t_1, t_2, t_3$时段，对应窗口函数的数学表达就表示为$\omega(t - t_1), \omega(t - t_2), \omega(t - t_3)$。

这个过程，是个类似卷积的过程，如果我们用类似python的伪码表示这个过程，需要处理的数据有三个，一个是信号原始，一个是窗口函数，最后一个是对于一维信号$f(t)$，窗口函数$\omega(t)$在时间轴上的位移量，T，那么STFT函数的表示为：

function window_shifting(window_fun, start_time, signal_size): 
    wind = [signal_size]
    set elements in win to zero
    for i = start_time to signal_size:
        wind[i] = window_fun[i]
    return win

function mat_dot(signal, window):
    if len(signal) is not len(window):
        return false
    for i = 0 to len(signal):
        signal[i] = signal[i] * window[i]
    return signal


function STFT(signal, window, T)
    shifted_window = window_shifting(window, T, len(signal))
    result = mat_dot(signal, shifted_window)

    if result is not false:
        res = fft(result)
        return res

从上示例看，其实window是一个随时间移动的滤波器，常用的滤波器有理想滤波器，也有高斯滤波器，个人需要针对自己的具体需要选择合适的滤波器。

参考资料：
[1] “The wavelet tutorial”, Robi Polikar, January 12, 2001.