从傅里叶到小波 2

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/poisonchry/article/details/80896471

关于连续傅里叶公式的推导

在上一篇《从傅里叶到小波 1》中已经给出了欧拉公式的推导和三角函数和的表达式，虽然三角函数和就是傅里叶公式的表达形式，但是数学家们还是嫌这样的表达式过于累赘，于是试图偷懒，通过将实数平面的三角函数和投影到复平面，简化计算公式。

三角函数和：

$$f(t) = A_0 + \sum_{k=1}^{n} A_k \cdot (a_k cos2 \pi kt+b_k sin2 \pi kt)$$

欧拉公式：

$$e^{ix} = cosx + i sinx$$

在某些教科书中，$A_0$ 用 $\frac{a_0}{2}$ 代表，并且它们给出了一个不令人信服的推导，这里 $\frac{a_0}{2}$ 的含义，主要应用在电子、电气专业上，被称为“直流分量”，因为实际生活中的电信号是正弦波（由交流电发电机导致），所以电子电气专业里，电信号的表示为：直流分量 + 正弦信号叠加。

由此，我们通过欧拉公式，将三角函数的和，映射到复平面，于是得到如下表达式：

$$f(t) = \sum_{k=-n}^{n} C_k e^{2\pi i k t}$$

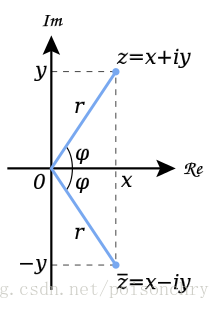
因为在复平面，复数存在共轭关系，$C(x, y) = x + i y, \overline{C(x, y)} = x - iy$，$\left | C(x, y) \right | = \left | \overline{C(x, y)} \right |$，为了完整表示实数平面内三角级数的加和，在复平面的范围变成了$[-n, n]$。

至此，我们获得了以指数$e$为基的傅立叶级数的表达式，对比三角级数的表达式，我们可以发现$C_k$中包含了振幅信息，相位信息，还有频率信息。但是如果假设我们已经获得了$f(t)$ 函数，如何求解$C_k$呢？

首先从等式的基本定义出发，$f(t) = C_{-n}e^{2 \pi i (-n) t} + C_{-n+1}e^{2 \pi i (-n +1) t} + \cdots$

所以我们可以得到这样的数学形式：

$$C_m e^{2 \pi i m t} = f(t) - \sum_{k \neq m} C_k e^{2\pi i k t}$$

两边求$e^{-2 \pi i m t}$，于是可以得到：

$$C_m = f(t) \cdot e^{-2 \pi i m t} - \sum_{k \neq m} C_k e^{2\pi i (k-m)t}$$

为了求解公式，我们对公式两侧的数学表达式进行求积分：

$$\int C_m dt = \int f(t) \cdot e^{-2 \pi i m t} dt - \int \sum_{k \neq m} C_k e^{2\pi i (k-m)t} dt$$

由于计算的周期已经从$[-\pi, \pi]$ 通过 $2 \pi t$ 变为了 $[0, 1]$，所以

$$\int_0^1 C_m dt = \int_0^1 f(t) \cdot e^{-2 \pi i m t} dt - \int_0^1 \sum_{k \neq m} C_k e^{2\pi i (k-m)t} dt$$

对上式分别求积分，于是：

$$\int_0^1 C_m dt = C_m$$

展开 $\int_0^1 \sum_{k \neq m} C_k e^{2\pi i (k-m)t} dt$，对每一项$\int_0^1 C_k e^{2\pi i (k-m)t} dt$ 单独求积分，于是

$$\int_0^1 C_k e^{2\pi i (k-m)t} dt = \frac{C_k}{2 \pi i (k-m)}e^{2\pi i (k-m)t} |_0^1$$

$$= \frac{C_k}{2 \pi i (k-m)} (e^{2\pi i (k-m)} - e^0)$$

$$\because k \neq m$$

$$\frac{C_k}{2 \pi i (k-m)} (e^{2\pi i (k-m)} - e^0) = \frac{C_k}{2 \pi i (k-m)} 0$$

于是，我们可以得到这样一个表达式

$$C_k = \int_0^1 f(t) \cdot e^{-2 \pi i k t} dt$$

结合上面推导的表达式，我们得到傅里叶级数的正、逆表达式 $C_k = \int_0^1 f(t) \cdot e^{-2 \pi i k t} dt$ 和 $f(t) = \sum_{k=-n}^{n} C_k e^{2\pi i k t}$

关于正交性

由三角函数的推导，我们可以得到如下的结果：

$$\int_{-\pi}^{\pi} 1 \cdot 1dt = 2 \pi$$
$$\int_{-\pi}^{\pi} cos(nt) \cdot sin(mt)dt = \left\{\begin{matrix} 0, m \neq n\\ \pi, m = n \end{matrix}\right.$$
$$\int_{-\pi}^{\pi} cos(nt) \cdot cos(mt)dt = \left\{\begin{matrix} 0, m \neq n\\ \pi, m = n \end{matrix}\right.$$
$$\int_{-\pi}^{\pi} sin(nt) \cdot sin(mt)dt = \left\{\begin{matrix} 0, m \neq n\\ \pi, m = n \end{matrix}\right.$$

正交性是非常重要的一个特征，通过正交性我们可以求解出三角级数的参数。