从傅里叶到小波 1

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/poisonchry/article/details/80840211

关于无穷级数

对于计算机来说，绝大多数数据是可以当作信号来处理的，而信号处理的焦点，多集中在对信号的时域（temporal domain）、频域（frequency domain）的分析。试想一下，一首优美动听的音乐，如果用五线谱进行表示，是有不同的音符和节拍组成的。对于信号来说，五线谱就是这段音乐的时频信息，包含在什么时候演奏什么音高，一小节时常多少，每个音符的演奏时常是多少，而这是频率信息。

通过时间和频率信息，那么可以告知我们的乐手，如何去演奏一首音乐。但是，反过来，要将一段优美的音乐转换为五线谱，是需要花费一些时间和精力，并且依赖于谱写者对于音准（频率分析）和时间的准确把握。

现在我们回到一个基本的问题，我们可以很容易从等式左边，得出右边的值，但是从等式右边，则很难回溯它是由哪些数组成的，例如：

$$1+2+3=6$$

与

$$6=？+？+？$$

我们用（0，1，5），（0，2，4），（1，1，4）等组合解这个问题。这样的问题或许还比较容易处理，但给定一个复杂的函数，我们怎样用最简函数进行表达呢，比如，对于$e^x$，$sinx$，我们该怎样表达呢？

所以，为了解决这个问题，数学家们提出了无穷级数的概念，说到底也就是微分法，通过构造大量极限为0的子函数，去无限逼近函数方程$F(x)$的结果。

那么，回到我们刚才的问题，如果这个这个数列是这样的：

$$f(x) = 1 + 2 + 3 + 4 + 5 + 6 + 7 + \cdots + n + (n+1) + \cdots$$

它是不是一个级数呢？答案是肯定的，但是对于我们求解问题没有任何意义。首先，我们给出无穷级数的定义如下：

若有一个无穷数列:

$$u_1,u_2,u_3,\cdots ,u_n,\cdots$$ 此数列构成下列表达式: $$u_1+u_2+u_3+\cdots +u_n+ \cdots$$ 称以上表达式为常数项无穷级数（infinite series），简称级数，记为: $$\sum_{n=1}^{\infty }u_n=u_1+u_2+u_3+\cdots +u_n+ \cdots$$

因此，对于一个无穷的数列，它构成一个级数，而这个级数的$\sum$，有发散和收敛两种结果。

例如，如果是$1+2+3+\cdots+n$那么这个最终加和是$s_n=\frac{(a_1+a_n)\times n}{2}$，$n>0$的时候，那么这个$S_n$就是一个趋于无限大，我们称这个数列是个发散数列。反过来，如果一个数列类似这样$16, 8, 4, 2, 1, 0.5, 0.25, \cdots$按照通项公式，如，$\frac{1}{2^{n}}$这样，那么这个数列加和时，它的$\sum$就会收敛，因此这个数列就是个收敛数列。

在这里，我们信号处理，无论是傅里叶分析还是小波分析，其实都可以认为是收敛的无穷级数的扩展应用。在正式开始介绍傅里叶分析前，首先我们来回顾一下无穷级数的某些性质：

• 无穷级数收敛的一个必要条件是它的通项以0为极限；
• 若有一个无穷级数且它是收敛的，那么每一项乘以一个常数，则其和等于$a\sum$；
• 若有多个无穷级数，并且都是收敛的，那么它们可以逐项相加或相减，其极限值是多个收敛的无穷级数的极限值之和或差；
• 若有一个无穷级数且它是收敛的，那么对它增加或减去有限项，不影响其收敛性，但新的极限值不一定相等；
• 若有一个无穷级数且它是收敛的，那么对它的各项加括弧组成的新级数，也是收敛的，且极限值等于原来的极限值，反之，不一定收敛。

参考资料：

[1] 《无穷级数的定义与基本性质》

关于正弦波叠加

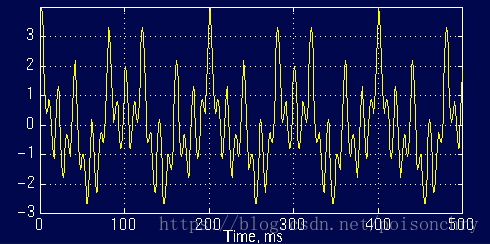
有这样一个关于时间t的周期信号，它由如下的公式$\sum$得到：

$$f(t) = cos(2 \pi \cdot 10\cdot t) + cos(2 \pi \cdot 25\cdot t) + cos(2 \pi \cdot 50\cdot t) + cos(2 \pi \cdot 100\cdot t)$$

需要注意一点的是，cos函数与sin函数，仅仅只有一个$\frac{\pi}{2}$的相位差。

在实际中，我们只能得到一个关于时间t复杂的周期信号，而无法得到一个包含频率信息的周期信号。所以问题回到我们前面，我们能否通过有限简单的正弦函数（三角函数）去近似模拟一个周期信号呢？

答案是，如果这个信号是周期信号，那么是可以通过有限加和三角函数去模拟复杂的周期信号的，也就是回到无穷级数的定义和应用上。我们把上式做个归纳，并将全部信号以正弦信号加和进行表示。从无穷级数的定义出发，我们可以得到这样一个三角函数的加和公式：

$$f(t) = A_0 + \sum_{k=1}^n A_k \cdot sin(2\pi kt + \phi)$$

现在我们已经获得了傅立叶级数的三角函数形式的表达式。但是用这样的一个级数进行表达，对于数学家来说，过于累赘了（因为包含三个变量，振幅$A_k$，相位$\phi$，角频率k），接下来我们要使用三角函数的变形，对这个表达式进行适当的调整。

在正式变换函数表达式前，我们先引入三角函数的和差化积变换式
$cos(\theta + \phi) = cos \theta cos \phi - sin \theta sin \phi$
$sin(\theta + \phi) = sin \theta cos \phi + cos \theta sin \phi$

根据三角函数和差化积变形式，我们可以对上式进行变换

$$sin(2\pi kt + \phi) = sin 2 \pi kt \cdot cos \phi + cos 2 \pi kt \cdot sin\phi$$

我们令$cos \phi = b_k$，$sin\phi = a_k$，则上式为：

$$sin(2\pi kt + \phi) = a_k cos 2 \pi kt + b_k sin 2 \pi kt$$

所以，原式变为：

$$f(t) = A_0 + \sum_{k=1}^n A_k \cdot (a_k cos 2 \pi kt + b_k sin 2 \pi kt)$$

之所以要变形为这个样子，是为了我们之后将欧拉公式代入后，把函数从实数平面映射到复平面做准备。

欧拉公式

目前，我们所有加和，都是在实数平面内的，因此需要我们使用至少三个变量去描述这个正弦加和，有没有简单点的表示方法呢？数学家们发现，如果用复数e表示，我们可以大大简化表达式中的变量。所以，我们将函数从实数平面，映射到复平面，也称阿尔冈平面。

而实数平面与复数平面的映射关系，由欧拉公式作为“桥”，将三角函数与复数联系在了一起，这里我们来推导一下欧拉公式。

首先，我们用泰勒级数分别展开$e^x$，$sinx$，$cosx$

$$e^x=1 + \frac{x}{1!} + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots + \frac{x^n}{n!}$$
$$cos(x) = 1 - \frac{x^2}{2!} +\frac{x^4}{4!}-\frac{x^6}{6!}+\cdots$$
$$sin(x)=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots$$

在$e^x$中，将x替换为$jy$，那么表达式就变为：

$$e^{jy} = 1 + \frac{jy}{1!} + \frac{(jy)^2}{2!} + \frac{(jy)^3}{3!} + \cdots$$ 其中， $j$代表虚数， $j^2 = -1$，所以：

$$e^{jy} = 1 + \frac{jy}{1!} - \frac{y^2}{2!} + \frac{(jy)^3}{3!} + \frac{y^4}{4!} + \cdots$$

所以：

$$e^{jy}=(1- \frac{y^2}{2!} + \frac{y^4}{4!} + \cdots) + (jy - \frac{jy^3}{3!} + \frac{jy^5}{5!} + \cdots)$$

于是我们推导出欧拉公式：

$$e^{jy} = cos(x) + j \cdot sin(x)$$

参考资料：

[1] 《欧拉公式》
[2]《泰勒级数》

P.S. 从傅立叶到小波分析，是非常庞杂而系统的知识，鉴于工作量巨大，我写到这里的时候决定分成几部分，所以……现在推导到这里，只完成了一小部分……