从傅里叶到小波 6

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/poisonchry/article/details/81069595

在上一篇文章《从傅里叶到小波5》解释了小波变换是从短时傅里叶概念的衍生，从它们的函数形式也可以看出二者之间的相似。现在，我们观察小波变换的数学表达式， $CWT_{x}^{\psi}(\tau, s) = \Psi_{x}^{\psi}(\tau, s) = \frac{1}{\sqrt{|s|}} \int f(t) \cdot \psi^*(\frac{t - \tau}{s}) dt$ ，小波基函数 $\Psi = \psi^*(\frac{t - \tau}{s})$ 与滤波器的有些类似。我们知道，对频域使用滤波器，可以过滤高频信号和低频信号，而对时域信号进行滤波，通常是作平滑处理，但反过来说，被平滑掉的“锯齿”，实际上也是原始信号的高频部分，从这个意义讲小波变换，起到了一个信号分流器的角色，将原始信号过滤为高频和低频部分，那么它又是如何具体工作的呢？

为解释这个问题，我们需要回到时域信号的基本特点。

时域信号的基本特点

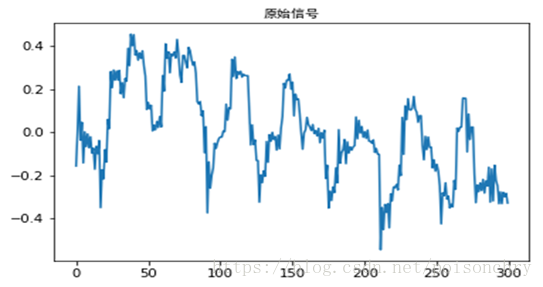
这是一个采样率为30Hz，采集时间为350s的原始时域信号，因为高频信号快速振荡的特点，可以在较短的观察周期里清晰的看见，而低频信号由于振荡较慢，所以需要一个较长的观察周期才能够发现。

• 低频信号 ——> 振荡较慢 ——> 需要较长的观测周期 ——> 频域上能有更好的体现
• 高频信号 ——> 振荡较快 ——> 需要较短的观测周期 ——> 时域上能有更好的体现

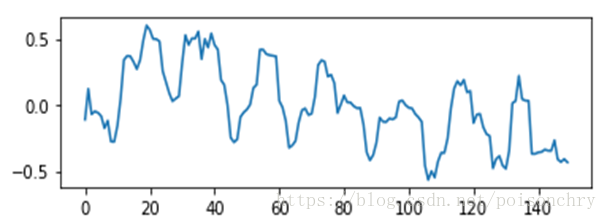
所以，如果我们使用某种平滑函数，也就是时域滤波器对原信号卷积，那么就可以把原始信号上的“毛刺”给剔除掉，例如用线性平滑函数，对该信号进行处理，那么可以得到一个平滑后的图：

小波函数

为了理解小波变换的原理，你首先需要把小波函数 $\psi^*$ 当成一个时域滤波器，只不过这个滤波器和我们常见的滤波器，例如二阶的高斯滤波器，一阶的带通滤波器，或者其他样条滤波器不太一样，小波函数之所以叫小波（Wavelet），顾名思义，它有在有限位置振荡，积分为0，可以拉伸和压缩等较其他常用的滤波器所不一样的特殊属性。

$$CWT_{x}^{\psi}(\tau, s) = \Psi_{x}^{\psi}(\tau, s) = \frac{1}{\sqrt{|s|}} \int f(t) \cdot \psi^*(\frac{t - \tau}{s}) dt$$

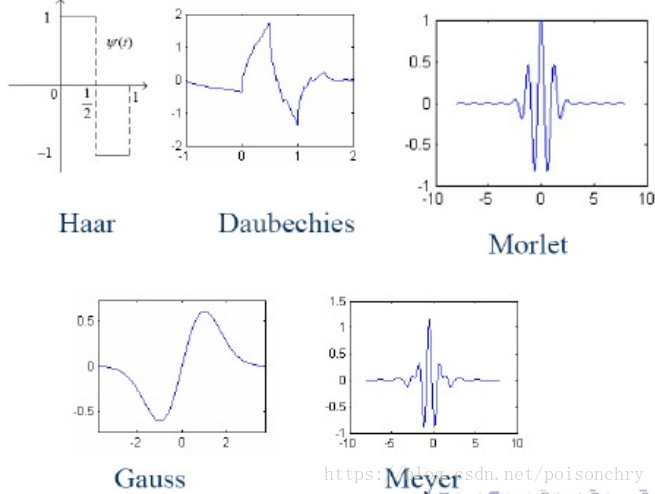
这些是比较常用的小波函数，它们都是在有限空间里振荡能量衰减，并且积分为0的函数。由于小波本身具备滤波器的性质，所以要知道过滤后的信号的形态特征上，多多少少会带上小波函数的形态特征。

对原始信号的小波分解

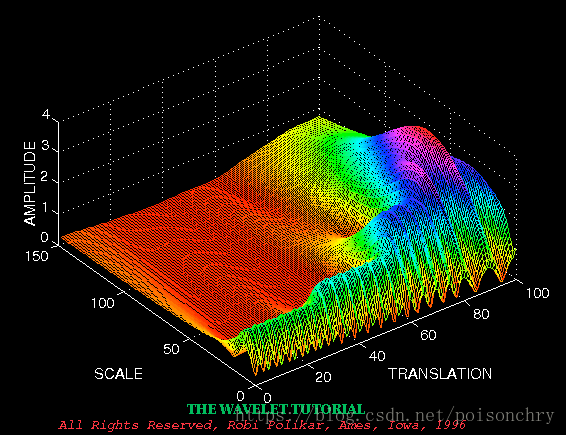
由于小波函数的振荡特点，所以当我们对X轴进行压缩，可以得到以高频信号，反之可以得到一个低频信号，由于小波函数只在有限区间内振荡，所以需要在每次计算完毕后，对小波函数进行平移，从$T_0$，移动到$T_1$ 然后对原信号做卷积，再移动到下一个时刻$T_2$，一直覆盖完毕全部原始信号，我们可以得到一个关于时间、尺度、频率分布的图，如果以三维形式 plot 出来，大概就是这样的：

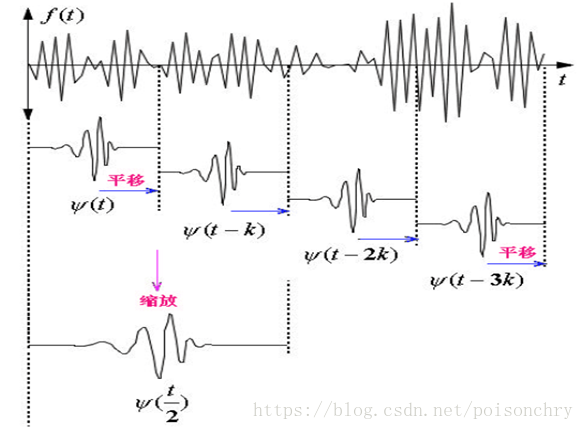
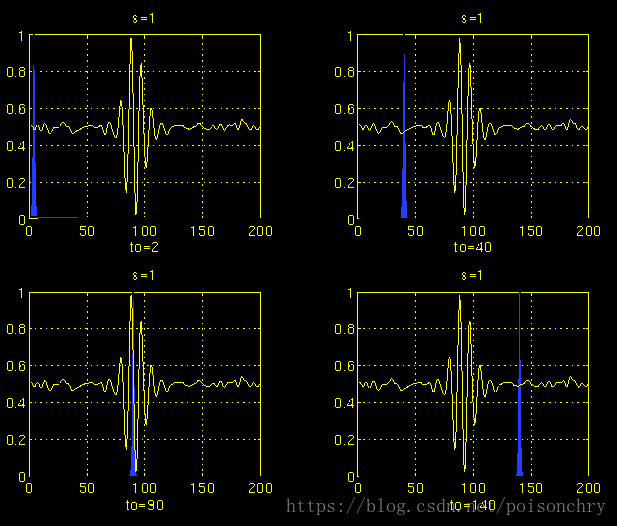
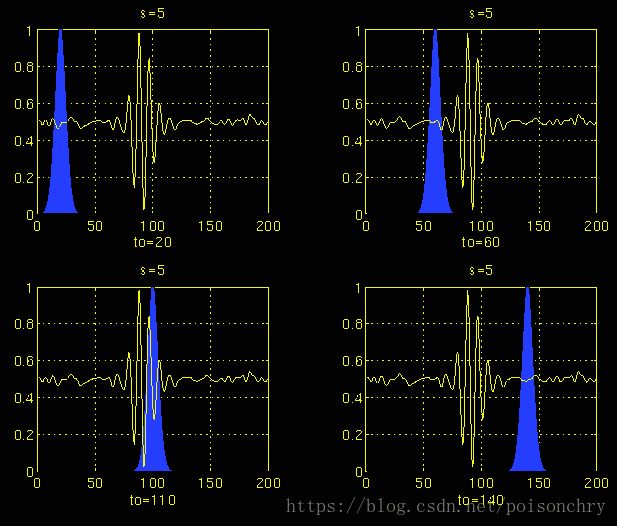
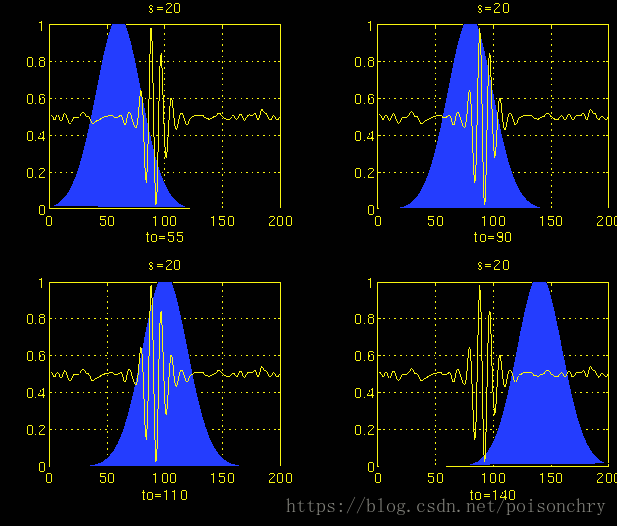
用示例图表示计算过程，我们可以看到小波变换总是从最小尺度（也就是最高频率）开始计算，需要注意一点就是尺度和频率的换算方式$freq = 1 / scale$

第一次计算

第二次计算

第三次计算

……

其中蓝色部分，就是小波函数，黄色的信号代表原始信号。

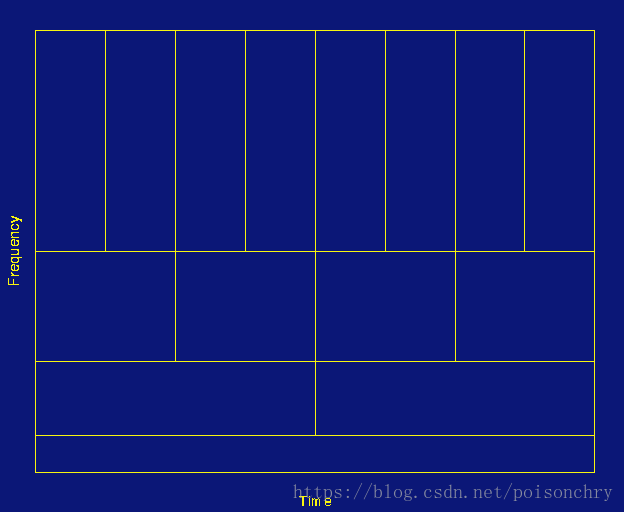
对于连续小波变换，它的控制参数由两个参数$s, \tau$控制，分别表示小波函数的缩放scale大小的s，和时间轴平移距离$\tau$。为了保证“对齐”，小波函数总是遵循$2^n$的形式进行缩放和平移的。在某些文章或教程里，你可以看到这样一个格子用来说明小波的特点，但在中文教材里缺很少会详细解释这个格子的意思

格子的横坐标代表时间坐标t，纵坐标代表的是频率，格子的数量从最下层到最上层，数量以$2^n$增加，这告诉我们，随着频率增高，需要的计算次数也在增加；

每个格子的面积，也就是小波函数振荡部分对原信号函数的积分区域是一样的，这使得小波在不同尺度上，可以尽最大可能覆盖对应的频率范围，换句话说，就是用大尺度小波函数对信号中低频信号进行积分，可以最大尺度捕捉到低频信号部分，反之则是高频信号。

所以，由于各格子的宽度，也就是观测窗口，是随着频率一起调整，所以这也是小波分析相较于短时傅里叶，说它是一种动态分析的原因。