（一）泊松分布是什么

泊松分布是用于近似二项分布的情况的。二项分布有两个参数，一个是事件发生的概率p，一个是试验的总数n。当p非常小且n也有一定大的时候（n大于等于20，p小于等于0.05），就可以用泊松分布来近似二项分布，用泊松分布来近似二项分布的好处是计算方便。

（二）泊松分布公式以及通俗地推导过程

泊松分布公式：

$P(X=k)=\frac{\lambda ^{k}e^{-\lambda }}{k!}$

通俗推导：

假设某一零件厂每天生成的次品数如下：

周一	周二	周三	周四	周五
3	7	4	6	5

均值为：

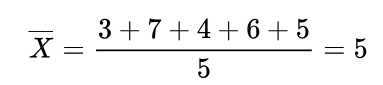
假设我们把每天工厂生产时间设为T：

再把T分为n=4份，并把周一生产出的三个次品放进去：

扫描二维码关注公众号，回复： 4121092 查看本文章

此时工厂在每个时间段生成次品的概率就如同抛硬币，要么出现，要么不出现，这样子工厂生产次品的概率符合二项分布：

$\binom{4}{3}p^{^{3}}(1-p)^{^{1}}$

但当把数据换成周二的7个次品呢？

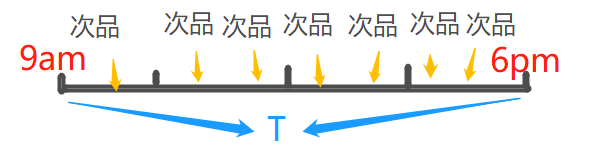
则出现每个时间段多余一个次品的情况，这样的话就不符合二项分布了。要使其符合二项分布，就必须使n变大，现在让我们把n=8：

这样子又能符合二项分布了：

$\binom{8}{7}p^{7}(1-p)^{^{1}}$

即只要不出现一个时间段内出现两个次品的情况，就能用二项分布解决。

为了达成一个时间段内不出现两个次品的条件，我们干脆把n趋向于无穷，因为n越大，T分成的时间段就越多：

更抽象一点，T时间里出现k个次品的概率为：(式子1)

上式中，n趋于无穷，k是可以确定的，那么p应该怎么求呢？

上面的式子1，已经符合二项分布的，而二项分布的期望为：

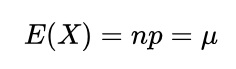
因此：

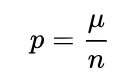----（式子2）

有了式子2后，式子1可以变成：

计算这个极限：

因为当 $n \to \infty$ 时：

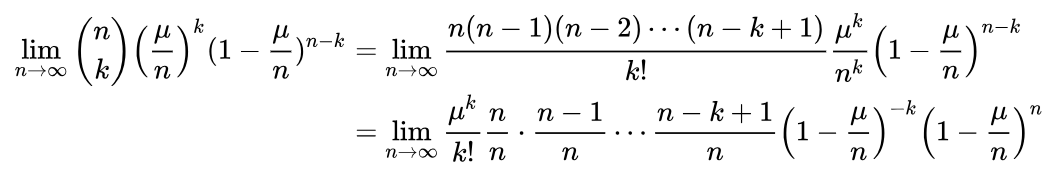
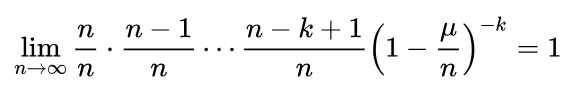
所以：

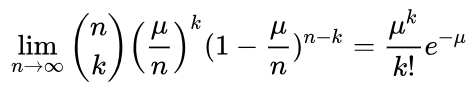
最后把 $\mu =\lambda$ ，得到泊松分布的概率密度函数的公式：

画出概率密度函数：

当k=8时，绿色部分加起来为0.93，即每天生产次品不超过8个的概率为0.93

（三）总结：

当p十分小且n也比较大的时候可以推荐用泊松分布（n大于等于20，p小于等于0.05）。

（四）例题分析计算

计算机硬件公司制造某芯片，次品率为0.1%，各芯片称为次品相互独立，求在1000个产品中至少有2只次品的概率，以X记产品中的次品数。

解：

用二项分布：

$P\left \{ X\geq 2 \right \}=1-P\left \{ X=0 \right \}-P\left \{ X=1 \right \} =1-(0.999)^{^{1000}}-\binom{1000}{1}(0.999)^{999}(0.001)\approx 0.2642411$

用泊松分布计算：

由提： $\lambda =1000\times 0.001=1$ ，代入泊松分布的式子：

$P\left \{ X\geq 2 \right \}=1-P\left \{ X=0 \right \}-P\left \{ X=1 \right \}=1-e^{-1}-e^{^{-1}}\approx 0.2642411$

显然用泊松分布计算方便一点。

概率论---泊松分布