机器学习——EM算法及代码实现

EM算法作用

EM算法是一种迭代算法，用于含有隐变量的概率模型参数的极大似然估计或极大后验估计。
预备知识：
用Y表示观测随机变量的数据，Z表示隐随机变量的数据。Y和Z连在一起称为完全数据，观测数据Y又称为不完全数据。给定观测数据Y，其概率分布是P(Y|θ)，其中θ是需要估计的模型参数，它相应的对数似然估计L(θ)=logP(Y|θ)。假设Y和Z的联合概率分布是P(Y,Z|θ),那么完全数据的对数似然函数是logP(Y,Z|θ)。
EM算法通过迭代求L(θ)=logP(Y|θ)的极大似然估计。每次迭代包含两步：E步，求期望；M步，求极大化

EM算法：

输入：观测变量数据Y，隐变量数据Z，联合分布P(Y,Z|θ)（也即完全数据的概率），条件分布P(Z|Y,θ)（也即未观测数据Z的条件概率分布）；
输出：模型参数θ；
（1）选择参数的 $θ^0$ ,开始迭代；
（2）E步：记 $θ^i$为第i次迭代参数θ的估计值，在第i+1次迭代的E步，计算

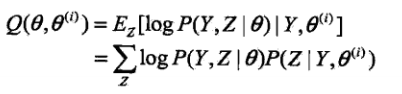
这里P(Z|Y, $θ^i$)是在给定观测数据Y和当前的参数估计 $θ^i$下隐变量数据Z的条件概率分布；
（3）M步：求使Q(θ， $θ^i$)极大化的θ，确定第i+1次迭代的参数估计值 $θ^（i+1)$;

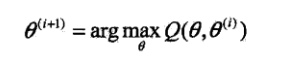
（4）重复第(2)步和第(3)步，直到收敛。
下面对上面所提Q函数做如下解释：
Q函数：完全数据的对数似然函数P(Y,Z|θ)关于在给定观测数据Y和当前参数 $θ^i$下对未观测数据Z的条件概率分布P(Z|Y, $θ^i$)的期望称为Q函数

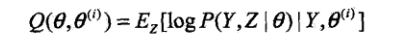
EM算法几点重要说明：
（1）参数的初值可以任意选择，但需注意EM算法对初值是敏感的。
（2）E步求Q(θ， $θ^i$)。Q函数式中Z是未观测数据，Y是观测数据。注意的是，Q(θ， $θ^i$)的第1个变元表示要极大化的参数，第2个变元表示参数的当前估计值。每次迭代实际在求Q函数及其极大。
（3）M步求Q(θ， $θ^i$)的极大化，得到 $θ^（i+1)$，完成一次迭代 $θ^i$-> $θ^（i+1)$。
（4）停止迭代的条件，一般是对较小的正数A，若满足|| $θ^（i+1)$- $θ^i$||<A，则停止迭代。
EM算法求最佳参数θ代码如下：

# -*- coding: utf-8 -*-

import numpy as np
import math  
import copy  
import matplotlib.pyplot as plt  

isdebug = True

# 指定k个高斯分布参数，这里指定k=2。注意2个高斯分布具有相同均方差Sigma，均值分别为Mu1,Mu2。  
def init_data(Sigma,Mu1,Mu2,k,N):  
    global X  
    global Mu  
    global Expectations  
    X = np.zeros((1,N))  
    Mu = np.random.random(k)  
    Expectations = np.zeros((N,k))  
    for i in range(0,N):
        if np.random.random(1) > 0.5:  
            X[0,i] = np.random.normal(Mu1, Sigma)
        else:  
            X[0,i] = np.random.normal(Mu2, Sigma)
    if isdebug:  
        print("***********")
        print("初始观测数据X：")
        print(X )
        
# EM算法：步骤1，计算E[zij]  
def e_step(Sigma, k, N):  
    global Expectations  
    global Mu  
    global X  
    for i in range(0,N):
        Denom = 0 
        Numer = [0.0] * k
        for j in range(0,k):
            Numer[j] = math.exp((-1/(2*(float(Sigma**2))))*(float(X[0,i]-Mu[j]))**2)  
            Denom += Numer[j]
        for j in range(0,k):
            Expectations[i,j] = Numer[j] / Denom  
    if isdebug:  
        print("***********")
        print("隐藏变量E（Z）：")
        print(Expectations)
        
# EM算法：步骤2，求最大化E[zij]的参数Mu  
def m_step(k,N):  
    global Expectations  
    global X  
    for j in range(0,k):
        Numer = 0  
        Denom = 0  
        for i in range(0,N):
            Numer += Expectations[i,j]*X[0,i]  
            Denom +=Expectations[i,j]  
        Mu[j] = Numer / Denom
        
# 算法迭代iter_num次，或达到精度Epsilon停止迭代  
def run(Sigma,Mu1,Mu2,k,N,iter_num,Epsilon):  
    init_data(Sigma,Mu1,Mu2,k,N)  
    print("初始<u1,u2>:", Mu)
    for i in range(iter_num):  
        Old_Mu = copy.deepcopy(Mu)  
        e_step(Sigma,k,N)  
        m_step(k,N)  
        print(i,Mu)
        if sum(abs(Mu - Old_Mu)) < Epsilon:  
            break  

if __name__ == '__main__':
    sigma = 6   # 高斯分布具有相同的方差
    mu1 = 40    # 第一个高斯分布的均值 用于产生样本
    mu2 = 20    # 第二个高斯分布的均值 用于产生样本
    k = 2       # 高斯分布的个数
    N = 1000    # 样本个数
    iter_num = 1000 # 最大迭代次数
    epsilon = 0.0001    # 当两次误差小于这个时退出
    run(sigma,mu1,mu2,k,N,iter_num,epsilon)  
   
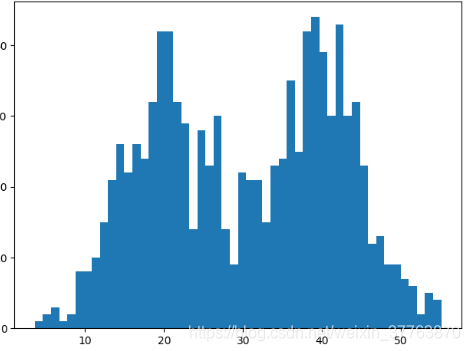
    plt.hist(X[0,:],50)
    plt.show()