快速傅里叶变换和快速卷积算法
1. 快速傅里叶变换
有限长序列的傅里叶变换公式为
X ( k ) = D F T [ x ( n ) ] = ∑ n = 0 N − 1 x ( n ) W N k n , W N = e − j 2 π N … … ( 1 ) X(k)=DFT[x(n)]=\sum\limits_{n=0}^{N-1}x(n)W_{N}^{kn},W_N=e^{-j\frac{2\pi}{N}}\,……(1) X(k)=DFT[x(n)]=n=0∑N−1x(n)WNkn,WN=e−jN2π……(1)
将序列x(n)按奇偶分为两个系列
{ x 1 ( r ) = x ( 2 r ) x 2 ( r ) = x ( 2 r + 1 ) , r = 0 , 1 , . . . , N 2 − 1 \begin{cases}x_1(r)=x(2r)\\x_2(r)=x(2r+1)\end{cases},r=0,1,...,\frac{N}{2}-1 {
x1(r)=x(2r)x2(r)=x(2r+1),r=0,1,...,2N−1
于是
X ( k ) = ∑ r = 0 N / 2 − 1 x ( 2 r ) W N k 2 r + ∑ r = 0 N / 2 − 1 x ( 2 r + 1 ) W N k ( 2 r + 1 ) X(k)=\sum\limits_{r=0}^{N/2-1}x(2r)W_N^{k2r}+\sum\limits_{r=0}^{N/2-1}x(2r+1)W_N^{k(2r+1)} X(k)=r=0∑N/2−1x(2r)WNk2r+r=0∑N/2−1x(2r+1)WNk(2r+1) = ∑ r = 0 N / 2 − 1 x 1 ( r ) W N / 2 k r + W N k ∑ r = 0 N / 2 − 1 x 2 ( r ) W N / 2 k r k = 0 , 1 , . . . , N − 1 … … ( 2 ) =\sum\limits_{r=0}^{N/2-1}x_1(r)W_{N/2}^{kr}+W_N^k\sum\limits_{r=0}^{N/2-1}x_2(r)W_{N/2}^{kr}\,k=0,1,...,N-1\,……(2) =r=0∑N/2−1x1(r)WN/2kr+WNkr=0∑N/2−1x2(r)WN/2krk=0,1,...,N−1……(2)
设x1(n)和x2(n)的N/2点DFT分别为X1(k)和X2(k),带入(2)式中有
X ( k ) = X 1 ( k ) + W N k X 2 ( k ) , k = 0 , 1 , . . . , N 2 − 1 … … ( 3 ) X(k)=X_1(k)+W_N^kX_2(k),k=0,1,...,\frac{N}{2}-1\,……(3) X(k)=X1(k)+WNkX2(k),k=0,1,...,2N−1……(3)
为得到另一半k值的表达式,将(2)式中的k用k+N/2代替,即
X ( k + N 2 ) = ∑ r = 0 N / 2 − 1 x 1 ( r ) W N / 2 ( k + N / 2 ) r + W N k + N / 2 ∑ r = 0 N / 2 − 1 x 2 ( r ) W N / 2 ( k + N / 2 ) r X(k+\frac{N}{2})=\sum\limits_{r=0}^{N/2-1}x_1(r)W_{N/2}^{(k+N/2)r}+W_N^{k+N/2}\sum\limits_{r=0}^{N/2-1}x_2(r)W_{N/2}^{(k+N/2)r} X(k+2N)=r=0∑N/2−1x1(r)WN/2(k+N/2)r+WNk+N/2r=0∑N/2−1x2(r)WN/2(k+N/2)r = ∑ r = 0 N / 2 − 1 x 1 ( r ) W N / 2 k r − W N k ∑ r = 0 N / 2 − 1 x 2 ( r ) W N / 2 k r =\sum\limits_{r=0}^{N/2-1}x_1(r)W_{N/2}^{kr}-W_N^k\sum\limits_{r=0}^{N/2-1}x_2(r)W_{N/2}^{kr} =r=0∑N/2−1x1(r)WN/2kr−WNkr=0∑N/2−1x2(r)WN/2kr
即
X ( k ) = X 1 ( k ) − W N k X 2 ( k ) , k = N 2 , N 2 + 1 , . . . , N − 1 … … ( 4 ) X(k)=X_1(k)-W_N^kX_2(k),k=\frac{N}{2},\frac{N}{2}+1,...,N-1\,……(4) X(k)=X1(k)−WNkX2(k),k=2N,2N+1,...,N−1……(4)
由(3)(4)两式可知,一个N点DFT可以分解为两个N/2点DFT计算,这两个N/2点DFT计算通过(3)(4)两式的运算组合成N点DFT。这种运算的信号流图如下,因为形似蝴蝶,故这种运算被称为蝶形运算。
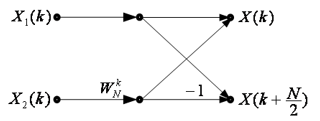
若 N = 2 L N=2^L N=2L,则这个分解可以一只持续下去,直到分解得到的子序列式2点序列为止,易得,两点DFT表示为如下形式
{ X b ( 0 ) = x b ( 0 ) + W 2 0 x b ( 1 ) X b ( 1 ) = x b ( 0 ) − W 2 0 x b ( 1 ) \begin{cases}X_b(0)=x_b(0)+W_2^0x_b(1)\\X_b(1)=x_b(0)-W_2^0x_b(1)\end{cases} {
Xb(0)=xb(0)+W20xb(1)Xb(1)=xb(0)−W20xb(1)
与(3)(4)两式一致,故2点DFT也可化为蝶形运算,于是整个N点DFT可以分解为L级蝶形运算,这样就大大降低了DFT的运算量。

import numpy as np
def dft1d(x):
N=len(x)
x=np.mat(x)
W=np.mat(range(N)).transpose()*np.mat(range(N))
W=np.exp(-2j*np.pi/N*W)
return x*W
def binaryInverse(n,L):
b=bin(n)[2:].zfill(L)
b=b[-1::-1]
return int(b,2)
fftResort=np.frompyfunc(binaryInverse,2,1)
def fft1d(x,oversample=1):
N0=len(x)
N=2**(len(bin(N0-1)[2:]))*2**(oversample-1)
L=len(bin(N0-1)[2:])+oversample-1
x+=[0]*(N-N0)
x=np.array(x,dtype=np.complex)
x=x[np.int16(fftResort(range(N),L))]
for n in range(L):
for k in range(int(2**n)):
W=np.exp(-2j*np.pi/2**(n+1)*k)
x[k::int(2**(n+1))],x[k+int(2**n)::int(2**(n+1))]=\
x[k::int(2**(n+1))]+W*x[k+int(2**n)::int(2**(n+1))],\
x[k::int(2**(n+1))]-W*x[k+int(2**n)::int(2**(n+1))]
return x
2. 快速卷积算法
2.1 基本步骤
快速卷积运算步骤如下:
2.2 运算量
若直接按照 y = ∑ n = 0 M − 1 h ( m ) x ( n − m ) y=\sum\limits_{n=0}^{M-1}h(m)x(n-m) y=n=0∑M−1h(m)x(n−m)计算卷积,则总的乘法次数为
m d = M L … … ( 5 ) m_d=ML……(5) md=ML……(5)
快速卷积运算需要做3次FFT和N次复数乘法,计算量为
m f = N ( 3 2 l o g 2 N + 1 ) … … ( 6 ) m_f=N(\frac{3}{2}log_2N+1)……(6) mf=N(23log2N+1)……(6)
比值为
K m = m d m f = M L N ( 3 2 l o g 2 N + 1 ) = M L ( M + L − 1 ) ( 3 2 l o g 2 ( M + L − 1 ) + 1 ) K_m=\frac{m_d}{m_f}=\frac{ML}{N(\frac{3}{2}log_2N+1)}=\frac{ML}{(M+L-1)(\frac{3}{2}log_2(M+L-1)+1)} Km=mfmd=N(23log2N+1)ML=(M+L−1)(23log2(M+L−1)+1)ML
当 L ≈ M L \approx M L≈M时,
K m ≈ L 3 l o g 2 L + 5 K_m\approx\frac{L}{3log_2L+5} Km≈3log2L+5L
比值随L增加而增大,说明序列越长,快速卷积方法效率越高。
但是当 L > > M L>>M L>>M时
K m ≈ M 3 2 l o g 2 L + 1 K_m\approx\frac{M}{\frac{3}{2}log_2L+1} Km≈23log2L+1M
当L足够大时,快速卷积法反而比直接计算卷积效率低。
2.3 分段卷积
实际信号处理中,序列x(n)的长度大大超过h(n)是很普遍的,为了提高计算效率,应先将序列x(n)分段,使每段长度都与h(n)长度相当,再进行卷积,分段卷积后,还需将卷积结果拼合为长序列的卷积输出,根据分段方式的不同,合成算法也不一样,常用的有重叠相加法和重叠保留法。
2.3.1 重叠相加法

将x(n)分为若干长度为L的子序列,其中每个子序列的表达式为
x i ( n ) = { x ( n + i L ) n = 0 , 1 , . . . , L − 1 0 其 它 … … ( 7 ) x_i(n)=\begin{cases}x(n+iL)&n=0,1,...,L-1\\0&其它\end{cases}……(7) xi(n)={
x(n+iL)0n=0,1,...,L−1其它……(7)
y ( n ) = x ( n ) ∗ h ( n ) = [ ∑ i = 0 ∞ x i ( n − i L ) ] ∗ h ( n ) y(n)=x(n)*h(n)=[\sum\limits_{i=0}^{\infty}x_i(n-iL)]*h(n) y(n)=x(n)∗h(n)=[i=0∑∞xi(n−iL)]∗h(n) = ∑ i = 0 ∞ x i ( n − i L ) ∗ h ( n ) =\sum\limits_{i=0}^{\infty}x_i(n-iL)*h(n) =i=0∑∞xi(n−iL)∗h(n)
由于LSI系统的时不变特性,有
y i ( n − i L ) = x i ( n − i L ) ∗ h ( n ) y_i(n-iL)=x_i(n-iL)*h(n) yi(n−iL)=xi(n−iL)∗h(n)
故
y ( n ) = ∑ i = 0 ∞ y i ( n − i L ) y(n)=\sum\limits_{i=0}^{\infty}y_i(n-iL) y(n)=i=0∑∞yi(n−iL)
在按照(7)式将卷积结果叠加过程中,yi(n)的长度是L+M-1,而每一段的位移是iL,前一段yi-1(n)值的后M-1个样会与后一段yi(n)的前M-1个样值重叠,故这种算法称为重叠相加法。
2.3.2 重叠保留法
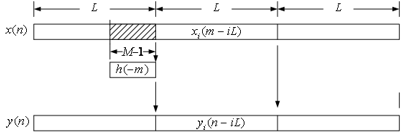
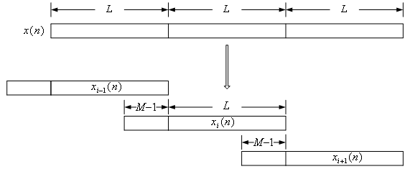
将y(n)均匀分为长度为L没有重叠的子序列,即令
y i ( n ) = { y ( n + i L ) n = 0 , 1 , . . . L − 1 0 其 它 y_i(n)=\begin{cases}y(n+iL)&n=0,1,...L-1\\0&其它\end{cases} yi(n)={
y(n+iL)0n=0,1,...L−1其它
由图可见,yi(n-iL)不仅与第i段输入xi(m-iL)有关,还与前一段的后M-1个值有关,故对x(n)分段时,每一段xi(n)要包含前一段的后M-1个值,分为长度为N=L+M-1相互之间有重叠的子序列xi(n),即
x i ( n ) = { x ( n + i L − M + 1 ) n = 0 , 1 , . . . , N − 1 0 其 它 … … ( 8 ) x_i(n)=\begin{cases}x(n+iL-M+1)&n=0,1,...,N-1\\0&其它\end{cases}……(8) xi(n)={
x(n+iL−M+1)0n=0,1,...,N−1其它……(8)
设xi(n)与h(n)的卷积结果为yi’(n),有由于xi(n)前面增加了M-1个样值,yi’(n)的起始样值与输出分段yi(n)的起始样值不一样,yi(n)应是yi’(n)的第M-1号样值,故
y i ( n ) = y i ′ ( n + M − 1 ) , n = 0 , 1 , . . . , L − 1 y_i(n)=y_{i}^{'}(n+M-1),n=0,1,...,L-1 yi(n)=yi′(n+M−1),n=0,1,...,L−1