FFT快速傅里叶变换

FFT太玄幻了，不过我要先膜拜HQM，实在太强了

1.多项式

1）多项式的定义

在数学中，由若干个单项式相加组成的代数式叫做多项式。多项式中的每个单项式叫做多项式的项，这些单项式中的最高项次数，就是这个多项式的次数。其中多项式中不含字母的项叫做常数项。

2）多项式的表达

我们可以用一些不同的表达方式来表示一个多项式
\[f(x)=\sum_{i=0}^{i=n}a_i\cdot x^i\]

系数表达：

可以用一个n+1维的向量来表示
\[\vec{a}=(a_0,a_1,\cdots,a_n)\]

点值表达：

我们要选取任意\(n+1\)个点值\(x_0,...,x_n\)求出它的\(f(x_i)\),得到\[\{(x_i,f(x_i)):0<=i<=n,i∈Z\} \]
我们可以把\(n\)次多项式\(A(x)\)看作一个函数，那么它可以用平面直角坐标系上的n个点\((x_1,y_1),(x_2,y_2),...,(x_n,y_n)\)来确定。这里我们可以直观理解一下：两个点我们可以轻易确定一条直线，同时我们依然可以由三个点确定一条抛物线，这个是可以证明的，MYH巨佬给我们讲过，但是我太菜了，实在没有听懂。回到上面，我们把这n个点代入\(A(x)\)，我们就可以得到一个\(n\)元一次方程组，然后通过高斯消元就可以确定这个多项式。
系数表达法的多项式乘法时间复杂度显然是\(O(n^2)\)的，但是点值表达法的多项式的乘法的时间复杂度却是\(O(n\))的（两个多项式的每一个点的横坐标都相等）。那我们就会希望可以利用点值表达法的这一优势来快速地进行多项式乘法。但是我们平时使用的都是系数表示法，想要利用这个优势，就要快速地将系数表达法转化为点值表达法。这里我们就要用FFT了。

2.复数

1）复数的定义

我们把形如\(a+bi\)（a,b均为实数）的数称为复数，其中\(a\)称为实部，\(b\)称为虚部，i称为虚数单位，也就是说\(i^2=-1\),或者说\(i=\sqrt{-1}\)。当虚部等于零时，这个复数可以视为实数；当z的虚部不等于零时，实部等于零时，常称z为纯虚数。复数域是实数域的代数闭包，也即任何复系数多项式在复数域中总有根。 复数是由意大利米兰学者卡当在十六世纪首次引入，经过达朗贝尔、棣莫弗、欧拉、高斯等人的工作，此概念逐渐为数学家所接受。

2）复数的四则运算

复数的加法

设\(z_1=a+bi,z_2=c+di\)，那么：\[z_1\pm z_2=(a+c)+(b+d)i\]

复数的乘法

设\(z_1=a+bi,z_2=c+di\)，那么：\[z_1\times z_2=(ac-bd)+(ad+bc)i\]

一个奇奇怪怪的东西

\[e^{i\theta}=cos\theta+isin \theta\]

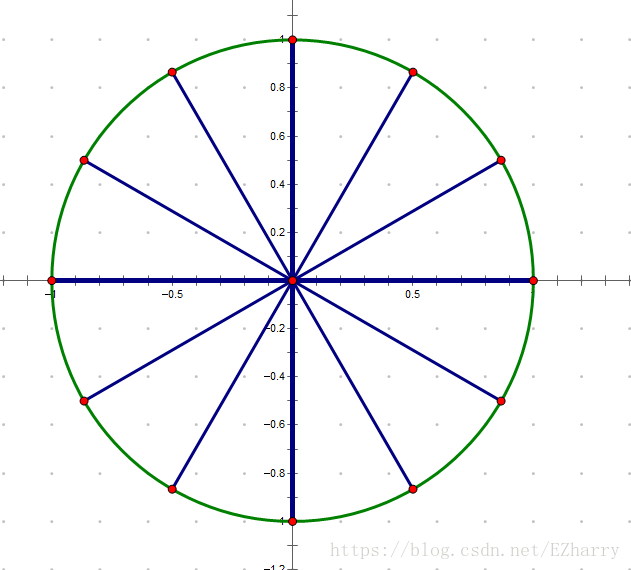
单位复数根

定义

如果\(\omega^n=1\)，那么我们称\(\omega\)为\(n\)次单位根。

单位根的值

事实上，在这里：\[\omega_k=e^\frac{2\pi ik}{n}=cos\frac{2\pi k}{n}+isin\frac{2\pi k}{n}\]
这个可以用欧拉恒等式\((e^{i\pi}+1=0)\)来轻易证明。

消去引理

\[\omega_{dn}^{dk}=\omega_n^k\]
证明：

\[\omega_{dn}^{dk}=(e^\frac{2\pi i}{dn})^{dk}=e^\frac{2\pi ik}{n}=\omega_n^k\]

折半引理

如果n是大于0的一个偶数，那么前\frac{n}{2}个\(n\)次单位根的平方的集合等于后\frac{n}{2}个n次单位根的平方的集合。
证明：对于任意的k<\frac{n}{2}，有：

\[(\omega_n^{k+\frac{n}{2}})^2=\omega_n^{2k+n}=\omega_n^{2k}\omega_n^n=\omega_n^{2k}=(\omega_n^k)^2\]
因此，\[(\omega_n^{k+\frac{n}{2}})^2=(\omega_n^k)^2\]

复数类

struct cmplx{
    double real,imag;
    inline cmplx(double x=0,double y=0){real=x,imag=y;}
    inline cmplx operator +(const int b){return cmplx(real+b,imag);}
    inline cmplx operator -(const int b){return cmplx(real-b,imag);}
    inline cmplx operator *(const int b){return cmplx(real*b,imag*b);}
    inline cmplx operator /(const int b){return cmplx(real/b,imag/b);}
    inline cmplx operator+=(const int b){*this=*this+b;return *this;}
    inline cmplx operator/=(const int b){*this=*this/b;return *this;}
    inline cmplx operator +(const cmplx b){return cmplx(real+b.real,imag+b.imag);}
    inline cmplx operator -(const cmplx b){return cmplx(real-b.real,imag-b.imag);}
    inline cmplx operator *(const cmplx b){return cmplx(real*b.real-imag*b.imag,real*b.imag+imag*b.real);}
    inline cmplx operator+=(const cmplx b){*this=*this+b;return *this;}
    inline cmplx operator*=(const cmplx b){*this=*this*b;return *this;}
};

FFT(fast Fourier transform)

我们正式开始我们的FFT之旅。
FFT就是用来快速求傅里叶变换

证明

终于切入正题了。
DFT就是将一个多项式的系数表达法转化为点值表达法。
具体操作：
对于n-1(2|n)次多项式A(x)，我们有：
\[A(x)=a_0+a_1x+a_2x^2+...+a_{n-1}x^{n-1}\]
令\[A^{[1]}=a_0+a_2x^2+...+a_{n-2}x^{\frac{n}{2}-1}\]
\[A^{[2]}=a_1+a_3x+...+a_{n-1}x^{\frac{n}{2}-1}\]
则\[A(x)=A^{[1]}(x^2)+xA^{[2]}(x^2)\]
把\(\omega_n^k(k<\frac{n}{2})\)代入可得到：\[A(\omega_n^k)=A^{[1]}((\omega_n^k)^2)+\omega_n^kA^{[2]}((\omega_n^k)^2)\]
由折半引理我们会发现\((\omega_n^k)^2=(\omega_n^{k+\frac{n}{2}})^2\)
易证\(\omega_n^k=-\omega_n^{k+\frac{n}{2}}\)
所以\[A(\omega_n^{k+\frac{n}{2}})=A^{[1]}((\omega_n^k)^2)-\omega_n^kA^{[2]}((\omega_n^k)^2)\]
我们会发现这两个式子只有常数项不同
那么当我们在求第一个式子的时候，我们可以直接在O(1)的时间内同时得到第二个式子的值
然后就这样递归下去，就可以得到A(x)的点值表达式了
这里先埋个坑吧，证明真的不想肝啊【绝望脸】
直接上代码吧

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>

using namespace std;

const double pi=acos(-1);

struct cmplx{
    double real,imag;
    inline cmplx(double x=0,double y=0){real=x,imag=y;}
    inline cmplx operator +(const int b){return cmplx(real+b,imag);}
    inline cmplx operator -(const int b){return cmplx(real-b,imag);}
    inline cmplx operator *(const int b){return cmplx(real*b,imag*b);}
    inline cmplx operator /(const int b){return cmplx(real/b,imag/b);}
    inline cmplx operator+=(const int b){*this=*this+b;return *this;}
    inline cmplx operator/=(const int b){*this=*this/b;return *this;}
    inline cmplx operator +(const cmplx b){return cmplx(real+b.real,imag+b.imag);}
    inline cmplx operator -(const cmplx b){return cmplx(real-b.real,imag-b.imag);}
    inline cmplx operator *(const cmplx b){return cmplx(real*b.real-imag*b.imag,real*b.imag+imag*b.real);}
    inline cmplx operator+=(const cmplx b){*this=*this+b;return *this;}
    inline cmplx operator*=(const cmplx b){*this=*this*b;return *this;}
};

cmplx a[10000001],b[10000001];
int n,m,limit,res[10000001];

void fft(cmplx *a,int t){
    for(int i=0;i<n;i++){
        if(i<res[i])swap(a[i],a[res[i]]);
    }
    for(int i=1;i<n;i<<=1){
        cmplx wn(cos(pi/i),t*sin(pi/i));
        for(int p=i<<1,j=0;j<n;j+=p){
            cmplx w(1,0);
            for(int k=0;k<i;k++,w*=wn){
                cmplx x=a[j+k],y=w*a[j+k+i];
                a[j+k]=x+y;a[j+k+i]=x-y;
            }
        }
    }
}

int main(){
    scanf("%d%d",&n,&m);
    for(int i=0;i<=n;i++){
        scanf("%lf",&a[i].real);
    }
    for(int i=0;i<=m;i++){
        scanf("%lf",&b[i].real);
    }
    m+=n;
    for(n=1;n<=m;n<<=1)limit++;
    for(int i=0;i<n;i++){
        res[i]=((res[i>>1]>>1)|(i&1)<<(limit-1));
    }
    fft(a,1);
    fft(b,1);
    for(int i=0;i<=n;i++)a[i]*=b[i];
    fft(a,-1);
    for(int i=0;i<=m;i++){
        printf("%d ",int(a[i].real/n+0.5));
    }
    return 0;
}