快速傅里叶变换（FFT）学习

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/A1847225889/article/details/84887781

首先，在写这篇博客之前，我还没有完全学会FFT。
先把会的部分打好，加深一下记忆（也可以说是做笔记吧）。
初三了，还不会FFT，要退役喽……

---

多项式乘法

点开这篇博客之前，你就应该知道，FFT是用来求多项式乘法的。
什么是多项式，什么是多项式乘法？
不讲。初一内容。
如果要求多项式乘法，有一个非常显然的做法，就是暴力。
时间复杂度是 $O(N^2)$的，很朴素。
然而FFT这个东西可以将其复杂度优化到 $O(N\lg N)$。

---

点值表示法

对s于一个多项式 $A(x)$，最朴素的表示方法长这样：
$A(x)=\sum_{i=0}^n a_i*x^i$
然后，有另一种点值表示法，就是用 $n$个点来表示。
对于一个点 $(x,y)$，可以理解成，将 $x$带入多项式中，求得的结果是 $y$。
其实这 $n$个点不一定是真实存在的，因为在FFT中我们用的是复数……
那么，我们可以通过这 $n$个点的坐标，然后推出原来的式子。
证明？我觉得这个感性理解一下就好了。
可以看作用 $n$个点，定一个 $n$次函数。

然后，对于两个多项式相乘，假设两个点为 $(x,y_1)$和 $(x,y_2)$
那么它们相乘的结果就是 $(x,y_1*y_2)$
这个其实也挺好理解，因为这些多项式可以看成函数。

---

算法的大概流程

一、点值运算

就是将多项式的形式转化成点值表示法。

二、逐项相乘

三、插值运算

将多项式由点值表示法转化回去。

---

$n$次单位根

定义

有一个方程：
$x^n=1$
这个方程，人们看到了，肯定会毫不犹豫地想到 $x=1$。如果 $n$是偶数，还可以是 $-1$。
但是，如果我们把范围延伸到复数，那么，就有 $n$个根。
我们可以画一个图看一下。

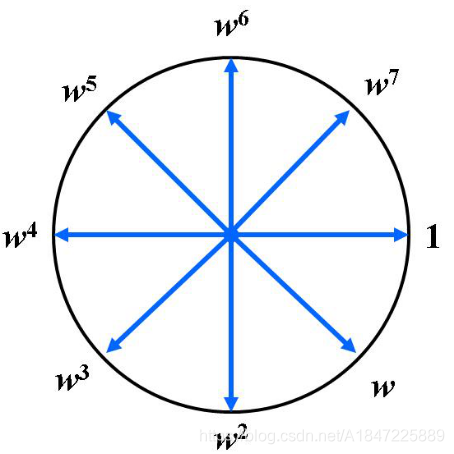
（图片摘自YL的PPT。吐槽一下，为什么和我认识的顺序相反？不过……也没有多大关系，本质上是一样的。）
我们可以发现，这些根围成了一个圆。
这个圆被划分成了 $n$等分。
那么它们究竟是多少呢？

首先，
我说一说复数的乘法：
对于一个复数 $a+bi$，其实有另一种写法： $l(\cos \theta +i\sin \theta)$
这种写法被称为三角表示法，可以用图形理解一下，
$l$叫模长，表示这个点到原点的距离。
$\theta$是原点发出经过它的射线和 $x$洲的正半轴的夹角（逆时针）。
然后，对于两个复数相乘，就相当于是模长相乘，夹角相加。
证明？我不会证。

当初，在某一位大佬讲FFT时，我问怎么证，他简单地化了一下式子，我问最后一步是为什么，怎么证。他说，很简单，用泰勒级数展开就行了。
我：……

总之就这么用就好了。

那么我们可以发现，如果模长都为 $1$，乘起来是不会变的，只是夹角相加。所以有的时候，它会在转若干次的时候转到 $(1,0)$。
所以说，我们可以发现上面的这些点统统可以用 $\omega^k$来表示。
因为它们围成了一个圆，上一个绕着原点转到某一个固定的角度，就得到下一个。从 $(1,0)$开始，转 $n$次，就会回来。
我们记 $\omega_n=\omega_n^1$，为主 $n$次单位根。

性质

1.群的性质 $\omega_n^j\omega_n^k=\omega_n^{(j+k)\mod n}$

这条性质比较显然。因为 $\omega_n^0=\omega_n^n$。
也可以通过图来理解一下。

2.消去引理 $\omega_{dn}^{dk}=\omega_{n}^{k}$

这个东西也可以通过图来理解一下。

3.折半引理 $\omega_n^{k+\frac{n}{2}}=-\omega_n^k$

这个东西还是可以画图理解一下，当然其实也很好证明。
只需要将等式的两边分别平方一下，易得它们的平方相等。
又显然它们不相等（嗯，的确显然）
所以它们一定互为相反数。
好草率的证明啊……

4.求和引理： $n\nmid k$时 $\sum_{j=0}^{n-1}{\left(\omega_n^k\right)}^j=0$，否则 $\sum_{j=0}^{n-1}{\left(\omega_n^k\right)}^j=n$

这个有点复杂，当然，也仅仅是有点复杂……
等比数列求和在复数显然也适用，所以我们直接简单粗暴地强行搬过来：
$\sum_{j=0}^{n-1}{\left(\omega_n^k\right)}^j \\ =\frac{{\left(\omega_n^k\right)}^n-1}{\omega_n^k-1} \\ =\frac{{\left(\omega_n^n\right)}^k-1}{\omega_n^k-1} \\ =0$

用处

用处？
多亏了它奇怪的性质，所以才可以用来玩FFT。
这个性质有什么用，看看后面就知道了。
据说，NTT似乎和FFT的原理差不多，只不过用的是某些模数的特殊性质。所以常数很小。

---

DFT

先不要说FFT，从简单的入手。
之前说过这个东西是用来将普通的性质转换成点值表示法。
我们可以将 $(\omega_n^0,\omega_n^1,......,\omega_n^{n-1})$带入 $A(x)=\sum_{i=0}^{n-1}a_i x^i$，
得到 $(y_0,y_1,......,y_{n-1})$。
显然， $y_k=\sum_{i=0}^{n-1}a_i\omega^{ki}$

IDFT

再讲 $IDFT$
我们现在已经知道了 $A(x)=\sum_{i=0}^{n-1}a_i x^i$的DFT为 $(y_0,y_1,......,y_{n-1})$
我们再设 $B(x)=\sum_{i=0}^{n-1}y_i*x^i$。
我们将 $({\omega_n^0,\omega_{n}^{-1},.....,\omega_{n}^{-(n-1)}})$带入 $B(x)$，又得到一个DFT： $(z_0,z_1,......,z_{n-1})$
然后推一波式子：
$z_k=\sum_{i=0}^{n-1}y_i \left(\omega_n^{-k}\right)^i \\ =\sum_{i=0}^{n-1}\left(\sum_{j=0}^{n-1}a_j \left(\omega_n^i\right)^j\right) \left(\omega_n^{-k}\right)^i\\ =\sum_{j=0}^{n-1} a_j \left(\sum_{i=0}^{n-1}\left(\omega_n^{j-k}\right)^i\right) \\ =n a_k$
其中最后一步用了前面所说的求和引理。
所以 $a_k=\frac{z_k}{n}$
你们现在说，为什么要用这些奇奇怪怪的 $n$次单位根？如果没有这些奇妙的性质，那么在这时候转换就很不方便了。
我们发现，DFT和IDFT的求法实际上是差不多的（可以套用同一个板子），只是要带进去的东西不同。

FFT

其实FFT是DFT的优化。
DFT的时间复杂度是 $O(n^2)$的，很慢（人家傅里叶才懒得帮你算时间复杂度呢！）。
所以我们可以用分治的方法来将其优化到 $O(n\lg n)$
对于一个多项式 $A(x)=\sum_{i=0}^{n-1}a_i x^i$，我们考虑用分治的方式来计算它的DFT。
设 $A_0(x)=a_0+a_2*x+......+a_{n-2}*x^{\frac{n}{2}-1},A_1(x)=a_1+a_3*x+......+a_{n-1}*x^{\frac{n}{2}-1}$
那么我们可以得到 $A(x)=A_0(x^2)+xA_1(x^2)$
设 $k<\frac{n}{2}$，则
$A(\omega_n^k)=A_0(\omega_n^{2k})+\omega_n^k A_1(\omega_n^{2k}) \\ =A_0(\omega_\frac{n}{2}^k)+\omega_n^k A_1(\omega_{\frac{n}{2}}^k) \\ A(\omega_n^{k+\frac{n}{2}})=A_0(\omega_n^{2k+n})+\omega_n^{k+\frac{n}{2}}A_1(\omega_n^{2k+n}) \\ =A_0(\omega_n^{2k})+\omega_n^{k+\frac{n}{2}}A_1(\omega_n^{2k})\\ =A_0(\omega_{\frac{n}{2}}^k)-\omega_n^kA_1(\omega_{\frac{n}{2}}^k)$
我们可以递归地求下去，每次将其分成两半。那么这样子显然是 $O(n \lg n)$的。
（当然，在一开始就要将 $n$补成2次幂的形式，不然会出现不能分成两个相等的部分的尴尬情况。）

FFT的常数优化

如果真的像上面一样递归处理，那就T飞了。
常数太大了啊！
所以说，我们要对它进行优化。

FFT中位置的变换

设一开始的编号为0,1,2,3,4,5,6,7，变换后的编号为0,4,2,6,1,5,3,7
可以将所有的东西用二进制来搞一搞，然后你就会发现：
对应的位置的二进制形式居然是相反的！
是不是很神奇？
接下来我来简略的证明一下（当然还是感性理解）：
每一次将一大块的东西分成两个小块分别处理。
这时候相当于将编号的第 $0$位为 $0$的放左边，为 $1$的放右边。
可以思考一下，如果将这个新的顺序重新编号，那么，左边的最高位都是 $0$，右边的最高位都是 $1$。
所以相当于是最低位和最高位换了一下。
然后再递归向下处理，后面的东西也是一样的。
其实还挺理性的，不是吗？
那么我们可以通过这个结论，来搞一个自底向上的算法，然后就不需要递归，多么舒服！

蝴蝶变换

好高大上的一个名字，是不是？
但实际上，它就是我们再前面讲过的东西：
$A(\omega_n^k) =A_0(\omega_\frac{n}{2}^k)+\omega_n^k A_1(\omega_{\frac{n}{2}}^k) \\ A(\omega_n^{k+\frac{n}{2}}) =A_0(\omega_{\frac{n}{2}}^k)-\omega_n^kA_1(\omega_{\frac{n}{2}}^k)$
可以发现，对于左边的两个东西，转移到它们的两个量是可以一起用的。
如果你画一张图来理解一下，那么你就会发现，这个东西真的很像蝴蝶。
真的好像哟……
这个东西在程序实现的时候直接用上就好了。
在我的印象中，蝴蝶变换本来就是FFT的转移，所以告诉我，为什么还有不用蝴蝶变换的非递归FFT程序？可能是我智商太低，理解不了更差的解法（手动滑稽）。

---

补充

二进制形式相反的怎么弄？

不要想得太多，直接预处理，暴力不会爆炸。
时间复杂度还是一样的……

主 $n$次单位根怎么算？

数形结合……
因为这个半径为 $1$的圆被划成了 $n$等分。
所以每个角就是 $\frac{2\pi}{n}$。
那么 $\omega_n=\cos\frac{2\pi}{n}+i\tan\frac{2\pi}{n}$。
这是一种比较好理解的方法。
但是还有一种很变态，很奇怪，很强大的方法：
$\omega_n=e^{\frac{2\pi i}{n}}$
这是什么鬼？？？
据说脑洞数学家欧拉，他研究出来这么一个玩意： $e^{x i}=\cos x+i\tan x$
所以说 $e^{\frac{2\pi i}{n}}=\cos \frac{2\pi}{n}+i\tan \frac{2\pi}{n}$对吧……
可是原理是什么……还有，如果直接打上这种东西，那么你要用C++自带的<complex>啊！

复数的实现

刚刚还提起过，C++自带了一个叫<complex>的库。
其实自己重载运算符打得更加舒服……吧！
至少我相信手打绝对比自带的快！

注意精度问题

这个不用说了吧……

---

代码实现（易懂&常数大版）

using namespace std;
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#define N 1000000
#define PI 3.14159265358979
struct com{
	double a,b;
	com(double _a=0,double _b=0){a=_a,b=_b;}
};
inline com operator+(const com &x,const com &y){return com(x.a+y.a,x.b+y.b);}
inline com operator-(const com &x,const com &y){return com(x.a-y.a,x.b-y.b);}
inline com operator*(const com &x,const com &y){return com(x.a*y.a-x.b*y.b,x.a*y.b+x.b*y.a);}
inline com operator/(const com &x,const double y){return com(x.a/y,x.b/y);}
int n,m,an,bn;
com a[1<<21],b[1<<21],c[1<<21];
int re[1<<21];
inline void init();
inline void fft(com*,int);
int main(){
	scanf("%d%d",&an,&bn);
	for (int i=0;i<=an;++i){
		int tmp;
		scanf("%d",&tmp);
		a[i]=com(tmp,0);
	}
	for (int i=0;i<=bn;++i){
		int tmp;
		scanf("%d",&tmp);
		b[i]=com(tmp,0);
	}
	for (n=1,m=0;n<=an+bn;n<<=1,m++);//开够足够的n
	init();
	fft(a,1);
	fft(b,1);
	for (int i=0;i<n;++i)
		c[i]=a[i]*b[i];
	fft(c,-1);
	for (int i=0;i<=an+bn;++i)
		printf("%d ",int(c[i].a+0.5));//精度问题……你会发现有一种很尴尬的情况中，输出实数会出现-0
	return 0;
}
inline void init(){//计算每个编号用二进制翻转过来是是什么（想不到什么直接用位运算的巧妙方法）
	for (int i=0;i<n;++i){
		int tmp=0;
		for (int j=0,k=i;j<m;++j,k>>=1)
			tmp=(tmp<<1)+(k&1);
		re[i]=tmp;
	}
}
inline void fft(com* a,int flag){
	for (int i=0;i<n;++i)
		if (i<re[i])
			swap(a[i],a[re[i]]);
	for (int i=1;i<n;i<<=1){//i表示从长度为i的区间转移到长度为i*2的区间
		com wn(cos(flag*PI/i),sin(flag*PI/i));//求主i*2次单位根（注意是i*2次！）
		for (int j=0;j<n;j+=i<<1){//分段来枚举
			com wnk(1,0);
			for (int k=j;k<j+i;++k,wnk=wnk*wn){
				//以下为蝴蝶变换
				com x=a[k],y=wnk*a[k+i];
				a[k]=x+y;
				a[k+i]=x-y;
			}
		}
	}
	if (flag==-1)
		for (int i=0;i<n;++i)
			a[i]=a[i]/n;
}

至于常数小的代码，我真的不会码……
我的这个代码在洛谷的模板题上跑2000+ms，而题目说最好在1000ms以内通过。
审视了半天，没有发现什么优化了之后有特别大的作用的修改方法。
然后，我试着用YL标程里的方法打一遍。YL的标程中FFT的枚举方式和我的不太一样。
我也是着这样打一遍，然后我就发现更慢了……可能是因为他在枚举的过程中没有一个紧接着一个枚举（因为有高速缓存，所以顺序访问数组自然会比跳着访问数组要快）
自己打的程序常数终究是比人家的大啊……

---

参考资料

FFT详解 - 总理同学的编程尝试 - CSDN博客
小学生都能看懂的FFT!!! - 胡小兔 - 博客园