FFT是DFT的改进版,它能快速的(nlogn)在时域与频域间变换。
文文一开始听到什么域什么的,直接就蒙了,后来发现,其实根本不需要去管那个!
我们不需要去管FFT的确切定义,我们只需要知道:它可以快速的求出卷积形式的式子。
什么是卷积形式的额式子呢?就像下面这个!
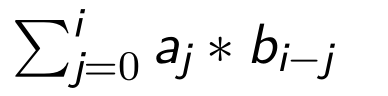
其中,a,b都是数列,求这个式子的值,朴素算法是O(n) 的,我们将这个式子记为Ci 。
我们观察到,对于Ci的计算式中,每一项的A,B的下标之和都相等,都等于i
如果我们想要计算C0~Cn 朴素算法是O(n^2)的。

如果我现在告诉你,我有一种方法,可以在O(nlogn)的时间内,求出C数列,你可能会说:可是这有什么卵用呢?
单独来看,我们很难用到一个形如C这样的数列,但是,我们来看下面这个问题(当然,不是那种直接让你算C数列的裸题)。
给出两个多项式 F(x),G(x),求多项式H(x)=F(x)*G(x)。
我们可以看到,对于两个n次多项式,我们可以得到一个2N次多项式,而第 i 项的系数为……
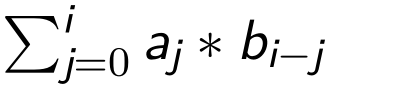 !!!
!!!
是的,就是我们之前遇到的C数组,Ci是第i项的系数,求 H(x) 等价于求C数组的值。
知道了每一项的系数,我们就能轻易的写出H(x).
还记得吗?我之前提到,有一种神奇的算法,可以在O(nlogn)的时间内求出C数列的值。
是的它就是快速傅里叶变换(FFT)。我们之前提到的n^2 实际上是 离散傅里叶变换(DFT)
FFT基于一种分治的思想。
----------------接下来的内容涉及大量数学推导不建议初学者阅读-------------------
--------------------------------建议初学者先掌握用法再了解原理-----------------------
点值表示法:
定理1:对于一个n次多项式,我们可以用n+1的平面上的点唯一确定。
证明1:
任取x0,x1,x2.....xn-1 其中 xi!=xj.
(x0,(f(x0)) (x1,f(x1)) ……称作为f(x)的点值表示
对于一个(xi,yi) 我们有:
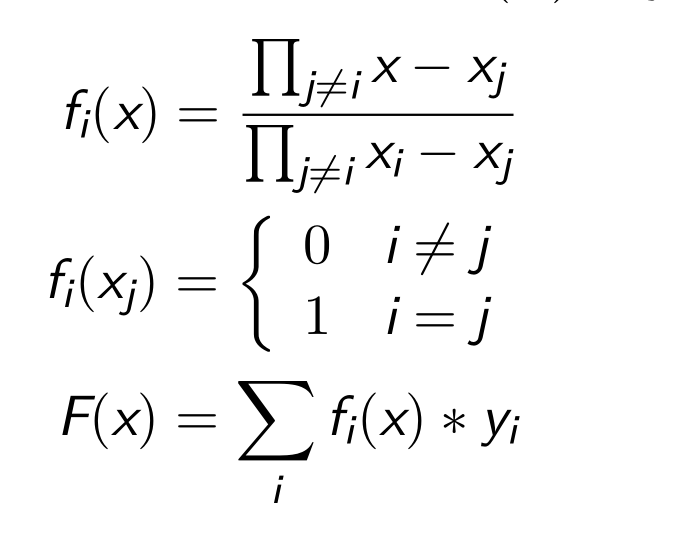
至此,我们计算得到了F(x)各个系数的值,同时唯一确定了这个多项式,定理1得证。
FFT基本思想
通过一组特殊的x,快速求出F(x)的值。
这组数就是单位根。令![]()
![]()
那么,已知ai,![]()
其中,Ai是F(X)各项的系数,从ai转换到bi的过程成为DFT
我们还能得出
定理2:![]()
证明2:
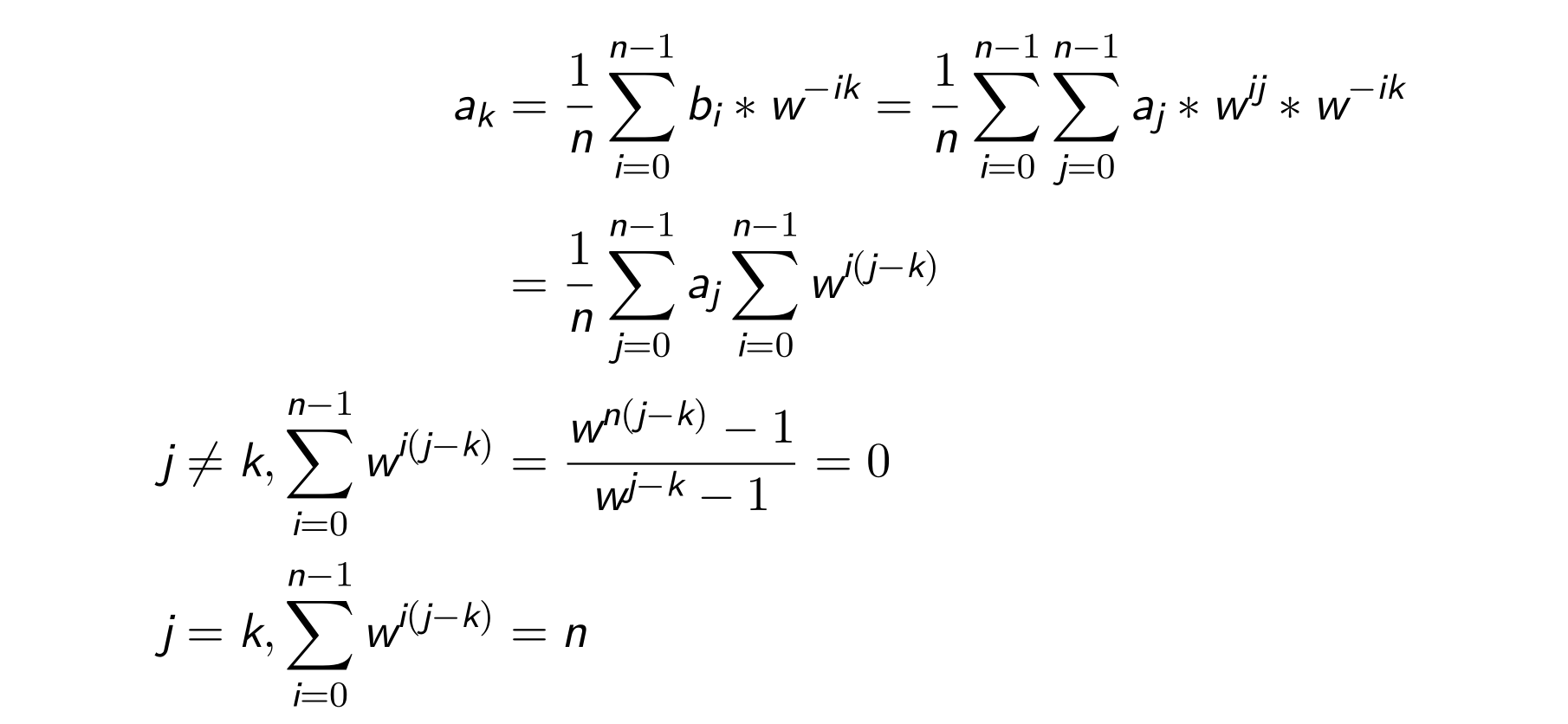
至此,定理2得证
从b转换到a的过程为 IDFT
而FFT就是DFT的快速算法,同时,他还能完成IDFT的工作
我们先说FFT完成DFT工作的过程
先把n补到2的整数幂,不足的部分用0补齐
显然,我们得到 ![]()
我们重新定义两个函数 G(X) h(x) 他们的定义为:
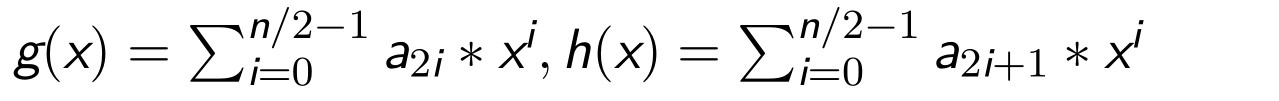
那么,对于F(x)我们就能用G(x) 和H(x)表示出来
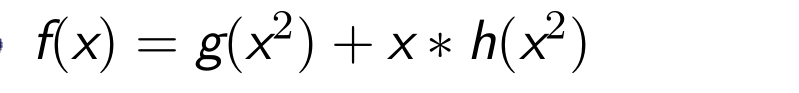
如果已知g(x),h(x)的DFT,既g(w^0),g(w^1)……我们直接带入单位根,就能得到f(x)的值,这让我们想到了什么?分而治之,最后归并。
但是,一个很自然的递归做法,无法大展身手,因为递归版本过于缓慢,不得已,我们将它换成非递归形式。
--------------------------------------------------------------------------------------------------------------------------------------------------------------------------
非递归FFT模版代码(LuoguP3803):

1 #include<cstdio> 2 #include<algorithm> 3 #include<cmath> 4 #include<cstring> 5 const int maxn = 1200000; 6 const double pi = acos(-1.0); 7 struct Complex { 8 double r,i; 9 Complex(double r,double i):r(r),i(i){} 10 Complex(){}; 11 }; 12 Complex operator + (Complex a,Complex b) { 13 return Complex(a.r+b.r,a.i+b.i); 14 } 15 Complex operator - (Complex a,Complex b) { 16 return Complex(a.r-b.r,a.i-b.i); 17 } 18 Complex operator * (Complex a,Complex b) { 19 return Complex(a.r*b.r-a.i*b.i,a.r*b.i+b.r*a.i); 20 } 21 int n,m,L[maxn],R[maxn]; 22 Complex A[maxn<<1],B[maxn<<1]; 23 inline void read(int &x) { 24 char ch=getchar();x=0; 25 while(ch<'0'||ch>'9')ch=getchar(); 26 while(ch>='0'&&ch<='9') {x=(x<<3)+(x<<1)+ch-'0';ch=getchar();} 27 } 28 inline void read(double &x) { 29 char ch=getchar();x=0; 30 while(ch<'0'||ch>'9')ch=getchar(); 31 while(ch>='0'&&ch<='9') {x=10*x+ch-'0';ch=getchar();} 32 } 33 void fft(Complex *a,int n,int inv) { 34 for(register int i=1,j=n/2;i<n-1;++i) { 35 if(i<j) std::swap(a[i],a[j]); 36 int k = n>>1; 37 while(j>=k) { 38 j-=k;k>>=1; 39 } 40 j+=k; 41 } 42 for(register int j=2;j<=n;j<<=1) { 43 Complex wn(cos(2*pi/j*inv),sin(2*pi/j*inv)); 44 for(register int i=0;i<n;i+=j) { 45 Complex w(1,0); 46 for(register int k=i;k<i+(j>>1);k++) { 47 Complex u=a[k],t=a[k+(j>>1)]*w; 48 a[k]=u+t;a[k+(j>>1)]=u-t; 49 w=w*wn; 50 } 51 } 52 } 53 if(inv==-1) for(register int i=0;i<n;i++) a[i].r=a[i].r/n+0.5; 54 } 55 int ans[maxn<<1]; 56 int main() { 57 read(n);read(m); 58 for(register int i=0;i<=n;i++) read(A[i].r); 59 for(register int i=0;i<=m;i++) read(B[i].r); 60 int limit = 1; 61 while(limit<=n+m) limit<<=1; 62 63 fft(A,limit,1);fft(B,limit,1); 64 65 for(register int i=0;i<=limit;i++) { 66 A[i]=A[i]*B[i]; 67 } 68 fft(A,limit,-1); 69 for(register int i=0;i<=m+n;i++) printf("%llu ",(unsigned long long int)(A[i].r)); 70 return 0; 71 }
以及FFT在高精度乘法的应用(LuoguP1919)

1 #include<cstdio> 2 #include<algorithm> 3 #include<cmath> 4 #include<cstring> 5 const int maxn = 1200000; 6 const double pi = acos(-1.0); 7 struct Complex { 8 double r,i; 9 Complex(double r,double i):r(r),i(i){} 10 Complex(){}; 11 }; 12 Complex operator + (Complex a,Complex b) { 13 return Complex(a.r+b.r,a.i+b.i); 14 } 15 Complex operator - (Complex a,Complex b) { 16 return Complex(a.r-b.r,a.i-b.i); 17 } 18 Complex operator * (Complex a,Complex b) { 19 return Complex(a.r*b.r-a.i*b.i,a.r*b.i+b.r*a.i); 20 } 21 int n,m,L[maxn],R[maxn]; 22 Complex A[maxn<<1],B[maxn<<1]; 23 inline void read(int &x) { 24 char ch=getchar();x=0; 25 while(ch<'0'||ch>'9')ch=getchar(); 26 while(ch>='0'&&ch<='9') {x=(x<<3)+(x<<1)+ch-'0';ch=getchar();} 27 } 28 inline void read(double &x) { 29 char ch=getchar();x=0; 30 while(ch<'0'||ch>'9')ch=getchar(); 31 while(ch>='0'&&ch<='9') {x=10*x+ch-'0';ch=getchar();} 32 } 33 void fft(Complex *a,int n,int inv) { 34 for(register int i=1,j=n/2;i<n-1;++i) { 35 if(i<j) std::swap(a[i],a[j]); 36 int k = n>>1; 37 while(j>=k) { 38 j-=k;k>>=1; 39 } 40 j+=k; 41 } 42 for(register int j=2;j<=n;j<<=1) { 43 Complex wn(cos(2*pi/j*inv),sin(2*pi/j*inv)); 44 for(register int i=0;i<n;i+=j) { 45 Complex w(1,0); 46 for(register int k=i;k<i+(j>>1);k++) { 47 Complex u=a[k],t=a[k+(j>>1)]*w; 48 a[k]=u+t;a[k+(j>>1)]=u-t; 49 w=w*wn; 50 } 51 } 52 } 53 if(inv==-1) for(register int i=0;i<n;i++) a[i].r=a[i].r/n+0.5; 54 } 55 int ans[maxn<<1]; 56 char in1[maxn],in2[maxn]; 57 int main() { 58 //freopen("test.in","r",stdin); 59 //freopen("test.out","w",stdout); 60 read(n); 61 scanf("%s%s",in1,in2); 62 int limit = 1; 63 while(limit<=n+n) limit<<=1; 64 for(register int i=n-1;i>=0;i--) 65 A[i].r=(double)(in1[n-i-1]-'0'),B[i].r=(double)(in2[n-i-1]-'0'); 66 fft(A,limit,1);fft(B,limit,1); 67 for(register int i=0;i<=limit;i++) { 68 A[i]=A[i]*B[i]; 69 } 70 fft(A,limit,-1); 71 for(register int i=0;i<=limit;i++) ans[i]=(int)A[i].r; 72 int len = limit; 73 for(register int i=1;i<len;i++) { 74 ans[i]+=ans[i-1]/10;ans[i-1]%=10; 75 } 76 while(ans[len]>=10) { 77 len++; 78 ans[len]=ans[len-1]/10;ans[len-1]%=10; 79 } 80 while(len>=0&&!ans[len]) len--; 81 int least=0; 82 //while(!ans[least]) least++; 83 for(register int i=len;i>=0;i--) { 84 printf("%d",ans[i]); 85 } 86 return 0; 87 }
例题:
BZOJ3527[ZJOI2014] 力 (裸题,考察卷积的定义)
BZOJ3513[MUTC2013]idiots (FFT优化DP)
BZOJ4836[lydsy1704 月赛] 二元运算 (分治FFT 需要较高的技巧)
本三题的题解正在赶制中。。。
