快速傅里叶变换(FFT)学习笔记
快速傅里叶变换(\(\rm Fast\ Fourier\ Transformation\)), 用于在 \(\Theta(n\log n)\) 时间内求两个多项式的乘积.
前置技能
卷积
一个 \(n - 1\) 次 \(n\) 项式 \(f(x)\) 可以表示为 \(f(x) = \sum_0^{n - 1} a_ix^i\).
设有多项式 \(f(x) = \sum_0^{n - 1} a_i x^i\) 和 \(g(x) = \sum_{0}^{n - 1} b_ix^i\), 则有:
\[ f(x) \cdot g(x) = h(x) = \sum_0^{n - 1} a_ix^ig(x) = \sum_0^{n - 1} a_ix^i\left(\sum_0^{n - 1} b_ix^i\right) \]
我们称 \(f(x) \cdot g(x)\) 为 \(f(x)\) 和 \(g(x)\) 的卷积.
复数
定义
定义 \(i = \sqrt{-1}\), 则出现了形如 \(a+bi(a,b\in \mathbb{R})\) 的数.
\(a + bi\) 可以被唯一的表示为复平面上 \((a, b)\) 的点.
复数的模(长):
\(|a + bi| = \sqrt{a^2 + b^2}\).
复数的幅角:
一个复数的幅角为该数在复平面上与实轴的夹角(逆时针), 显然复数的幅角有无穷多个, 若 \(a + bi\) 的幅角 \(\theta\) \(-\pi \le \theta \le \pi\), 则称 \(\theta\) 是 \(a + bi\) 的幅角主值, 记作 \(arg(a + bi)\).
运算
加(减)法:
\((a + bi) + (c + di) = (a + c) + (b + d)i\).
乘法:
\((a + bi)(c + di) = ac + adi + bci - bd = (ac - bd) + (ad + bc)i\).
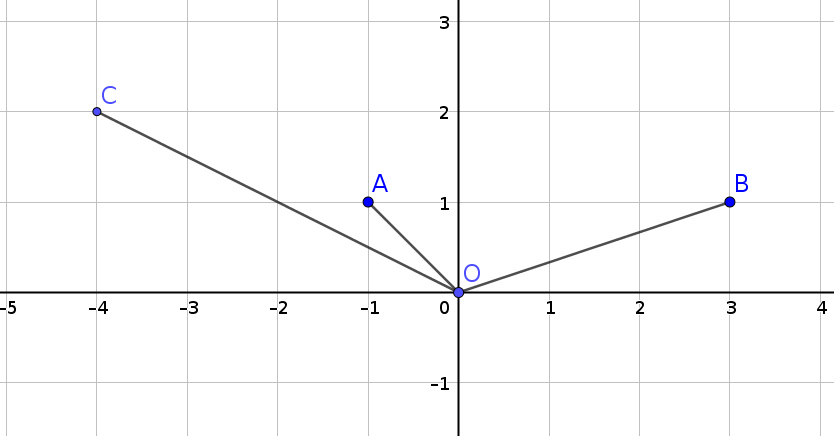
如图, \(A \cdot B = C\), 复数的乘法有以下性质: 模长相乘, 幅角相加.
模长相乘可以以如下方法证明:
设 \(z_1 = a + bi\), \(z_2 = c + di\), \(z_3 = z_1z_2 = (ac - bd) + (ad + bc) i\);
有:
\(|z_1|\cdot |z_2| = \sqrt{a^2 + b^2}\cdot \sqrt{c^2 + d^2} = \sqrt{(a^2 + b^2)(c^2 + d^2)} = \sqrt{a^2c^2 + a^2d^2 + b^2c^2 + b^2d^2}\)
\(|z_3| = \sqrt{(ac - bd) ^ 2 + (ad + bc) ^ 2} = \sqrt{a^2c^2 + a^2d^2 + b^2c^2 + b^2d^2} = |z_1|\cdot |z_2|\)
共轭:
\(\overline{a + bi} = a - bi\), 易证任何复数乘上它的共轭都为实数, \((a + bi)(a - bi) = a ^ 2 + b ^2\).
除法:
\[ \frac{a + bi}{c + di} = \frac{(a + bi)(c - di)}{c^2 + d^2} = \frac{ac + bd}{c^2 + d^2} + \frac{ad + bc}{c^2 + d^2}i \]
单位根
定义 \(n(n\ge 1)\) 次单位根的 \(n\) 次幂等于 \(1\).
显然单位根的模长等于 \(1\), 否则怎么乘都不会是 \(1\).
所以, 单位根都在单位圆上.
考虑设单位根幅角为 \(\alpha\), 则有 \(n\alpha = 2k\pi, (k\in \mathbb N)\).
解得:
\[ \alpha = \frac{2k\pi}{n} = \frac{2\pi}{n}k \]
所以, 单位根 \(n\) 等分单位圆.
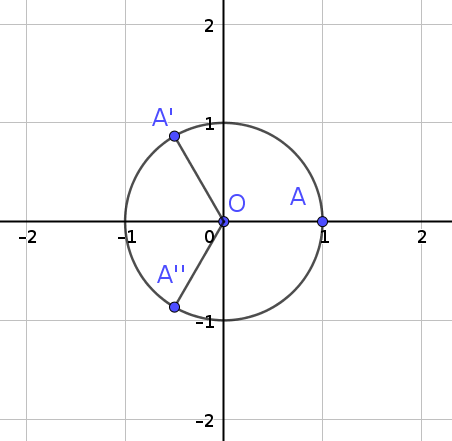
注意到, 当 \(k = n\) 时, 进入了循环, 所以只有 \(n\) 个单位根.
对于 \(n\) 次的幅角为 \(\frac{2\pi}{n}k\) 的单位根我们记作 \(\omega_n^k\).
显然, \(\omega_n^k = \omega_n^{k\% n}\).
得到幅角 \(\alpha\) 后, 我们可以很轻易的得到该单位根所对应的数.
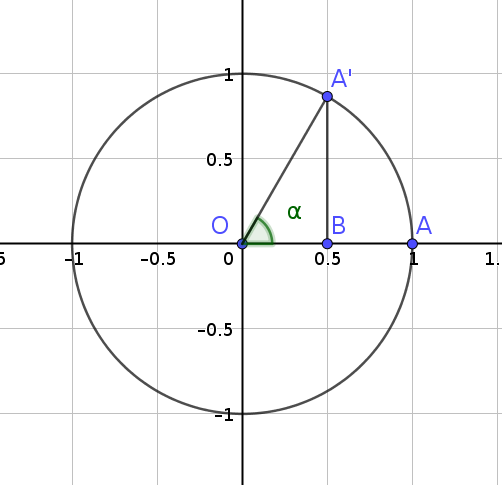
如上图, \(A'B = OA \cdot \sin \alpha = \sin \alpha\);
\(OB = OA \cdot \cos \alpha = \cos \alpha\).
所以点 \(A'\) 所代表的数为 \(\cos \alpha + i\sin \alpha\).
所以
\[ \begin{array}{} \omega_n^k & = \cos \frac{2\pi}{n}k + i\sin \frac{2\pi}{n}k \\ & = e^{i\frac{2\pi}{n}k} = \left(e^{i\frac{2\pi}{n}}\right)^k \\ & = (\omega_n^1)^k \end{array} \]
由上式, 有:
\(\omega_n^j\omega_n^k = (\omega_n^1)^j(\omega_n^1)^k = (\omega_n^1)^{j + k} =\omega_n^{j + k}\);
同上, 显然有 \((\omega_n^j)^k = (\omega_n^k)^j\);
\(\omega_{dn}^{dk} = e^{i\frac{2\pi}{dn}dk} = e^{i\frac{2\pi}{n}k} = \omega_n^k\);
所以 \(\omega_{2n}^n = \omega_2^1 = -1\);
\(\omega_{2n}^{k + n} = \omega_{2n}^k\omega_{2n}^n = -\omega_{2n}^k\);