FFT - 快速傅里叶变换

给出一个\(n\)次多项式\(F(x)\)，和一个\(m\)次多项式\(G(x)\)

求出$F(x) \(和\)G(x)$的卷积

暴力

void solve(){
    for(int i = 0; i <= n; i++)
        for(int j = 0; j <= m; j++)
            c[i + j] += a[i] * b[j];
}

多项式

系数表示法

\(f(x) = \{a_0,a_1,a_2,\dots ,a_{n - 1}\}\)

点值表示法

把多项式放到平面直角坐标系里，看成一个函数

把\(n\)个不同的\(x\)带入，得到唯一确定的\(y\)，就有\(n\)个不同的点

\(f(x) = \{(x_0,f(x_0)), (x_1,f(x_1)),\dots, (x_{n - 1}, f(x_{n - 1}))\}\)

设\(f(x) = \{(x_0,f(x_0)), (x_1,f(x_1)),\dots , (x_{n},f(x_{n}))\}\)

设\(g(x) = \{(x_0,f(x_0)),(x_1,f(x_1)),\dots,(x_{n},f(x_n))\}\)

那么\(f(x)g(x) = \{(x_0,f(x_0)⋅g(x_0)),(x_1,f(x_1)⋅g(x_1)),\dots,(x_n,f(x_n)⋅g(x_n))\}\)

复数

设\(z_1 = a + bi, z_2 = c + di\)

\[z_1 + z_2 = (a + c) + (b + d)i\\ z_1z_2 = (ac - bd) + (ad + bc)i \]

DFT(离散傅里叶变换)

考虑将一个\(n\)项\((n = 2^k)\)的多项式\(A(x)\)，将其系数表达式转换为点值表达式，求出每一个点值的过程

把一个单位圆进行n等分，编号为从0开始逆时针编号

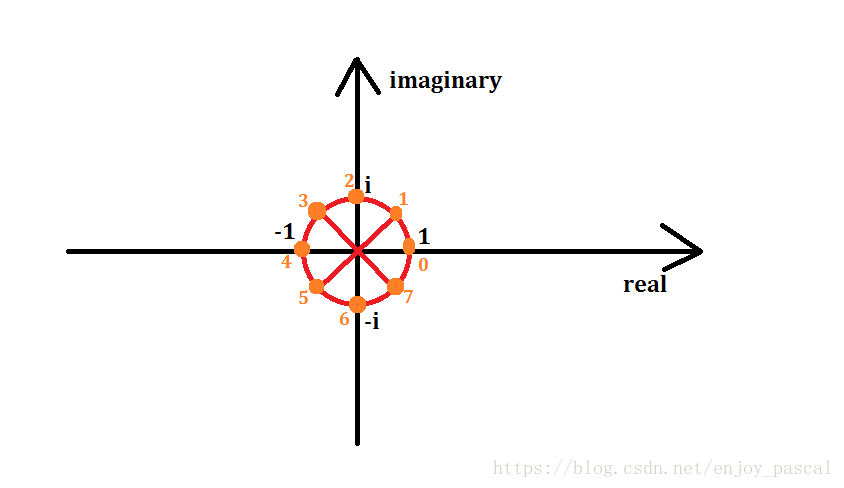
记编号为\(k\)的点代表的复数值为\(w_n^k\)，因为模长相同，极角相加可知\((\omega_n^1)^k = \omega_n^k\)

\[\omega_{n}^{k}=\cos \left(2 \pi \cdot \frac{k}{n}\right)+i \cdot \sin \left(2 \pi \cdot \frac{k}{n}\right) \]

那么\(\omega_n^0,\omega_n^1,\dots, \omega_n^{n-1}\)就是要带入的\(x_0,x_1,\dots ,x_{n - 1}\)

单位根性质

1. \(\omega_n ^k = \omega_{2n}^{2k}\)
2. \(\omega_n^{k + \frac{n}{2}} = -\omega_n^k\)
3. \(\omega_n^0 = \omega_n^n = 1 + 0i\)
4. \((\omega_n^k)^2 = \omega_n^{2k}\)

DFT

利用DFT来分治求

对于一个多项式\(A(x) = \sum_{i = 0}^{n - 1}a_ix^i\)

按照\(A(x)\)下标的奇偶性把\(A(x)\)分成两半

\[A(x)= （a_0 + a_2x^2 + \dots + a_{n - 2}x^{n - 2}） + (a_1x+a_3x^3 + \dots + a_{n - 2}x^{n - 2})\\=(a_0 + a_2x^2 + \dots + a_{n - 2}x^{n - 2}) + x(a_1 + a_3x^2 +\dots + a_{n - 1}x^{n - 2}) \]

设多项式\(A_1(x),A_2(x)\)

\[A_1(x)= a_0 + a_2x + a_4x^2 + \dots + a_{n - 2}x^{\frac{n}{2} - 1}\\ A_2(x)= a_1 + a_3x + a_5x^2 + \dots + a_{n - 1}x^{\frac{n}{2} - 1} \]

满足\(A(x) = A_1(x^2) + xA_2(x^2)\)

设\(k < \frac{n}{2}\)，把\(\omega_n^k\)作为\(x\)带入\(A(x)\)

\[A(\omega_n^k)= A_1((\omega_n^k)^2) + \omega_n^kA_2((\omega_n^k)^2)\\ =A_1(\omega_n^{2k}) + \omega_n^kA_2(\omega_n^{2k}) \\ =A_1(\omega_{\frac{n}{2}}^k) + \omega_n^kA_2(w_{\frac{n}{2}}^k) \]

那么对于那对于\(k ≥\frac{n}{2}\)的情况，令$k = \frac{n}{2} + k, k<\frac{k}{2} \(即\)A(\omega_n^{k + \frac{n}{2}})$，有

\[A(\omega_n^{k + \frac{n}{2}})=A_1(\omega_n^{2k + n}) + \omega_n^{k + \frac{n}{2}} A_2(\omega_n^{2k + n}) \\ = A_1(\omega_n^{2k}\omega_n^n) - \omega_n^kA_2(\omega_n^{2k}\omega_n^n)\\ = A_1(\omega_n^{2k}) - \omega_n^kA_2(w_n^{2k}) \\ = A_1(w_{\frac{n}{2}}^k) - w_n^kA_2(\omega_{\frac{n}{2}}^k) \]

发现\(A(\omega_n^k)\)和\(A(\omega_n^{k + \frac{n}{2}})\)两个多项式只有后面的符号不同

也就是说，如果知道了\(A_1(\omega_{\frac{n}{2}}^k)\)和\(A_2(\omega_{\frac{n}{2}}^k)\)，就可以同时知道\(A(\omega_n^k)\)和\(A(\omega_n^{k + \frac{n}{2}})\)

那么就可以递归分治来求得每一个\(A(x)\)

时间复杂度\(O(nlogn)\)

离散傅里叶反变换

利用快速傅里叶变换将点值表达式的多项式转换为系数表示的过程

把DFT的\(\omega_n\)都取复数(共轭复数)，最后除以\(n\)即可

代码

递归版

#include <iostream>
#include <cstdio>
#include <complex>
using namespace std;
const double Pi = acos(-1);
const int N = 4e6 + 5;
complex<double> f[N], g[N];
void FFT(complex<double> *a, int n, int inv){
    if(n == 1)return;
    complex<double> a1[n >> 1], a2[n >> 1];
    for(int i = 0; i < n ; i += 2)
        a1[i >> 1] = a[i], a2[i >> 1] = a[i + 1];
    FFT(a1, n >> 1, inv); FFT(a2, n >> 1, inv);
    complex<double> x(cos(2 * Pi / n), sin(2 * Pi / n) * inv), w(1, 0);
    for(int i = 0; i < (n >> 1); i++, w *= x)
        a[i] = a1[i] + w * a2[i], a[i + (n >> 1)] = a1[i] - w * a2[i];
}
int main(){
    int n, m, x;
    scanf("%d%d", &n, &m);
    for(int i = 0; i <= n; i++){
        scanf("%d", &x), f[i].real(x);
    }
    for(int i = 0; i <= m; i++){
        scanf("%d", &x), g[i].real(x);
    }
    for(m += n, n = 1; n <= m; n <<= 1);
    FFT(f, n, 1); FFT(g, n, 1);
    for(int i = 0; i < n; i++)
        f[i] *= g[i];
    FFT(f, n, -1);
    for(int i = 0; i <= m; i++)
        printf("%d ", int(0.5 + f[i].real() / n));
    return 0;
}

发现递归版每次都需要开辟一个数组，而且值还需要重新赋值

迭代版

假设数组\(a\)已经变成了第四层，那么先对\(a_0\)和\(a_4\)，\(a_4\)和\(a_2\)，\(a_2\)和\(a_6\)，\(a_6\)和\(a_1\)，\(a_1\)和\(a_5\)，\(a_5\)和\(a_3\)，\(a_3\)和\(a_7\)进行蝴蝶操作，变成第三层，依次类推

那么问题就是把初始化数组变成最后一层，

考虑二进制形式000,100,010,110,001,101,011,111和原数组000,001,010,011,100,101,110,111就是二进制的每个位置的反过来

#include <cstdio>
#include <iostream>
#include <complex>
#include <cmath>
using namespace std;
const int N = 3e6 + 1;
const double Pi = acos(-1);
int n, m, r[N];
complex<double> F[N], G[N];
int getint() {
    int x = 0, f = 1; char c = getchar();
    while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
    while(c >= '0' && c <= '9') x = (x << 1) + (x << 3) + c - '0', c = getchar();
    return x * f;
}
void FFT(complex<double> *a, int n, int inv){
    for(int i = 0; i < n; i++)
        if(r[i] > i) swap(a[r[i]], a[i]);

   for(int mid = 2; mid <= n; mid <<= 1){
        complex<double> x(cos(2 * Pi / mid), inv * sin(2 * Pi / mid));
        for(int i = 0; i < n; i += mid){
            complex<double> w(1,0);
            for(int j = i; j < i + (mid >> 1); j++, w *= x){
                complex<double> t1 = a[j],t2 = a[j + (mid >> 1)] * w;
                a[j] = t1 + t2; a[j + (mid >> 1)] = t1 - t2;
            }
        }
    }
}
int main(){
    scanf("%d %d", &n, &m);
    for(int i = 0; i <= n; i++) F[i].real(getint());
    for(int i = 0; i <= m; i++) G[i].real(getint());
    int l = 0;
    for(m += n, n = 1; n <= m; n *= 2, l++);
    for(int i = 0; i < n; i++)
        r[i] = (r[i >> 1] >> 1) | ((i & 1) << (l - 1));
    FFT(F, n, 1); FFT(G, n, 1);
    for(int i = 0; i < n; i++) F[i] = F[i] * G[i];
    FFT(F, n, -1);
    for(int i = 0; i <= m; i++)
        printf("%d ", (int)(F[i].real() / n + 0.5));
    return 0;
}

FFT求大整数乘法

看成一个多项式\(a_0 + a_1 \times 10 + a_2 \times 10^2 + \dots +a_{n}\times 10^n\)

#include <cstdio>
#include <iostream>
#include <complex>
#include <cmath>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 2e6 + 1;
const double Pi = acos(-1);
int n, m, r[N];
complex<double> F[N], G[N];
void FFT(complex<double> *a, int n, int inv){
    for(int i = 0; i < n; i++)
        if(r[i] > i) swap(a[r[i]], a[i]);

   for(int mid = 2; mid <= n; mid <<= 1){
        complex<double> x(cos(2 * Pi / mid), inv * sin(2 * Pi / mid));
        for(int i = 0; i < n; i += mid){
            complex<double> w(1,0);
            for(int j = i; j < i + (mid >> 1); j++, w *= x){
                complex<double> t1 = a[j],t2 = a[j + (mid >> 1)] * w;
                a[j] = t1 + t2; a[j + (mid >> 1)] = t1 - t2;
            }
        }
    }
}
void solve(){
    int l = 0;
    for(m += n, n = 1; n <= m; n *= 2, l++);
    for(int i = 0; i < n; i++)
        r[i] = (r[i >> 1] >> 1) | ((i & 1) << (l - 1));
    FFT(F, n, 1); FFT(G, n, 1);
    for(int i = 0; i < n; i++)F[i] = F[i] * G[i];
    FFT(F, n, -1);

    int dig = 0;
    char s[N];
    for(int i = 0; i <= m; i++){
        int x = (int)(F[i].real() / n + 0.5) + dig;
        dig = x / 10; x %= 10;
        s[i] = '0' + x;
    }
    while(dig){
        s[++m] = dig % 10 + '0';
        dig /= 10;
    }
    s[++m] = '\0';
    reverse(s, s + m);
    printf("%s\n", s);
}
int main(){
    char s[N];
    scanf("%s", s);
    n = strlen(s) - 1;
    for(int i = 0; i <= n; i++)F[i].real(s[n - i] - '0'); 
    scanf("%s", s);
    m = strlen(s) - 1;
    for(int i = 0; i <= m; i++)G[i].real(s[m - i] - '0');
    solve();
    return 0;
}